LabLynx Wiki

En ljuskon är den sträcka som en blixt av ljus, som härrör från en enskild händelse E (lokaliserad till en enda punkt i rummet och en enda tidpunkt) och färdas åt alla håll, skulle ta genom rumtiden.

Om man föreställer sig ljuset begränsat till ett tvådimensionellt plan sprids ljuset från blixten ut i en cirkel efter att händelsen E inträffar, och om vi plottar den växande cirkeln med den vertikala axeln på grafen som representerar tid, blir resultatet en kon, känd som den framtida ljuskonen. Den förflutna ljuskäglan beter sig som den framtida ljuskäglan men omvänt, en cirkel som drar ihop sig i radie med ljusets hastighet tills den konvergerar till en punkt vid den exakta positionen och tiden för händelsen E. I verkligheten finns det tre rymddimensioner, så ljuset skulle faktiskt bilda en expanderande eller sammandragande sfär i tredimensionell (3D) rymd snarare än en cirkel i 2D, och ljuskäglan skulle faktiskt vara en fyrdimensionell version av en kon vars tvärsnitt bildar 3D-sfärer (analogt med en normal tredimensionell kon vars tvärsnitt bildar 2D-cirklar), men konceptet är lättare att visualisera med antalet rumsliga dimensioner reducerat från tre till två.

Denna syn på speciell relativitet föreslogs först av Albert Einsteins tidigare professor Hermann Minkowski och är känd som Minkowski-rymden. Syftet var att skapa en invariant rumtid för alla observatörer. För att upprätthålla kausalitet begränsade Minkowski rumtiden till icke-euklidisk hyperbolisk geometri.^[1]

Eftersom signaler och andra kausala influenser inte kan färdas snabbare än ljus (se speciell relativitet), spelar ljuskäglan en väsentlig roll för att definiera begreppet kausalitet. För en given händelse E skulle uppsättningen av händelser som ligger på eller inuti den tidigare ljuskonen av E också vara uppsättningen av alla händelser som skulle kunna skicka en signal som skulle hinna nå E och påverka den på något sätt. Till exempel, vid en tidpunkt tio år före E, om vi betraktar mängden av alla händelser i den tidigare ljuskonen av E som inträffade vid den tiden, skulle resultatet bli en sfär (2D:skiva) med en radie på tio ljus-år centrerat på den position där E kommer att inträffa. Så, vilken punkt som helst på eller inuti sfären skulle kunna skicka en signal som rör sig med ljusets hastighet eller långsammare som skulle hinna påverka händelsen E, medan punkter utanför sfären i det ögonblicket inte skulle kunna ha något kausalt inflytande på E. På samma sätt skulle uppsättningen av händelser som ligger på eller inne i framtidenljuskonen av E också vara uppsättningen av händelser som skulle kunna ta emot en signal som skickas ut från positionen och tiden för E, så den framtida ljuskonen innehåller alla händelser som potentiellt kan vara orsaksmässigt påverkade av E. Händelser som inte ligger någondera i tidigare eller framtida ljuskon av E kan inte påverka eller påverkas av E i relativitet.^[2]

I speciell relativitetsteori är en ljuskon (eller nollkon) ytan som beskriver den tidsmässiga utvecklingen av en ljusblixt i Minkowskis rumtid. Detta kan visualiseras i 3-rum om de två horisontella axlarna väljs att vara rumsliga dimensioner, medan den vertikala axeln är tid.^[3]

Ljuskonen är konstruerad enligt följande. Om man som händelse p tar en ljusblixt (ljuspuls) vid tidpunkten t₀, bildar alla händelser som kan nås av denna puls från p den framtida ljuskonen av p, medan de händelser som kan skicka en ljuspuls till p bildar det förflutna ljuskon av p.

Givet en händelse E klassificerar ljuskonen alla händelser i rumtiden i 5 distinkta kategorier:

• Händelser på den framtida ljuskonen av' 'E.
• Händelser på den förflutna ljuskonen av E.
• Händelser inuti den framtida ljuskonen av E är de som påverkas av en materialpartikel som emitteras vid E.
• Händelser inuti den tidigare ljuskonen av E är de som kan avge en materialpartikel och påverka vad som händer vid E.
• Alla andra händelser är i (absolut) någon annanstans i E och är sådana som inte kan påverka eller påverkas av E.

Ovanstående klassificeringar gäller i alla referensramar, det vill säga en händelse som bedöms vara i ljuskonen av en observatör, kommer också att bedömas vara i samma ljuskon av alla andra observatörer, oavsett deras referensram. Det är därför konceptet är så kraftfullt.

Ovanstående hänvisar till en händelse som inträffar på en specifik plats och vid en specifik tidpunkt. Att säga att en händelse inte kan påverka en annan betyder att ljus inte kan komma från platsen för den ena till den andra under en viss tid. Ljus från varje händelse kommer i slutändan att ta sig till den tidigare platsen för den andra, men efter att dessa händelser har inträffat.

Allt eftersom tiden fortskrider kommer den framtida ljuskäglan för en given händelse så småningom att växa till att omfatta fler och fler platser (med andra ord, 3D-sfären som representerar tvärsnittet av 4D-ljuskonen vid ett visst ögonblick blir större senare gånger). Men om vi föreställer oss löptid bakåt från en given händelse, skulle händelsens tidigare ljuskon också omfatta fler och fler platser vid tidigare och tidigare tidpunkter. De längre platserna kommer att vara vid senare tidpunkter. Om vi till exempel betraktar den tidigare ljuskonen av en händelse som äger rum på jorden idag, skulle en stjärna 10 000 ljusår bort bara vara inuti den tidigare ljuskonen vid tidpunkter 10 000 år eller tidigare. Den tidigare ljuskäglan av en händelse på dagens jord, vid dess yttersta kanter, inkluderar mycket avlägsna objekt (varje objekt i observerbart universum), men bara som de såg ut för länge sedan, när universum var ungt.

Två händelser på olika platser, samtidigt (enligt en specifik referensram), är alltid utanför varandras tidigare och framtida ljuskoner, ljus kan inte färdas ögonblickligen. Andra observatörer kan se händelserna inträffa vid olika tidpunkter och på olika platser, men på ett eller annat sätt kommer de två händelserna också att ses vara utanför varandras koner.

Om man använder ett system av enheter där ljusets hastighet i vakuum definieras som exakt 1, till exempel om rymden mäts i ljussekunder och tiden mäts i sekunder, då, förutsatt att tidsaxeln är ritad ortogonalt mot de rumsliga axlarna, när konen delar tids- och rymdaxlarna i två delar kommer den att visa en lutning på 45°, eftersom ljus färdas en sträcka på en ljussekund i vakuum under en sekund. Eftersom speciell relativitetsteori kräver att ljusets hastighet är lika i varje tröghetsram, måste alla observatörer anlända till samma vinkel på 45° för sina ljuskoner. Vanligtvis används ett Minkowski-diagram för att illustrera denna egenskap hos Lorentztransformationer. På andra ställen är en integrerad del av ljuskoner området av rumtiden utanför ljuskonen vid en given händelse (en punkt i rumtiden). Händelser som är någon annanstans från varandra är ömsesidigt oobserverbara och kan inte kopplas samman.

(Figuren på 45° har egentligen bara betydelse i rymd-rymd, eftersom vi försöker förstå rum-tid genom att göra rymd-rymd-ritningar. Rum-rymd-lutning mäts med vinklar, och beräknas med trignometriska funktioner. Rum-tid-lutning mäts med snabbhet och beräknad med hyperboliska funktioner.)

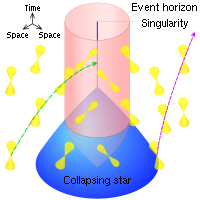
I platt rumtid är den framtida ljuskonen för en händelse gränsen för dess kausala framtid och dess tidigare ljuskon är gränsen för dess kausala förflutna.

I en krökt rumtid, förutsatt att den är globalt hyperbolisk, är det fortfarande sant att en händelses framtida ljuskon inkluderar gränsen för dess kausala framtid (och på liknande sätt för det förflutna). Emellertid kan gravitationslinser få en del av ljuskäglan att vikas in på sig själv, på ett sådant sätt att en del av konen är strikt innanför den kausala framtiden (eller det förflutna), och inte på gränsen.

Ljuskoner kan inte heller alla lutas så att de är "parallella". Detta återspeglar det faktum att rumtiden är krökt och är väsentligt annorlunda från Minkowskis rymd. I vakuumregioner (dessa punkter i rumtiden som är fria från materia), reflekteras denna oförmåga att luta alla ljuskoner så att de alla är parallella i att Weyl-tensorn inte försvinner.

• Lorentztransformation
• Vågekvation

Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Light cone, 10 mars 2023.

• Wikimedia Commons har media som rör ljuskon.
• The Paradox of Special Relativity