Clinfowiki

Posted on July 23, 2020 By Robert Payne

Precesija zvrka ili žiroskopa.[1][2][3]
Zemljina precesija.[4]
Nebeski svod se kreće po krivој, koja je rezultanta uzajamnog delovanja rotacije (zeleno), precesije (plavo) i nutacije (crveno).
Položaj proletne tаčke danas (2014.) i pre, za razdoblje od 6 milenijuma.
Пројекција преспецијалне стазе Северног пола на фиксном небу Епоха Ј2000.0 за временски интервал од 48000 пре заједничке ере до 52000 уобичајене ере.[5]

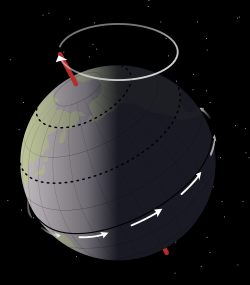
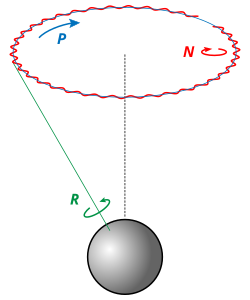
Precesija (kasnolatinski praecessio, prema klasičnom latinskom praecedere: ići napred) je pravilna promena smera ose rotirajućeg tela koja nastaje kada na telo deluje spoljašnji moment sile.[6] Promena ugaone količine kretanja ima smer momenta sile i vektorski se sabira s trenutnom ugaonom količinom kretanja. Pojava je opažena pri kretanju žiroskopa učvršćenog u jednoj tački ose izvan težišta. Precesija nebeskog tela nastaje ako ono nije homogena kugla i ako na njega gravitacijski deluje drugo telo koje se ne nalazi u ravni nebeskog ekvatora.

Zemljina precesija nastaje pod delovanjem Sunca i Meseca. Zbog Zemljine protežnosti javlja se razlika privlačne sile Meseca ili Sunca na bližoj i daljoj strani Zemlje, a kako ta razlika ima komponentu u smeru normalnom na ekvatorsku ravan rotirajuće Zemlje, nastaje spreg sila, odnosno rezultantni moment sile. Zbog toga osa Zemljine vrtnje opisuje kupu oko normale na spojnicu središta Zemlje i Meseca, odnosno Zemlje i Sunca. To je luni-solarna precesija.[7] Kako se Mesec ne nalazi u ravni ekliptike, već mu se od nje staza zakošena za ugao od 5° 9′, na kupi se javljaju nabori s periodom od 18,67 godina, što se u astronomiji naziva nutacijom. Postoji i planetarna precesija, koja je zakretanje ravni ekliptike zbog uticaja planeta.[8] Zbirni učinak luni-solarne i planetarne precesije uzrokuje pomak proletne i jesenske tačke među zvezdama na zapad, godišnje za 50,6′′. Zbog precesije Zemljina osa obilazi oko normale na ravani ekliptike sa sideričkim ili zvezdanim periodom od 25.800 godina (Platonova godina).[9] Posledica toga je da Severni nebeski pol putuje među zvezdama; na mestu gde je danas Severnjača, zvezde se izmenjuju. Zbog precesije Zemljina siderička (zvezdana) i tropska (Sunčeva) godina nisu jednake, a koordinate ekvatorskog koordinatnog sistema se menjaju.[10]

Važna posledica precesije je različito izlaganje Zemljinih kontinenata Sunčevom zračenju. Za klimatske promene važniji je položaj Zemljine ose prema perihelu Zemljine staze nego prema zvezdama, a perihel se zbog poremećaja u Sunčevom sistemu zakreće direktno (progradno), godišnje za 11,63′′, tj. Zemljina se eliptična putanja zakreće. Precesijsko-perihelni ciklus traje 21.000 godina.[11]

Zemljina precesija i nutacija

Osim vrtnje (rotacije) i obilaženja oko Sunca (revolucije), Zemlja pokazuje još jednu vrstu kretanja. Njena osa takođe se neprestano kreće i opisuje kupu oko pola ekliptike, i to u smislu levog vijka koji napreduje na sever. Vršni poluugao kupe jednak je nagibu ekliptike (ekliptika je nagnuta pod uglom od 23°27′ prema nebeskom ekvatoru).[12] Zbog toga zakretanja ose u istom se smislu zakreće i presecište ravni ekliptike s nebeskim ekvatorom, a sa njime i proletna tačka. Zato proletna tačka menja mesto među zvezdama. Pomak proletne tačke odvija se u smeru dnevne vrtnje neba, a to je upravo suprotno od prividnog, godišnjeg kretanja Sunca: proletna tačka se kreće na zapad, a Sunce na istok. To znači da proletna tačka ide u susret Suncu, ili „pred” Sunce. Otuda potiče latinski naziv te pojave, jer praecedere znači ići napred.

Zemljinu precesiju tumači mehanika rotirajućeg krutog tela. Najjači uticaj na nju pokazuju Mesec i Sunce. Mesec je delotvorniji zato što je mnogo bliže. Zajednički učinak Meseca i Sunca naziva se luni-solarnom precesijom. Međutim dok se Sunce nalazi uvek u ravni ekliptike, Mesečeva staza je prema njoj nagnuta otprilike za 5°. Otuda dolazi do periodične promene Mesečevog uticaja, u vremenu od 18,66 godina[13] (to je period regresije čvorova Mesečeve staze), pa precesijska kupa nije sasvim glatka nego ispunjena naborima. Pojava nabora naziva se nutacija.[14]

Opća precesija

Veličina luni-solarne precesije iznosi 50,37" na godinu. To je ugao za koji bi se po ekliptici pomaknula proletna tačka kada bi delovali samo Mesec i Sunce. Međutim utiču još i planete. Njihov se učinak ili planetska precesija ističe kao promena položaja ravni ekliptike. Pod privlačnom silom planeta, Zemlja se njiše oko 0,05" na godinu (u današnje vreme). Zbog toga će proletna tačka kliziti i po nebeskom ekvatoru za 0,13" na godinu, pa će u smeru ekliptičkih dužina ukupan pomak iznositi 50,25" na godinu. To je godišnji iznos opšte Zemljine precesije.

Zemljina precesija dovodi do razlike između Sunčeve (tropske) i zvezdane (sideričke) godine. Zvezdana godina je vreme potrebno da Sunce na nebeskoj sferi prevali puni ugao ili, drugim rečima, vreme obilaženja Zemlje oko Sunca s obzirom na neki zadani smer u prostoru (npr. u odnosu na proletnu tačku). U Sunčevoj godini Sunce prevali nebeskom sferom ugao koji je od punog ugla manji za iznos Zemljine precesije; igao od 360° - 50,25” Sunce pređe za vreme Sunčeve godine od 365,2422 dana, a ugao od 360° za vreme zvezdane godine.[15][16] Zvezdana godina je oko 20 minuta duža od Sunčeve godine.

Platonova godina

Iz iznosa opšte precesije lako se može naći razdoblje vremena u kojem Zemljina osa obiđe precesijsku kupu, a proletna tačka puni krug po nebeskom ekvatoru. Ako pomak u jednoj godini iznosi 50,25", tada za pomak od 360° treba 25.800 godina. To je Platonova godina. U tom razdoblju nebeski pol opiše kružnicu među zvezdama. Stoga će današnju Severnjaču (α Malog medveda) zamenjivati druge zvezde. Pre 5000 godina zabeležena je kao Severnjača zvezda Tuban (α Zmaja). Oko godine 14.000. kao Severnjača će služiti zvezda Vega, iako severnom nebeskom polu neće prići bliže od 5°. Od vremena kada su astronomi imenovali sazvežđa i ustanovili Zemljinu precesiju, proletna se tačka pomaknula iz sazvežđa Ovna u sazvežđe Riba, a tako su se u susedno sazvežđe pomaknule i ostale glavne tačke ekliptike. Znakovi tih tačaka ostali su međutim isti kao što su i bili. S pomakom proletne tačke povezana je najviše i promena zvezdanih rektascenzija, dok je promena deklinacija mnogo manja.

Vidi još

Reference

  1. ^ „Gyroscope”. Oxford Dictionaries. Архивирано из оригинала 5. 5. 2015. г. Приступљено 4. 5. 2015. 
  2. ^ "Gyroscope Архивирано 2008-04-30 на сајту Wayback Machine" by Sándor Kabai, Wolfram Demonstrations Project.
  3. ^ Ivan I. Mueller, Spherical and practical astronomy as applied to geodesy (New York: Frederick Unger, 1969)
  4. ^ James G. Williams, "Contributions to the Earth's obliquity rate, precession, and nutation", Astronomical Journal 108 (1994) 711–724, pp.712&716. All equations are from Williams.
  5. ^ Vondrák, J.; Capitaine, N.; Wallace, P. (2011-10-01). „New precession expressions, valid for long time intervals”. Astronomy & Astrophysics (на језику: енглески). 534: A22. ISSN 0004-6361. doi:10.1051/0004-6361/201117274. 
  6. ^ Schaub, Hanspeter (2003), Analytical Mechanics of Space Systems, AIAA, стр. 149—150, ISBN 9781600860270, Приступљено 1. 5. 2014 
  7. ^ Astro 101 – Precession of the Equinox Архивирано на сајту Wayback Machine (2. јануар 2009), Western Washington University Planetarium, accessed 30 December 2008
  8. ^ Robert Main, Practical and Spherical Astronomy (Cambridge: 1863) pp.203–4.
  9. ^ Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) Explanatory Supplement to the Astronomical Almanac. Sausalito: University Science Books. p. 99.
  10. ^ Kaler, James B. (2002). The ever-changing sky: a guide to the celestial sphere (Reprint). Cambridge University Press. стр. 152. ISBN 978-0521499187. 
  11. ^ Precesija, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2014.
  12. ^ „IAU 2006 Resolution B1: Adoption of the P03 Precession Theory and Definition of the Ecliptic” (PDF). Архивирано из оригинала (PDF) 21. 10. 2011. г. Приступљено 24. 12. 2018. 
  13. ^ „Basics of Space Flight, Chapter 2”. Jet Propulsion Laboratory. Jet Propulsion Laboratory/NASA. 29. 10. 2013. Приступљено 26. 3. 2015. 
  14. ^ Vladis Vujnović : "Astronomija", Školska knjiga, 1989.
  15. ^ J.L. Simon et al., "Numerical expressions for precession formulae and mean elements for the Moon and the planets", Astronomy and Astrophyics 282 (1994) 663–683.
  16. ^ Dennis D. McCarthy, IERS Technical Note 13 – IERS Standards (1992) (Postscript, use PS2PDF).

Literatura

  • Мастило, Наталија (2005): Речник савремене српске географске терминологије, Географски факултет, Београд
  • Berger, A. L. (1976). „Obliquity & precession for the last 5 000 000 years”. Astronomy and Astrophysics. 51. стр. 127—135. Bibcode:1976A&A....51..127B. 
  • Capitaine, N. (2003). „Expressions for IAU 2000 precession quantities”. Astronomy and Astrophysics. 412: 567—586. Bibcode:2003A&A...412..567C. doi:10.1051/0004-6361:20031539. 
  • Dreyer, J. L. E.. A History of Astronomy from Thales to Kepler. 2nd ed. New York: Dover, 1953.
  • Evans, James. The History and Practice of Ancient Astronomy. New York: Oxford University Press, 1998.
  • Explanatory supplement to the Astronomical ephemeris and the American ephemeris and nautical almanac
  • Hilton, J.L. (2006). „Report of the International Astronomical Union Division I Working Group on Precession and the Ecliptic” (PDF). Celestial Mechanics and Dynamical Astronomy. 94. стр. 351—367. Bibcode:2006CeMDA..94..351H. doi:10.1007/s10569-006-0001-2. 
  • Lieske, J. H.; Lederle, T.; Fricke, W. (1977). „Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants”. Astron. Astrophys. 58. стр. 1—16. Bibcode:1977A&A....58....1L. 
  • Precession and the Obliquity of the Ecliptic has a comparison of values predicted by different theories
  • Pannekoek, A. A History of Astronomy. New York: Dover, 1961.
  • Parker, Richard A. "Egyptian Astronomy, Astrology, and Calendrical Reckoning." Dictionary of Scientific Biography 15:706–727.
  • Rice, Michael (1997), Egypt's Legacy: The archetypes of Western civilization, 3000–30 BC, London and New York.
  • Schütz, Michael (2000). „Hipparch und die Entdeckung der Präzession. Bemerkungen zu David Ulansey, Die Ursprünge des Mithraskultes”. Electronic Journal of Mithraic Studies. Архивирано из оригинала 04. 11. 2013. г. Приступљено 24. 12. 2018. 
  • Simon, J. L. (1994). „Numerical expressions for precession formulae and mean elements for the Moon and the planets”. Astronomy and Astrophysics. 282. стр. 663—683. Bibcode:1994A&A...282..663S. 
  • Tomkins, Peter. Secrets of the Great Pyramid. With an appendix by Livio Catullo Stecchini. New York: Harper Colophon Books, 1971.
  • Toomer, G. J. "Hipparchus." Dictionary of Scientific Biography. Vol. 15:207–224. New York: Charles Scribner's Sons, 1978.
  • Toomer, G. J. Ptolemy's Almagest. London: Duckworth, 1984.
  • Ulansey, David. The Origins of the Mithraic Mysteries: Cosmology and Salvation in the Ancient World. New York: Oxford University Press, 1989.
  • Vondrak, J.; Capitaine, N.; Wallace, P. (2011). „New precession equations, valid for long time intervals”. Astron. Astrophys. 534. стр. A22. Bibcode:2011A&A...534A..22V. doi:10.1051/0004-6361/201117274. 
  • Ward, W. R. (1982). „Comments on the long-term stability of the earth's obliquity”. Icarus. 50. стр. 444—448. Bibcode:1982Icar...50..444W. doi:10.1016/0019-1035(82)90134-8. 

Спољашње везе

source: https://sr.wikipedia.org/wiki/Precesija

    by Robert Payne

    Follow me opinions Website

    Related Posts