Clinfowiki
Sadržaj
 Za ostala značenja, vidi Nuklearna fuzija (razvrstavanje).
Za ostala značenja, vidi Nuklearna fuzija (razvrstavanje).

U fizici je nuklearna fuzija proces u kome se spaja više atomskih jezgri pri čemu nastaje teža atomska jezgra. To je praćeno oslobađanjem ili apsorpcijom energije što je ovisno o masi uključenih atomskih jezgri. Jezgre željeza i nikla imaju najveću energiju veze po nukleonu i zbog toga su one najstabilnije između svih drugih jezgri. Fuzija dvije jezgre lakših od jezgri željeza ili nikla najčešće oslobađa energiju, dok fuzija jezgri koje su teže od jezgri željeza ili nikla apsorbira energiju - obrnuto je kod reverznog procesa nuklearne fisije.
Pregled
Nuklearna fuzija lakih elemenata oslobađa energiju koja uzrokuje sjaj zvijezda i eksploziju vodikove bombe. Nuklearna fuzija težih elemenata (uz apsorpciju energije) javlja se pri ekstremnim uvjetima visoke energije ili kod eksplozije supranove. Nuklearna fuzija kod zvijezda i supranovih je glavni proces kojim se stvaraju novi prirodni elementi. Ova reakcija se koristi kod dobivanja energije fuzije.
Potrebna je znatna energija da bi se izazvala nuklearna fuzija, čak i kod najlakšeg elementa vodika. Međutim, fuzijom lakših jezgri kojom nastaje teža jezgra i slobodni neutron, obično se oslobađa više energije nego što je potrebno da bi se jezgre spojile. To je egzotermni proces kojim mogu nastati samoodržive reakcije.
Energija oslobođena u većini nuklearnih reakcija je mnogo veća od energije kemijskih reakcija, zato što je energija veze koja veže skupa nukleone u jezgri znatno veća od energije koja veže elektrone oko jezgre atoma. Na primjer, ionizacijska energija dobivena dodavanjem elektrona jezgri atoma vodika je 13,6 eV, manje od milijuntog dijela 17 MeV energije koja se oslobađa u prikazanoj reakciji D-T (deuterij-tricij).
Glavne faze ciklusa nuklearne fuzije u zvijezdama razradio je znanstvenik Hans Bethe.
Uvjeti za fuziju
Da bi došlo do fuzije potrebno je savladati znatnu energetsku barijeru. Na velikim udaljenostima dvije potpuno ionizirane atomske jezgre odbijaju jedna drugu zbog odbojnih elektrostatičkih sila koje postoje između njihovih pozitivno nabijenih protona. Kada se dvije jezgre približe na udaljenost potrebnu za pojavu fuzije elektrostatička barijera će biti savladana zbog jakih nuklearnih sila koje su na maloj udaljenosti jače od elektrostatičkih odbojnih sila.
Kada se nukleoni kao što je proton ili neutron dodaju jezgri, jaka sila privlači ih prema drugim nukleonima u tom jezgru, ali prvenstveno ih privlači prema najbližim susjednim nukleonima zbog kratkog dometa te sile. Nukleoni u nutrini jezgre imaju više susjednih nukleona nego oni nukleoni koji se nalaze na površini jezgre. Pošto manja jezgra ima veći odnos oplošja prema obujmu, energija veze po nukleonu zbog jake sile obično se povećava sa veličinom atomske jezgre, ali se približava graničnoj vrijednosti koja odgovara onoj vrijednosti koju ima potpuno okružen nukleon.
Elektrostatička sila, s druge strane, je sila koja opada s kvadratom udaljenosti, tako da na proton koji se dodaje atomskoj jezgri djeluje elektrostatičko odbijanje od svih drugih protona u jezgri. Elektrostatička energija po nukleonu povećava se zbog elektrostatičke sile, bez ograničenja s povećavanjem jezgre.
Ukupni rezultat ovih suprotnih sila je taj da se energija veze po nukleonu povećava s povećanjem veličine atomske jezgre, sve do elemenata željeza i nikla, a zatim se za teže atomske jezgre smanjuje. Na posljetku, energija veze postaje negativna i zbog toga su vrlo teške jezgre nestabilne. Četiri najčvršće vezane jezgre, padajućim redom u odnosu na energiju veze su: 62Ni, 58Fe, 56Fe, i 60Ni. Iako je izotop nikla 62Ni stabilniji, izotop željeza 56Fe je zastupljeniji. To je zbog veće brzine raspadanja 62Ni u unutrašnjosti zvijezda uzrokovanog apsorpcijom fotona.
Istaknuti izuzetak od ovog pravila je jezgra helija-4, čija je energija veze veća od energije veze litija, slijedećeg težeg elementa. Objašnjenje za takvo posebno ponašanje nam daje Paulijev princip isključivanja - kako su protoni i neutroni fermioni, oni ne mogu postojati u točno jednakom stanju. Svako stanje energije protona ili neutrona u jezgri može imati po jednu česticu gornjeg i donjeg spina. Helij-4 ima anomalno veliku energiju veze jer se njegova jezgra sastoji od dva protona i dva neutrona, tako da sva četiri nukleona mogu biti u osnovnom stanju. Bilo koji dodatni nukleoni moraju zauzimati stanje više energije.
Situacija je slična ako se približe dvije atomske jezgre. Dok se jedna jezgra približava drugoj, svi protoni jedne jezgre odbijaju sve protone u drugoj. Jaka nuklearna sila može prevladati ovo odbijanje tek kada se dvije jezgre međusobno dotaknu. Prema tome, čak i kada je krajnje energetsko stanje niže, i dalje postoji velika energetska barijera koja se mora prevladati. U kemiji je slična pojava poznata kao aktivacijska energija. U nuklearnoj fizici ona se zove Coulombova barijera.
Coulombova barijera je najmanja za izotope vodika - oni imaju samo jedan pozitivni naboj u jezgri. Jezgra u kome bi se nalazila samo dva protona ne bi bila stabilna, tako da moraju sudjelovati i neutroni, u idealnom slučaju je jedan od produkata vrlo čvrsto vezana jezgra helija.
Koristeći deuterij-tricijsko gorivo, energetska barijera je oko 0,1 MeV. U usporedbi, energija koja je potrebna za uklanjanje elektrona iz atoma vodika je 13,6 eV, što je oko 7500 puta manje. Prijelazni rezultat fuzije deuterija i tricija je nestabilna jezgra 5He, koja odmah izbacuje neutron uz energiju od 14,1 MeV. Energija uzmaka preostale jezgre 4He je 3,5 MeV, tako da je ukupno oslobođena energija 17,6 MeV. Ovo je višestruko veća energija od one koja je potrebna da bi se savladala energetska barijera.
Ukoliko energija kojom se započinje reakcija dolazi od ubrzavanja jedne jezgre, proces se zove fuzija "snop-meta" (beam-target), ukoliko su obje jezgre ubrzane to je onda fuzija "snop-snop" (beam-beam). Ukoliko su jezgre dijelovi plazme koja je blizu termalnog ekvilibrija (ravnoteže), onda se radi o termonuklearnoj fuziji. Temperatura je mjera prosječne kinetičke energije čestica, pa zagrijavanjem jezgre dobivaju energiju i mogu je dobiti dovoljno za savladavanje barijere od 0,1 MeV. Može se izračunati da je za tu vrijednost energije potrebna temperatura veća od 160 GK (gigakelvina), što je očito vrlo visoka vrijednost.
Postoje dva učinka koji smanjuju ukupnu potrebnu temperaturu. Jedan je činjenica da je temperatura prosječna kinetička energija, što znači da će pojedine jezgre na toj temperaturi stvarno imati mnogo veću energiju od 0,1 MeV, dok će ostale imati mnogo manju energiju. Upravo će jezgre koje se nalaze na visokoenergetskom repu funkcije raspodjele brzine sudjelovati u većini fuzijskih reakcija. Drugi učinak je kvantno tuneliranje. Jezgre ne moraju stvarno imati dovoljno energije da potpuno savladaju Coulombovu barijeru. Ukoliko imaju skoro dovoljno energije, one mogu proći kroz preostalu barijeru. Zbog ovih će razloga gorivo i na nižoj temperaturi sudjelovati u fuzijskim procesima, ali u manjoj mjeri.

Reakcijski presjek σ je mjera vjerojatnosti fuzijske reakcije kao funkcije relativne brzine između dvije jezgre u reakciji. Ako postoji raspodjela brzina, npr. kod termonuklearne fuzije raspodjela je termalna, tada je korisno izvesti prosjek raspodjele umnoška presjeka i brzine. Brzina reakcije (broj fuzija po obujmu u vremenu) je <σv> puta umnožak brojčane gustoće reaktanata:
Ukoliko u reakciju sudjeluje samo jedna vrsta jezgri, kao što je to kod D-D reakcija, onda se umnožak mora zamijeniti s . se povećava praktički od nule pri sobnoj temperaturi do značajnih veličina pri temperaturama od 10 do 100 keV. Na ovim temperaturama, daleko iznad tipičnih ionizacijskih energija (13,6 eV u slučaju vodika), fuzija reaktanata postoji u stanju plazme.
Ovisnost <σv> o temperaturi u uređaju s određenim vremenom zadržavanja energije izvodi se uzimajući u obzir Lawsonov kriterij.
Metode zadržavanja goriva
Fuzijska reakcija može održavati samu sebe ukoliko se dovoljna količina proizvedene energije koristi za održavanje goriva na visokoj temperaturi.
Gravitacijsko zadržavanje
Jedna od sila koja može zadržati gorivo dovoljno dobro da zadovolji Lawsonov kriterij je gravitacija. Međutim, potrebna masa je toliko velika da je gravitacijsko zadržavanje otkriveno samo kod zvijezda. Čak i uz korištenje goriva veće reaktivnosti, kao što je deuterij, bila bi potrebna masa veličine Mjeseca.
Magnetsko zadržavanje
Pošto su plazme vrlo dobri električni vodiči, magnetska polja mogu također zadržavati fuzijsko gorivo. Može se koristiti čitav niz magnetskih konfiguracija, najosnovnija razlika postoji između zrcalnog zadržavanja i toroidnog zadržavanja, posebno između Tokamaka i Stelaratora.
Inercijsko zadržavanje
Treći način zadržavanja je primjena naglog impulsa energije na veliki dio površine kuglice fuzijskog goriva, uzrokujući istovremenu imploziju i razvijanje topline do vrlo visokog tlaka i temperature. Ukoliko je gorivo dovoljne gustoće i dovoljno ugrijano, brzina fuzijske reakcije će biti dovoljno visoka za izgaranje značajnog dijela goriva prije nego što dođe do rasipanja. Da bi se postigli ovi ekstremni uvjeti, početno hladno gorivo se mora eksplozivno stlačiti. Inercijsko zadržavanje se koristi kod vodikove bombe, gdje kao pobuđivač služe x-zrake stvorene pomoću fisijske bombe. Inercijskim zadržavanjem se također pokušalo ostvariti kontroliranu nuklearnu fuziju, gdje kao pobuđivač služi laserska, ionska ili elektronska zraka, te tzv. Z-pinch.
Ispituju se i drugi principi zadržavanja, kao što su muon-katalizirana fuzija, Farnsworth-Hirschov fuzor (inercijsko elektrostatičko zadržavanje) i mjehurasta fuzija.
Načini proizvodnje fuzije
Poznato je mnoštvo načina kojima se utječe na nuklearnu fuziju. Neki su "hladni" u strogom značenju jer nijedan dio materijala (osim produkata reakcije) nije na visokoj temperaturi, neki su "hladni" u ograničenom značenju jer je većina materijala osim reaktanata na niskoj temperaturi i tlaku, a neke su "vrući" jer se njima stvaraju makroskopska područja vrlo visoke temperature i tlaka.
- Muon-katalizirana fuzija je dobro ustanovljen i ponovljiv fuzijski proces koji se dešava na uobičajenim temperaturama. Detaljno je proučavana od strane Stevena E. Jonesa tijekom ranih 1980ih godina. Nije objavljeno da je proizvedena energija veća od utrošene. Vjeruje se da proizvodnja neto energije nije moguća zbog količine energije potrebne za stvaranje muona, njihovog poluvremena raspada od 2,2 µs i zbog vjerojatnosti da se muon veže s novom alfa česticom i zbog toga prestane katalizirati fuziju.
- nuklearne reakcije niske energije su sporno područje istraživanja u cilju proizvodnje nuklearne fuzije.
Općenito hladna, a lokalno vruća fuzija:
- U sonoluminescenciji, akustički udarni valovi stvaraju privremene mjehuriće koji se urušavaju kratko nakon stvaranja, proizvodeći vrlo visoke temperature i tlakove. Tijekom 2002. godine, Rusi P. Taleyarkhan objavio je mogućnost pojavljivanja mjehuraste fuzije u privremenim mjehurićima ("sono fuzija"). Pokusi (zaključno sa 2005.) koji bi trebali utvrditi pojavu fuzije su dali proturječne rezultate. Ukoliko dolazi do fuzije to je zato što su lokalna temperatura i tlak dovoljno visoki za nastanak vruće fuzije.
- Farnsworth-Hirschov fuzor je uređaj u kome se odvija fuzija, a veličinom takav da se može postaviti na stol. Fuzija se odvija zbog visokih efektivnih temperatura koje se postižu elektrostatičkim ubrzavanjem iona. Uređaj se može jeftino napraviti, ali ne može postići pozitivan ukupni rezultat snage.
- Antimaterijom inicirana fuzija koristi malu količinu antimaterije da bi započela malu fuzijsku eksploziju. Ovo je proučavano naročito u kontekstu izrade moguće nuklearne pulsne propulzije.
To nije ni blizu praktičnog izvora energije, zbog visoke cijene proizvodnje same antimaterije.
- Piroelektrična fuzija obajvljane je u travnju 2005. godine od strane tima s UCLA. Znanstvenici su koristili [piroelektricitet|piroelektrične]] kristale zagrijane od -34 do 7 °C, kombinirane s iglama od volframa, kako bi proizveli električno polje od oko 25 gigavolti po metru za ioniziranje i ubrzavanje jezgri deuterija prema meti od erbijevog deuterida. Iako energija iona deuterija stvorenih pomoću kristala nije bila direktno izmjerena, znanstvenici su je u svom modelu procijenili na 100 keV (temperatura oko 109 K). Pri tim razinama energija dvije se jezgre deuterija mogu spojiti kako bi stvorile jezgru helija-3, neutron energije 2,45 MeV i tzv. bremsstrahlung (zakočno zračenje).
Iako je to koristan generator neutrona, uređaj nije predviđen za dobivanje energije jer troši mnogo više energije nego što je proizvodi.
Vruća fuzija:
- "Standardna" "vruća" fuzija, u kojoj gorivo dostiže ogromne temperature i tlakove unutar fuzijskog reaktora i nuklearnog oružja.
Načini u drugoj grupi su primjeri neuravnoteženih sustava, u kojima se vrlo visoke temperature i tlakovi stvaraju u relativno malim područjima koji graniče s materijalom mnogo niže temperature. Todd Rider je u svom doktoratu teorijski proučio sve neuravnotežene fuzijske sustave. On je predočio da će svi takvi sustavi gubiti energiju velikom brzinom zbog bremsstrahlunga, zračenja koja nastaje kada elektroni u plazmi udare u druge elektrone ili ione koji su na nižoj temperaturi i zbog toga iznenada usporavaju. Problem nije izrazit u vrućoj plazmi zbog toga što su raspon temperatura, a time i vrijednost usporavanja znatno manji.
Značajne fuzijske reakcije
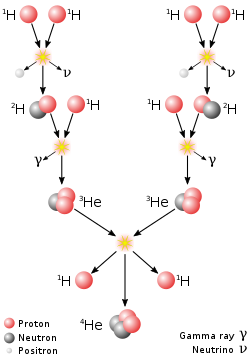
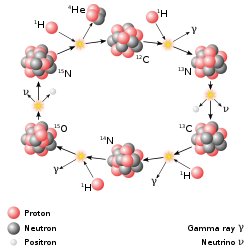
Astrofizički reakcijski nizovi
Najznačajniji fuzijski proces u prirodi je onaj koji pokreće zvijezde. Krajnji rezultat je fuzija četiri protona u jednu alfa česticu, s oslobađanjem dva pozitrona, dva neutrina i energije, međutim, ovisno o masi zvijezde, sudjeluje nekoliko pojedinačnih reakcija. Za zvijezde veličine Sunca ili manje, dominira niz proton-proton. Kod težih zvijezda, bitniji je ciklus CNO. Oba tipa procesa su odgovorna za stvaranje novih elemenata kao dio nukleosinteze zvijezda.
Na temperaturama i gustoćama u jezgrama zvijezda brzine fuzijskih reakcija su i dalje ekstremno spore. Na primjer, pri temperaturi (T ~ 15 MK) i gustoći (~120 g/cm3) u jezgri Sunca odnos stvaranje energije prema obujmu je samo ~0.1 mikrovat/cm3, što je milijun puta manje od obične svijeće i tisuću puta manje od odnosa pri stvaranja topline u ljudskom tijelu. Zbog toga je reprodukcija uvjeta iz zvjezdane jezgre u laboratoriju kako bi se dobila energija nuklearne fuzije potpuno nepraktična.
Kriteriji i kandidati za fuzijske reakcije na Zemlji
Kod fuzije koju stvara čovjek, primarno gorivo nije ograničeno na protone i mogu se koristiti više temperature, tako da se biraju reakcije s velikim presjekom. To podrazumijeva niži Lawsonov kriterij, i zbog toga manji početni napor. Drugi problem je nastanak neutrona, koji radiološki aktiviraju strukturu reaktora, ali imaju prednost zbog toga što omogućavaju volumetrijsku ekstrakciju energije fuzije i stvaranje ("oplodnju") tricija. Reakcije pri kojima se ne oslobađaju neutroni zovu se aneutronske reakcije.
Da bi bile korisne kao izvor energije, fuzijske reakcije moraju zadovoljiti nekoliko kriterija. To su:
- egzotermičnost - Ovo je možda očito, ali to ograničava reaktante na one koji se na krivulji energije vezanja nalaze na strani malih Z brojeva (broj protona). To čini helij-4 najuobičajenijim produktom zbog svog izrazito jakog vezanja nukleona u jezgri, iako se također pojavljuju i helij-3 te tricij.
- sudjelovanje jezgri s malim Z brojem - To je zbog toga što se mora prevladati elektrostatičko odbijanje prije nego što se atomske jezgre približe dovoljno blizu kako bi se spojile.
- postojanje dva reaktanta - Pri bilo kojoj gustoći koja je manja od gustoće zvijezda, sudari tri tijela su vrlo malo vjerojatni. Treba uočiti da su kod unutarnjeg zadržavanja i gustoća i temperatura mnogo veće nego kod zvijezda kako bi se kompenzirala mala vrijednost trećeg parametra Lawsonovog kriterija, vrlo kratko vrijeme zadržavanja.
- postojanje dva ili više produkata - Ovo omogućava očuvanje i energije i količine gibanja bez ovisnosti o (slaboj!) elektromagnetskoj sili.
- očuvanje i protona i neutrona - Presjeci slabe nuklearne sile su premali.
Nema puno reakcija koje zadovoljavaju sve ove zahtjeve. Prikazane su one s najvećim presjecima:
| (1) | D | + | T | → | 4He | (3,5 MeV) | + | n | (14,1 MeV) | |||||||
| (2i) | D | + | D | → | T | (1,01 MeV) | + | p | (3,02 MeV) | 50% | ||||||
| (2ii) | → | 3He | (0,82 MeV) | + | n | (2,45 MeV) | 50% | |||||||||
| (3) | D | + | 3He | → | 4He | (3,6 MeV) | + | p | (14,7 MeV) | |||||||
| (4) | T | + | T | → | 4He | + | 2 | n | + 11,3 MeV | |||||||
| (5) | 3He | + | 3He | → | 4He | + | 2 | p | + 12,9 MeV | |||||||
| (6i) | 3He | + | T | → | 4He | + | p | + | n | + 12,1 MeV | 51% | |||||
| (6ii) | → | 4He | (4,8 MeV) | + | D | (9,5 MeV) | 43% | |||||||||
| (6iii) | → | 4He | (0,5 MeV) | + | n | (1,9 MeV) | + | p | (11,9 MeV) | 6% | ||||||
| (7) | D | + | 6Li | → | 2 | 4He | + 22,4 MeV | |||||||||
| (8) | p | + | 6Li | → | 4He | (1,7 MeV) | + | 3He | (2,3 MeV) | |||||||
| (9) | 3He | + | 6Li | → | 2 | 4He | + | p | + 16,9 MeV | |||||||
| (10) | p | + | 11B | → | 3 | 4He | + 8,7 MeV |
p (procij), D (deuterij), i T (tricij) su kratice za tri glavna izotopa vodika.
Za reakcije s dva produkta, energija je između njih podijeljena u obrnutim razmjerima u odnosu na njihove mase, kao što je prikazano. U većini reakcija s tri produkta, raspodjela energije varira. Za reakcije koje mogu dati više od jednog skupa produkata dati su razmjeri grananja.
Neki kandidati za reakcije se mogu odmah eliminirati. D-6Li reakcija nema prednost u usporedbi sa p-11B jer ju je otprilike jednako teško održavati, ali proizvodi znatno više neutrona preko sporedne D-D reakcije. Tu je i p-7Li reakcija, ali je njen presjek previše mali, osim vjerojatno uz Ti > 1 MeV, ali pri tako visokim temperaturama također postaje značajna endotermička reakcija koja direktno stvara neutrone. Konačno, tu je i p-9Be reakcija, koja ne samo da se teško održava, već se 9Be može lako navesti na dijeljenje u dvije alfa čestice i neutron.
Uz fuzijske reakcije, slijedeće reakcije s neutronima su značajne zbog "oplođivanja" tricija u "suhim" fuzijskim bombama i nekim predloženim fuzijskim reaktorima:
- n + 6Li → T + 4He
- n + 7Li → T + 4He + n
Da bi se procijenila upotrebljivost ovih reakcija, u odnosu na reaktante, produkte i oslobođenu energiju, treba znati nešto i o presjeku. Za bilo koji fuzijski uređaj postoji maksimalni tlak plazme koji uređaj može izdržati, a štedljivi će uređaj uvijek raditi blizu tog maksimuma. Uz taj će se tlak najveći rezultat fuzije postići kada je temperatura izabrana tako da je <σv>/T² maksimalno. To je također i temperatura pri kojoj je vrijednost trostrukog umnoška nTT potrebnog za paljenje minimalna. Ova optimalna temperatura i vrijednost koju pri toj temperaturi ima <σv>/T² je za nekoliko takvih reakcija prikazana u slijedećoj tablici.
| gorivo | T (keV) | <σv>/T² (m³/s/keV²) |
|---|---|---|
| D-T | 13,6 | 1,24×10-24 |
| D-D | 15 | 1,28×10-26 |
| D-3He | 58 | 2,24×10-26 |
| p-6Li | 66 | 1,46×10-27 |
| p-11B | 123 | 3,01×10-27 |
Treba napomenuti da mnoge reakcije stvaraju nizove. Na primjer, reaktor koji kao gorivo koristi T i 3He stvorit će određenu količinu D, koji je onda moguće koristiti u reakciji D + 3He ukoliko su energije "ispravne". Elegantna ideja je kombinirati reakcija (8) i (9). 3He iz reakcije (8) može reagirati sa 6Li u reakciji (9) prije potpune termalizacije. Time se stvara proton visoke energije koji tada prolazi kroz reakciju (8) prije termalizacije. Detaljna analiza pokazuje da ova ideja u stvarnosti neće dobro funkcionirati, ali je dobar primjer slučaja gdje uobičajena pretpostavka plazme s Maxwell-Boltzmanovom raspodjelom nije odgovarajuća.
Neutronost, uvjeti zadržavanja i gustoća snage

Bilo koja od gore navedenih reakcija može biti osnova proizvodnje fuzijske energije. U dodatku temperaturi i presjeku o kome se već govorilo, mora se razmotriti totalna energija fuzijskih produkata. Efuz, energija električki nabijenih fuzijskih produkata Een i atomski broj Z reaktanata koji nisu vodikovi izotopi.
Specificiranje reakcije D-D ipak povlači za sobom određene teškoće. Za početak, mora se naći prosjek ogranaka (2) i (3). Teže je odlučiti kako tretirati produkte T i 3He. T u deuterijskoj plazmi tako dobro izgara da ga je iz plazme skoro nemoguće izdvojiti. Reakcija D-3He je optimalna na mnogo višim temperaturama, tako da izgaranje pri optimalnoj D-D temperaturi može biti slabo, pa izgleda razumno pretpostaviti da će T, a ne 3He, izgarati i time ukupnoj reakciji dodavati energiju. Prema tome fuzijsku energiju reakcije D-D izračunavamo kao Efuz = (4,03 + 17,6 + 3,27)/2 = 12,5 MeV, a energiju nabijenih čestica kao Een = (4,03 + 3,5 + 0,82)/2 = 4,2 MeV.
Još jedan poseban vid D-D reakcija je taj što postoji samo jedan reaktant, što se kod izračunavanja brzine reakcije mora uzeti u obzir.
S ovim izborom, u tablici su prikazani parametri za četiri najvažnije reakcije.
| gorivo | Z | Efuz (MeV) | Een (MeV) | neutronost |
|---|---|---|---|---|
| D-T | 1 | 17,6 | 3,5 | 0,80 |
| D-D | 1 | 12,5 | 4,2 | 0,66 |
| D-3He | 2 | 18,3 | 18,3 | ~0,05 |
| p-11B | 5 | 8,7 | 8,7 | ~0,001 |
Zadnji stupac pokazuje neutronost reakcije, odnosno dio fuzijske energije oslobođen u obliku neutrona. To je važan pokazatelj veličine problema povezanih s neutronima kao što su radijacijsko oštećivanje, biološki štit, daljinskog upravljanja i sigurnost. Za prve dvije reakcije izračunava se kao (Efuz - Een)/Efuz. Za zadnje dvije reakcije, gdje bi ovaj proračun dao nulu, navedene vrijednosti su grube procijene na temelju sporednih reakcija koje proizvode neutrone u plazmo koja je u termalnoj ravnoteži.
Naravno, reaktanti bi trebali biti pomiješani u optimalnim omjerima. To je slučaj kada svaki ion reaktanta i njegovi pridruženi elektroni doprinose svaki po polovicu tlaka. Pretpostavljajući da je ukupni tlak stalna vrijednost, to znači da je gustoća nevodikovih iona manja od gustoće vodikovih iona za vrijednost 2/(Z + 1). Dakle brzina tih rekcija je smanjena za istu vrijednost, pored razlike u vrijednosti za <σv>/T². S druge strane, kako D-D reakcija ima samo jedan reaktant, brzina je dva puta veća nego kada bi gorivo bilo raspodijeljeno na dvije vrste vodika.
Tako postoji "kazna" od (2/(Z + 1)) za nevodikova goriva koja proizilazi iz činjenice da im je potrebno više elektrona, koji doprinose tlaku bez učešća u reakciji fuzije. U isto vrijeme postoji i "bonus" iznosa 2 za D-D reakciju, zbog činjenice da svaki ion može reagirati sa svakim drugim ionom, a ne samo sa dijelom njih.
Sada možemo usporediti ove reakcije u slijedećoj tablici.
| gorivo | <σv>/T² | kazna/bonus | reaktivnost | Jelicev kriterijum | gustoća snage |
|---|---|---|---|---|---|
| D-T | 1,24×10-24 | 1 | 1 | 1 | 1 |
| D-D | 1,28×10-26 | 2 | 48 | 30 | 68 |
| D-3He | 2,24×10-26 | 2/3 | 83 | 16 | 80 |
| p-11B | 3,01×10-27 | 1/3 | 1240 | 500 | 2500 |
Maksimalna vrijednost <σv>/T² je uzeta iz prethodne tablice. Faktor "kazna/bonus" je povezan s nevodikovim reaktantima ili s reaktantima jedne vrste. Vrijednosti u stupcu "reaktivnost" su izračunate dijeljenjem vrijednosti 1,24×10-24 umnošcima drugog i trećeg stupca. One pokazuju faktor za koji se druge reakcije odvijaju sporije u odnosu na D-T reakcija pod usporedivim uvjetima. Stupac "Lawsonov kriterij" ponderira ove rezultate s Een i pokazuje koliko je teško postići upaljenje s tim reakcijama, relativno u odnosu na teškoću kod D-T reakcije. Zadnji stupac je označen kao "gustoća snage" i ponderira praktičnu reaktivnost s Efuz. On pokazuje koliko je puta manja fuzijska gustoća snage drugih reakcija u usporedbi s D-T reakcijom i može se smatrati mjerom ekonomskog potencijala.
Gubitci bremsstrahlunga
Ioni koji sudjeluju u fuziji u principu se nikada ne pojavljuju sami već su pomiješani s elektronima koji neutraliziraju električni naboj iona i time formiraju plazmu. Elektroni će uglavnom imati temperaturu usporedivu ili veću od temperature koju imaju ioni, pa će se sudarati s ionima i emitirati bremsstrahlung (zakočno zračenje). Sunce i zvijezde su neprozirne za bremsstahlung, ali u principu svaki fuzijski reaktor na Zemlji će pri odgovarajućim valnim dužinama biti optički tanak. Bremsstrahlung je također teško reflektirati i pretvoriti direktno u elektricitet, tako da je odnos između proizvedene fuzijske energije i gubitaka zbog bremssthalunga važna brojčana vrijednost. Ovaj odnos se uopćeno maksimizira na mnogo višim temperaturama od onih koje maksimiziraju gustoću snage (prethodni odjeljak). Tablica koja slijedi ugrubo pokazuje optimalnu temperaturu i odnos snaga na toj temperaturama za nekoliko reakcija.
| gorivo | Ti (keV) | Pfuzija/Pbremsstrahlung |
|---|---|---|
| D-T | 50 | 140 |
| D-D | 500 | 2,9 |
| D-3He | 100 | 5,3 |
| 3He-3He | 1000 | 0,72 |
| p-6Li | 800 | 0,21 |
| p-11B | 300 | 0,57 |
Stvarni odnos snaga fuzije i bremssthralunga će vjerojatno biti značajno manji zbog nekoliko razloga. Kao prvo, proračun pretpostavlja da je energija fuzijskih produkata potpuno prenijeta na ione goriva, koji onda gube energiju u sudarima s elektronima, a elektroni nadalje gube tu energiju zbog bremssthalunga. Međitim, kako se fuzijski produkti kreću znatno brže od iona goriva, oni će predati značajan dio svoje energije direktno elektronima. Drugo, za plazmu je predpostavljeno da se sastoji samo od iona goriva. U praksi, postojat će značajan udio iona nečistoća, što će smanjiti odnos. Posebno, sami fuzijski produkti moraju ostati u plazmi sve dok ne predaju svoju energiju i nakon toga će još neko vrijem biti u njoj u bilo kojoj predloženom načinu zadržavanja. Na kraju, zanemareni su svi kanali gubitka energije osim bremssthralunga. Zadnja dva čimbenika su povezana. Na temelju teorije i eksperimenata, izgleda da je zadržavanje energije i čestica blisko povezano. U načinima zadržavanja koji dobro zadržavaju energiju, doći će do porasta fuzijskih produkata. Ukoliko se fuzijski produkti efikasno izbacuju, također će biti loše i zadržavanje energije.
Temperature koje maksimiziraju snagu fuzije u odnosu na bremssthralung su u svakom slučaju višee od temperature koja maksimizira gustoću snage i minimizira potrebnu vrijednost trostrukog fuzijskog umnoška. To neće puno promijeniti optimalnu radnu točku za D-T, jer je udio bremssthralunga mali, ali će potaknuti druga goriva u stanja gdje je gustoća snage u odnosu prema D-T čak i manja, te će biti još teže postići potrebno zadržavanje. Za D-D i D-3He, bremssthralung gubitci će biti ozbiljan, vjerojatno i sprječavajući problem. Za 3He-3He, p-6Li i p-11B čini se da gubitci bremssthralunga ukazuju na nemogućnost korištenja tih goriva u fuzijskom reaktoru.


















