The US FDA’s proposed rule on laboratory-developed tests: Impacts on clinical laboratory testing
Contents
-
(Top)
-
1 Gene effects
-
2 Allele and genotype frequencies
-
2.1 Random fertilization
-
2.2 Mendel's research cross – a contrast
-
2.3 Self fertilization – an alternative
-
2.4 Population mean
-
2.5 Genetic drift
-
2.5.1 The sample gamodemes – genetic drift
-
2.5.2 The progeny lines – dispersion
-
2.5.3 The equivalent post-dispersion panmictic – inbreeding
-
2.5.4 Extensive binomial sampling – is panmixia restored?
-
2.5.5 Continued genetic drift – increased dispersion and inbreeding
-
2.5.6 Selfing within random fertilization
-
2.5.7 Homozygosity and heterozygosity
-
-
-
3 Extended principles
-
4 Relationship
-
5 Resemblances between relatives
-
6 Selection
-
8 See also
-
9 Footnotes and references
-
10 Further reading
-
11 External links
| Part of a series on |
| Genetics |
|---|
 |
Quantitative genetics is the study of quantitative traits, which are phenotypes that vary continuously—such as height or mass—as opposed to phenotypes and gene-products that are discretely identifiable—such as eye-colour, or the presence of a particular biochemical.
Both of these branches of genetics use the frequencies of different alleles of a gene in breeding populations (gamodemes), and combine them with concepts from simple Mendelian inheritance to analyze inheritance patterns across generations and descendant lines. While population genetics can focus on particular genes and their subsequent metabolic products, quantitative genetics focuses more on the outward phenotypes, and makes only summaries of the underlying genetics.
Due to the continuous distribution of phenotypic values, quantitative genetics must employ many other statistical methods (such as the effect size, the mean and the variance) to link phenotypes (attributes) to genotypes. Some phenotypes may be analyzed either as discrete categories or as continuous phenotypes, depending on the definition of cut-off points, or on the metric used to quantify them.[1]: 27–69 Mendel himself had to discuss this matter in his famous paper,[2] especially with respect to his peas' attribute tall/dwarf, which actually was derived by adding a cut-off point to "length of stem".[3][4] Analysis of quantitative trait loci, or QTLs,[5][6][7] is a more recent addition to quantitative genetics, linking it more directly to molecular genetics.
Gene effects
In diploid organisms, the average genotypic "value" (locus value) may be defined by the allele "effect" together with a dominance effect, and also by how genes interact with genes at other loci (epistasis). The founder of quantitative genetics - Sir Ronald Fisher - perceived much of this when he proposed the first mathematics of this branch of genetics.[8]

Being a statistician, he defined the gene effects as deviations from a central value—enabling the use of statistical concepts such as mean and variance, which use this idea.[9] The central value he chose for the gene was the midpoint between the two opposing homozygotes at the one locus. The deviation from there to the "greater" homozygous genotype can be named "+a"; and therefore it is "-a" from that same midpoint to the "lesser" homozygote genotype. This is the "allele" effect mentioned above. The heterozygote deviation from the same midpoint can be named "d", this being the "dominance" effect referred to above.[10] The diagram depicts the idea. However, in reality we measure phenotypes, and the figure also shows how observed phenotypes relate to the gene effects. Formal definitions of these effects recognize this phenotypic focus.[11][12] Epistasis has been approached statistically as interaction (i.e., inconsistencies),[13] but epigenetics suggests a new approach may be needed.
If 0<d<a, the dominance is regarded as partial or incomplete—while d=a indicates full or classical dominance. Previously, d>a was known as "over-dominance".[14]
Mendel's pea attribute "length of stem" provides us with a good example.[3] Mendel stated that the tall true-breeding parents ranged from 6–7 feet in stem length (183 – 213 cm), giving a median of 198 cm (= P1). The short parents ranged from 0.75 to 1.25 feet in stem length (23 – 46 cm), with a rounded median of 34 cm (= P2). Their hybrid ranged from 6–7.5 feet in length (183–229 cm), with a median of 206 cm (= F1). The mean of P1 and P2 is 116 cm, this being the phenotypic value of the homozygotes midpoint (mp). The allele affect (a) is [P1-mp] = 82 cm = -[P2-mp]. The dominance effect (d) is [F1-mp] = 90 cm.[15] This historical example illustrates clearly how phenotype values and gene effects are linked.
Allele and genotype frequencies
To obtain means, variances and other statistics, both quantities and their occurrences are required. The gene effects (above) provide the framework for quantities: and the frequencies of the contrasting alleles in the fertilization gamete-pool provide the information on occurrences.
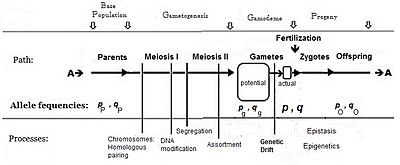
Commonly, the frequency of the allele causing "more" in the phenotype (including dominance) is given the symbol p, while the frequency of the contrasting allele is q. An initial assumption made when establishing the algebra was that the parental population was infinite and random mating, which was made simply to facilitate the derivation. The subsequent mathematical development also implied that the frequency distribution within the effective gamete-pool was uniform: there were no local perturbations where p and q varied. Looking at the diagrammatic analysis of sexual reproduction, this is the same as declaring that pP = pg = p; and similarly for q.[14] This mating system, dependent upon these assumptions, became known as "panmixia".
Panmixia rarely actually occurs in nature,[16]: 152–180 [17] as gamete distribution may be limited, for example by dispersal restrictions or by behaviour, or by chance sampling (those local perturbations mentioned above). It is well known that there is a huge wastage of gametes in Nature, which is why the diagram depicts a potential gamete-pool separately to the actual gamete-pool. Only the latter sets the definitive frequencies for the zygotes: this is the true "gamodeme" ("gamo" refers to the gametes, and "deme" derives from Greek for "population"). But, under Fisher's assumptions, the gamodeme can be effectively extended back to the potential gamete-pool, and even back to the parental base-population (the "source" population). The random sampling arising when small "actual" gamete-pools are sampled from a large "potential" gamete-pool is known as genetic drift, and is considered subsequently.
While panmixia may not be widely extant, the potential for it does occur, although it may be only ephemeral because of those local perturbations. It has been shown, for example, that the F2 derived from random fertilization of F1 individuals (an allogamous F2), following hybridization, is an origin of a new potentially panmictic population.[18][19] It has also been shown that if panmictic random fertilization occurred continually, it would maintain the same allele and genotype frequencies across each successive panmictic sexual generation—this being the Hardy Weinberg equilibrium.[13]: 34–39 [20][21][22][23] However, as soon as genetic drift was initiated by local random sampling of gametes, the equilibrium would cease.
Random fertilization
Male and female gametes within the actual fertilizing pool are considered usually to have the same frequencies for their corresponding alleles. (Exceptions have been considered.) This means that when p male gametes carrying the A allele randomly fertilize p female gametes carrying that same allele, the resulting zygote has genotype AA, and, under random fertilization, the combination occurs with a frequency of p x p (= p2). Similarly, the zygote aa occurs with a frequency of q2. Heterozygotes (Aa) can arise in two ways: when p male (A allele) randomly fertilize q female (a allele) gametes, and vice versa. The resulting frequency for the heterozygous zygotes is thus 2pq.[13]: 32 Notice that such a population is never more than half heterozygous, this maximum occurring when p=q= 0.5.
In summary then, under random fertilization, the zygote (genotype) frequencies are the quadratic expansion of the gametic (allelic) frequencies: . (The "=1" states that the frequencies are in fraction form, not percentages; and that there are no omissions within the framework proposed.)
Notice that "random fertilization" and "panmixia" are not synonyms.
Mendel's research cross – a contrast
Mendel's pea experiments were constructed by establishing true-breeding parents with "opposite" phenotypes for each attribute.[3] This meant that each opposite parent was homozygous for its respective allele only. In our example, "tall vs dwarf", the tall parent would be genotype TT with p = 1 (and q = 0); while the dwarf parent would be genotype tt with q = 1 (and p = 0). After controlled crossing, their hybrid is Tt, with p = q = 1/2. However, the frequency of this heterozygote = 1, because this is the F1 of an artificial cross: it has not arisen through random fertilization.[24] The F2 generation was produced by natural self-pollination of the F1 (with monitoring against insect contamination), resulting in p = q = 1/2 being maintained. Such an F2 is said to be "autogamous". However, the genotype frequencies (0.25 TT, 0.5 Tt, 0.25 tt) have arisen through a mating system very different from random fertilization, and therefore the use of the quadratic expansion has been avoided. The numerical values obtained were the same as those for random fertilization only because this is the special case of having originally crossed homozygous opposite parents.[25] We can notice that, because of the dominance of T- [frequency (0.25 + 0.5)] over tt [frequency 0.25], the 3:1 ratio is still obtained.
A cross such as Mendel's, where true-breeding (largely homozygous) opposite parents are crossed in a controlled way to produce an F1, is a special case of hybrid structure. The F1 is often regarded as "entirely heterozygous" for the gene under consideration. However, this is an over-simplification and does not apply generally—for example when individual parents are not homozygous, or when populations inter-hybridise to form hybrid swarms.[24] The general properties of intra-species hybrids (F1) and F2 (both "autogamous" and "allogamous") are considered in a later section.
Self fertilization – an alternative
Having noticed that the pea is naturally self-pollinated, we cannot continue to use it as an example for illustrating random fertilization properties. Self-fertilization ("selfing") is a major alternative to random fertilization, especially within Plants. Most of the Earth's cereals are naturally self-pollinated (rice, wheat, barley, for example), as well as the pulses. Considering the millions of individuals of each of these on Earth at any time, it is obvious that self-fertilization is at least as significant as random fertilization. Self-fertilization is the most intensive form of inbreeding, which arises whenever there is restricted independence in the genetical origins of gametes. Such reduction in independence arises if parents are already related, and/or from genetic drift or other spatial restrictions on gamete dispersal. Path analysis demonstrates that these are tantamount to the same thing.[26][27] Arising from this background, the inbreeding coefficient (often symbolized as F or f) quantifies the effect of inbreeding from whatever cause. There are several formal definitions of f, and some of these are considered in later sections. For the present, note that for a long-term self-fertilized species f = 1. Natural self-fertilized populations are not single " pure lines ", however, but mixtures of such lines. This becomes particularly obvious when considering more than one gene at a time. Therefore, allele frequencies (p and q) other than 1 or 0 are still relevant in these cases (refer back to the Mendel Cross section). The genotype frequencies take a different form, however.
In general, the genotype frequencies become for AA and for Aa and for aa.[13]: 65
Notice that the frequency of the heterozygote declines in proportion to f. When f = 1, these three frequencies become respectively p, 0 and q Conversely, when f = 0, they reduce to the random-fertilization quadratic expansion shown previously.
Population mean
The population mean shifts the central reference point from the homozygote midpoint (mp) to the mean of a sexually reproduced population. This is important not only to relocate the focus into the natural world, but also to use a measure of central tendency used by Statistics/Biometrics. In particular, the square of this mean is the Correction Factor, which is used to obtain the genotypic variances later.[9]

For each genotype in turn, its allele effect is multiplied by its genotype frequency; and the products are accumulated across all genotypes in the model. Some algebraic simplification usually follows to reach a succinct result.
The mean after random fertilization
The contribution of AA is , that of Aa is , and that of aa is . Gathering together the two a terms and accumulating over all, the result is: . Simplification is achieved by noting that , and by recalling that , thereby reducing the right-hand term to .
The succinct result is therefore .[14] : 110
This defines the population mean as an "offset" from the homozygote midpoint (recall a and d are defined as deviations from that midpoint). The Figure depicts G across all values of p for several values of d, including one case of slight over-dominance. Notice that G is often negative, thereby emphasizing that it is itself a deviation (from mp).
Finally, to obtain the actual Population Mean in "phenotypic space", the midpoint value is added to this offset: .
An example arises from data on ear length in maize.[28]: 103 Assuming for now that one gene only is represented, a = 5.45 cm, d = 0.12 cm [virtually "0", really], mp = 12.05 cm. Further assuming that p = 0.6 and q = 0.4 in this example population, then:
G = 5.45 (0.6 − 0.4) + (0.48)0.12 = 1.15 cm (rounded); and
P = 1.15 + 12.05 = 13.20 cm (rounded).
The mean after long-term self-fertilization
The contribution of AA is , while that of aa is . [See above for the frequencies.] Gathering these two a terms together leads to an immediately very simple final result:
. As before, .
Often, "G(f=1)" is abbreviated to "G1".
Mendel's peas can provide us with the allele effects and midpoint (see previously); and a mixed self-pollinated population with p = 0.6 and q = 0.4 provides example frequencies. Thus:
G(f=1) = 82 (0.6 − .04) = 59.6 cm (rounded); and
P(f=1) = 59.6 + 116 = 175.6 cm (rounded).
The mean – generalized fertilization
A general formula incorporates the inbreeding coefficient f, and can then accommodate any situation. The procedure is exactly the same as before, using the weighted genotype frequencies given earlier. After translation into our symbols, and further rearrangement:[13] : 77–78
Here, G0 is G, which was given earlier. (Often, when dealing with inbreeding, "G0" is preferred to "G".)
Supposing that the maize example [given earlier] had been constrained on a holme (a narrow riparian meadow), and had partial inbreeding to the extent of f = 0.25, then, using the third version (above) of Gf:
G0.25 = 1.15 − 0.25 (0.48) 0.12 = 1.136 cm (rounded), with P0.25 = 13.194 cm (rounded).
There is hardly any effect from inbreeding in this example, which arises because there was virtually no dominance in this attribute (d → 0). Examination of all three versions of Gf reveals that this would lead to trivial change in the Population mean. Where dominance was notable, however, there would be considerable change.
Genetic drift
Genetic drift was introduced when discussing the likelihood of panmixia being widely extant as a natural fertilization pattern. [See section on Allele and Genotype frequencies.] Here the sampling of gametes from the potential gamodeme is discussed in more detail. The sampling involves random fertilization between pairs of random gametes, each of which may contain either an A or an a allele. The sampling is therefore binomial sampling.[13]: 382–395 [14]: 49–63 [29]: 35 [30]: 55 Each sampling "packet" involves 2N alleles, and produces N zygotes (a "progeny" or a "line") as a result. During the course of the reproductive period, this sampling is repeated over and over, so that the final result is a mixture of sample progenies. The result is dispersed random fertilization These events, and the overall end-result, are examined here with an illustrative example.
The "base" allele frequencies of the example are those of the potential gamodeme: the frequency of A is pg = 0.75, while the frequency of a is qg = 0.25. [White label "1" in the diagram.] Five example actual gamodemes are binomially sampled out of this base (s = the number of samples = 5), and each sample is designated with an "index" k: with k = 1 .... s sequentially. (These are the sampling "packets" referred to in the previous paragraph.) The number of gametes involved in fertilization varies from sample to sample, and is given as 2Nk [at white label "2" in the diagram]. The total (Σ) number of gametes sampled overall is 52 [white label "3" in the diagram]. Because each sample has its own size, weights are needed to obtain averages (and other statistics) when obtaining the overall results. These are , and are given at white label "4" in the diagram.

The sample gamodemes – genetic drift
Following completion of these five binomial sampling events, the resultant actual gamodemes each contained different allele frequencies—(pk and qk). [These are given at white label "5" in the diagram.] This outcome is actually the genetic drift itself. Notice that two samples (k = 1 and 5) happen to have the same frequencies as the base (potential) gamodeme. Another (k = 3) happens to have the p and q "reversed". Sample (k = 2) happens to be an "extreme" case, with pk = 0.9 and qk = 0.1; while the remaining sample (k = 4) is "middle of the range" in its allele frequencies. All of these results have arisen only by "chance", through binomial sampling. Having occurred, however, they set in place all the downstream properties of the progenies.
Because sampling involves chance, the probabilities ( ∫k ) of obtaining each of these samples become of interest. These binomial probabilities depend on the starting frequencies (pg and qg) and the sample size (2Nk). They are tedious to obtain,[13]: 382–395 [30]: 55 but are of considerable interest. [See white label "6" in the diagram.] The two samples (k = 1, 5), with the allele frequencies the same as in the potential gamodeme, had higher "chances" of occurring than the other samples. Their binomial probabilities did differ, however, because of their different sample sizes (2Nk). The "reversal" sample (k = 3) had a very low Probability of occurring, confirming perhaps what might be expected. The "extreme" allele frequency gamodeme (k = 2) was not "rare", however; and the "middle of the range" sample (k=4) was rare. These same Probabilities apply also to the progeny of these fertilizations.
Here, some summarizing can begin. The overall allele frequencies in the progenies bulk are supplied by weighted averages of the appropriate frequencies of the individual samples. That is: and . (Notice that k is replaced by • for the overall result—a common practice.)[9] The results for the example are p• = 0.631 and q• = 0.369 [black label "5" in the diagram]. These values are quite different to the starting ones (pg and qg) [white label "1"]. The sample allele frequencies also have variance as well as an average. This has been obtained using the sum of squares (SS) method [31] [See to the right of black label "5" in the diagram]. [Further discussion on this variance occurs in the section below on Extensive genetic drift.]
The progeny lines – dispersion
The genotype frequencies of the five sample progenies are obtained from the usual quadratic expansion of their respective allele frequencies (random fertilization). The results are given at the diagram's white label "7" for the homozygotes, and at white label "8" for the heterozygotes. Re-arrangement in this manner prepares the way for monitoring inbreeding levels. This can be done either by examining the level of total homozygosis [(p2k + q2k) = (1 − 2pkqk)], or by examining the level of heterozygosis (2pkqk), as they are complementary.[32] Notice that samples k= 1, 3, 5 all had the same level of heterozygosis, despite one being the "mirror image" of the others with respect to allele frequencies. The "extreme" allele-frequency case (k= 2) had the most homozygosis (least heterozygosis) of any sample. The "middle of the range" case (k= 4) had the least homozygosity (most heterozygosity): they were each equal at 0.50, in fact.
The overall summary can continue by obtaining the weighted average of the respective genotype frequencies for the progeny bulk. Thus, for AA, it is , for Aa, it is and for aa, it is . The example results are given at black label "7" for the homozygotes, and at black label "8" for the heterozygote. Note that the heterozygosity mean is 0.3588, which the next section uses to examine inbreeding resulting from this genetic drift.
The next focus of interest is the dispersion itself, which refers to the "spreading apart" of the progenies' population means. These are obtained as [see section on the Population mean], for each sample progeny in turn, using the example gene effects given at white label "9" in the diagram. Then, each is obtained also [at white label "10" in the diagram]. Notice that the "best" line (k = 2) had the highest allele frequency for the "more" allele (A) (it also had the highest level of homozygosity). The worst progeny (k = 3) had the highest frequency for the "less" allele (a), which accounted for its poor performance. This "poor" line was less homozygous than the "best" line; and it shared the same level of homozygosity, in fact, as the two second-best lines (k = 1, 5). The progeny line with both the "more" and the "less" alleles present in equal frequency (k = 4) had a mean below the overall average (see next paragraph), and had the lowest level of homozygosity. These results reveal the fact that the alleles most prevalent in the "gene-pool" (also called the "germplasm") determine performance, not the level of homozygosity per se. Binomial sampling alone effects this dispersion.
The overall summary can now be concluded by obtaining and . The example result for P• is 36.94 (black label "10" in the diagram). This later is used to quantify inbreeding depression overall, from the gamete sampling. [See the next section.] However, recall that some "non-depressed" progeny means have been identified already (k = 1, 2, 5). This is an enigma of inbreeding—while there may be "depression" overall, there are usually superior lines among the gamodeme samplings.
The equivalent post-dispersion panmictic – inbreeding
Included in the overall summary were the average allele frequencies in the mixture of progeny lines (p• and q•). These can now be used to construct a hypothetical panmictic equivalent.[13]: 382–395 [14]: 49–63 [29]: 35 This can be regarded as a "reference" to assess the changes wrought by the gamete sampling. The example appends such a panmictic to the right of the Diagram. The frequency of AA is therefore (p•)2 = 0.3979. This is less than that found in the dispersed bulk (0.4513 at black label "7"). Similarly, for aa, (q•)2 = 0.1303—again less than the equivalent in the progenies bulk (0.1898). Clearly, genetic drift has increased the overall level of homozygosis by the amount (0.6411 − 0.5342) = 0.1069. In a complementary approach, the heterozygosity could be used instead. The panmictic equivalent for Aa is 2 p• q• = 0.4658, which is higher than that in the sampled bulk (0.3588) [black label "8"]. The sampling has caused the heterozygosity to decrease by 0.1070, which differs trivially from the earlier estimate because of rounding errors.
The inbreeding coefficient (f) was introduced in the early section on Self Fertilization. Here, a formal definition of it is considered: f is the probability that two "same" alleles (that is A and A, or a and a), which fertilize together are of common ancestral origin—or (more formally) f is the probability that two homologous alleles are autozygous.[14][27] Consider any random gamete in the potential gamodeme that has its syngamy partner restricted by binomial sampling. The probability that that second gamete is homologous autozygous to the first is 1/(2N), the reciprocal of the gamodeme size. For the five example progenies, these quantities are 0.1, 0.0833, 0.1, 0.0833 and 0.125 respectively, and their weighted average is 0.0961. This is the inbreeding coefficient of the example progenies bulk, provided it is unbiased with respect to the full binomial distribution. An example based upon s = 5 is likely to be biased, however, when compared to an appropriate entire binomial distribution based upon the sample number (s) approaching infinity (s → ∞). Another derived definition of f for the full Distribution is that f also equals the rise in homozygosity, which equals the fall in heterozygosity.[33] For the example, these frequency changes are 0.1069 and 0.1070, respectively. This result is different to the above, indicating that bias with respect to the full underlying distribution is present in the example. For the example itself, these latter values are the better ones to use, namely f• = 0.10695.
The population mean of the equivalent panmictic is found as [a (p•-q•) + 2 p•q• d] + mp. Using the example gene effects (white label "9" in the diagram), this mean is 37.87. The equivalent mean in the dispersed bulk is 36.94 (black label "10"), which is depressed by the amount 0.93. This is the inbreeding depression from this Genetic Drift. However, as noted previously, three progenies were not depressed (k = 1, 2, 5), and had means even greater than that of the panmictic equivalent. These are the lines a plant breeder looks for in a line selection programme.[34]
Extensive binomial sampling – is panmixia restored?
If the number of binomial samples is large (s → ∞ ), then p• → pg and q• → qg. It might be queried whether panmixia would effectively re-appear under these circumstances. However, the sampling of allele frequencies has still occurred, with the result that σ2p, q ≠ 0.[35] In fact, as s → ∞, the , which is the variance of the whole binomial distribution.[13]: 382–395 [14]: 49–63 Furthermore, the "Wahlund equations" show that the progeny-bulk homozygote frequencies can be obtained as the sums of their respective average values (p2• or q2•) plus σ2p, q.[13]: 382–395 Likewise, the bulk heterozygote frequency is (2 p• q•) minus twice the σ2p, q. The variance arising from the binomial sampling is conspicuously present. Thus, even when s → ∞, the progeny-bulk genotype frequencies still reveal increased homozygosis, and decreased heterozygosis, there is still dispersion of progeny means, and still inbreeding and inbreeding depression. That is, panmixia is not re-attained once lost because of genetic drift (binomial sampling). However, a new potential panmixia can be initiated via an allogamous F2 following hybridization.[36]
Continued genetic drift – increased dispersion and inbreeding
Previous discussion on genetic drift examined just one cycle (generation) of the process. When the sampling continues over successive generations, conspicuous changes occur in σ2p, q and f. Furthermore, another "index" is needed to keep track of "time": t = 1 .... y where y = the number of "years" (generations) considered. The methodology often is to add the current binomial increment (Δ = "de novo") to what has occurred previously.[13] The entire Binomial Distribution is examined here. [There is no further benefit to be had from an abbreviated example.]
Dispersion via σ2p,q
Earlier this variance (σ 2p,q[35]) was seen to be:-
With the extension over time, this is also the result of the first cycle, and so is (for brevity). At cycle 2, this variance is generated yet again—this time becoming the de novo variance ()—and accumulates to what was present already—the "carry-over" variance. The second cycle variance () is the weighted sum of these two components, the weights being for the de novo and = for the"carry-over".
Thus,
| 1 |
The extension to generalize to any time t, after considerable simplification, becomes:[13]: 328 -
| 2 |
Because it was this variation in allele frequencies that caused the "spreading apart" of the progenies' means (dispersion), the change in σ2t over the generations indicates the change in the level of the dispersion.
Dispersion via f
The method for examining the inbreeding coefficient is similar to that used for σ 2p,q. The same weights as before are used respectively for de novo f ( Δ f ) [recall this is 1/(2N) ] and carry-over f. Therefore, , which is similar to Equation (1) in the previous sub-section.

In general, after rearrangement,[13] The graphs to the left show levels of inbreeding over twenty generations arising from genetic drift for various actual gamodeme sizes (2N).
Still further rearrangements of this general equation reveal some interesting relationships.
(A) After some simplification,[13] . The left-hand side is the difference between the current and previous levels of inbreeding: the change in inbreeding (δft). Notice, that this change in inbreeding (δft) is equal to the de novo inbreeding (Δf) only for the first cycle—when ft-1 is zero.
(B) An item of note is the (1-ft-1), which is an "index of non-inbreeding". It is known as the panmictic index.[13][14] .
(C) Further useful relationships emerge involving the panmictic index.[13][14] . (D) A key link emerges between σ 2p,q and f. Firstly...[13] Secondly, presuming that f0 = 0, the right-hand side of this equation reduces to the section within the brackets of Equation (2) at the end of the last sub-section. That is, if initially there is no inbreeding, ! Furthermore, if this then is rearranged, . That is, when initial inbreeding is zero, the two principal viewpoints of binomial gamete sampling (genetic drift) are directly inter-convertible.
Selfing within random fertilization

It is easy to overlook that random fertilization includes self-fertilization. Sewall Wright showed that a proportion 1/N of random fertilizations is actually self fertilization , with the remainder (N-1)/N being cross fertilization . Following path analysis and simplification, the new view random fertilization inbreeding was found to be: .[27][37] Upon further rearrangement, the earlier results from the binomial sampling were confirmed, along with some new arrangements. Two of these were potentially very useful, namely: (A) ; and (B) .
The recognition that selfing may intrinsically be a part of random fertilization leads to some issues about the use of the previous random fertilization 'inbreeding coefficient'. Clearly, then, it is inappropriate for any species incapable of self fertilization, which includes plants with self-incompatibility mechanisms, dioecious plants, and bisexual animals. The equation of Wright was modified later to provide a version of random fertilization that involved only cross fertilization with no self fertilization. The proportion 1/N formerly due to selfing now defined the carry-over gene-drift inbreeding arising from the previous cycle. The new version is:[13]: 166 .
The graphs to the right depict the differences between standard random fertilization RF, and random fertilization adjusted for "cross fertilization alone" CF. As can be seen, the issue is non-trivial for small gamodeme sample sizes.
It now is necessary to note that not only is "panmixia" not a synonym for "random fertilization", but also that "random fertilization" is not a synonym for "cross fertilization".
Homozygosity and heterozygosity
In the sub-section on "The sample gamodemes – Genetic drift", a series of gamete samplings was followed, an outcome of which was an increase in homozygosity at the expense of heterozygosity. From this viewpoint, the rise in homozygosity was due to the gamete samplings. Levels of homozygosity can be viewed also according to whether homozygotes arose allozygously or autozygously. Recall that autozygous alleles have the same allelic origin, the likelihood (frequency) of which is the inbreeding coefficient (f) by definition. The proportion arising allozygously is therefore (1-f). For the A-bearing gametes, which are present with a general frequency of p, the overall frequency of those that are autozygous is therefore (f p). Similarly, for a-bearing gametes, the autozygous frequency is (f q).[38] These two viewpoints regarding genotype frequencies must be connected to establish consistency.
Following firstly the auto/allo viewpoint, consider the allozygous component. This occurs with the frequency of (1-f), and the alleles unite according to the random fertilization quadratic expansion. Thus: Consider next the autozygous component. As these alleles are autozygous, they are effectively selfings, and produce either AA or aa genotypes, but no heterozygotes. They therefore produce "AA" homozygotes plus "aa" homozygotes. Adding these two components together results in: for the AA homozygote; for the aa homozygote; and for the Aa heterozygote.[13]: 65 [14] This is the same equation as that presented earlier in the section on "Self fertilization – an alternative". The reason for the decline in heterozygosity is made clear here. Heterozygotes can arise only from the allozygous component, and its frequency in the sample bulk is just (1-f): hence this must also be the factor controlling the frequency of the heterozygotes.
Secondly, the sampling viewpoint is re-examined. Previously, it was noted that the decline in heterozygotes was . This decline is distributed equally towards each homozygote; and is added to their basic random fertilization expectations. Therefore, the genotype frequencies are: for the "AA" homozygote; for the "aa" homozygote; and for the heterozygote.
Thirdly, the consistency between the two previous viewpoints needs establishing. It is apparent at once [from the corresponding equations above] that the heterozygote frequency is the same in both viewpoints. However, such a straightforward result is not immediately apparent for the homozygotes. Begin by considering the AA homozygote's final equation in the auto/allo paragraph above:- . Expand the brackets, and follow by re-gathering [within the resultant] the two new terms with the common-factor f in them. The result is: . Next, for the parenthesized " p20 ", a (1-q) is substituted for a p, the result becoming . Following that substitution, it is a straightforward matter of multiplying-out, simplifying and watching signs. The end result is , which is exactly the result for AA in the sampling paragraph. The two viewpoints are therefore consistent for the AA homozygote. In a like manner, the consistency of the aa viewpoints can also be shown. The two viewpoints are consistent for all classes of genotypes.
Extended principles
Other fertilization patterns
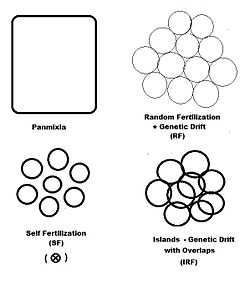
In previous sections, dispersive random fertilization (genetic drift) has been considered comprehensively, and self-fertilization and hybridizing have been examined to varying degrees. The diagram to the left depicts the first two of these, along with another "spatially based" pattern: islands. This is a pattern of random fertilization featuring dispersed gamodemes, with the addition of "overlaps" in which non-dispersive random fertilization occurs. With the islands pattern, individual gamodeme sizes (2N) are observable, and overlaps (m) are minimal. This is one of Sewall Wright's array of possibilities.[37] In addition to "spatially" based patterns of fertilization, there are others based on either "phenotypic" or "relationship" criteria. The phenotypic bases include assortative fertilization (between similar phenotypes) and disassortative fertilization (between opposite phenotypes). The relationship patterns include sib crossing, cousin crossing and backcrossing—and are considered in a separate section. Self fertilization may be considered both from a spatial or relationship point of view.
"Islands" random fertilization
The breeding population consists of s small dispersed random fertilization gamodemes of sample size ( k = 1 ... s ) with " overlaps " of proportion in which non-dispersive random fertilization occurs. The dispersive proportion is thus . The bulk population consists of weighted averages of sample sizes, allele and genotype frequencies and progeny means, as was done for genetic drift in an earlier section. However, each gamete sample size is reduced to allow for the overlaps, thus finding a effective for .

For brevity, the argument is followed further with the subscripts omitted. Recall that is in general. [Here, and following, the 2N refers to the previously defined sample size, not to any "islands adjusted" version.]
After simplification,[37] Notice that when m = 0 this reduces to the previous Δ f. The reciprocal of this furnishes an estimate of the " effective for ", mentioned above.
This Δf is also substituted into the previous inbreeding coefficient to obtain [37] where t is the index over generations, as before.
The effective overlap proportion can be obtained also,[37] as
The graphs to the right show the inbreeding for a gamodeme size of 2N = 50 for ordinary dispersed random fertilization (RF) (m=0), and for four overlap levels ( m = 0.0625, 0.125, 0.25, 0.5 ) of islands random fertilization. There has indeed been reduction in the inbreeding resulting from the non-dispersed random fertilization in the overlaps. It is particularly notable as m → 0.50. Sewall Wright suggested that this value should be the limit for the use of this approach.[37]
Allele shuffling – allele substitution
The gene-model examines the heredity pathway from the point of view of "inputs" (alleles/gametes) and "outputs" (genotypes/zygotes), with fertilization being the "process" converting one to the other. An alternative viewpoint concentrates on the "process" itself, and considers the zygote genotypes as arising from allele shuffling. In particular, it regards the results as if one allele had "substituted" for the other during the shuffle, together with a residual that deviates from this view. This formed an integral part of Fisher's method,[8] in addition to his use of frequencies and effects to generate his genetical statistics.[14] A discursive derivation of the allele substitution alternative follows.[14]: 113

Suppose that the usual random fertilization of gametes in a "base" gamodeme—consisting of p gametes (A) and q gametes (a)—is replaced by fertilization with a "flood" of gametes all containing a single allele (A or a, but not both). The zygotic results can be interpreted in terms of the "flood" allele having "substituted for" the alternative allele in the underlying "base" gamodeme. The diagram assists in following this viewpoint: the upper part pictures an A substitution, while the lower part shows an a substitution. (The diagram's "RF allele" is the allele in the "base" gamodeme.)
Consider the upper part firstly. Because base A is present with a frequency of p, the substitute A fertilizes it with a frequency of p resulting in a zygote AA with an allele effect of a. Its contribution to the outcome, therefore, is the product . Similarly, when the substitute fertilizes base a (resulting in Aa with a frequency of q and heterozygote effect of d), the contribution is . The overall result of substitution by A is, therefore, . This is now oriented towards the population mean [see earlier section] by expressing it as a deviate from that mean :
After some algebraic simplification, this becomes - the substitution effect of A.
A parallel reasoning can be applied to the lower part of the diagram, taking care with the differences in frequencies and gene effects. The result is the substitution effect of a, which is The common factor inside the brackets is the average allele substitution effect,[14]: 113 and is It can also be derived in a more direct way, but the result is the same.[39]
In subsequent sections, these substitution effects help define the gene-model genotypes as consisting of a partition predicted by these new effects (substitution expectations), and a residual (substitution deviations) between these expectations and the previous gene-model effects. The expectations are also called the breeding values and the deviations are also called dominance deviations.
Ultimately, the variance arising from the substitution expectations becomes the so-called Additive genetic variance (σ2A)[14] (also the Genic variance [40])— while that arising from the substitution deviations becomes the so-called Dominance variance (σ2D). It is noticeable that neither of these terms reflects the true meanings of these variances. The "genic variance" is less dubious than the additive genetic variance, and more in line with Fisher's own name for this partition.[8][29]: 33 A less-misleading name for the dominance deviations variance is the "quasi-dominance variance" [see following sections for further discussion]. These latter terms are preferred herein.
Gene effects redefined
The gene-model effects (a, d and -a) are important soon in the derivation of the deviations from substitution, which were first discussed in the previous Allele Substitution section. However, they need to be redefined themselves before they become useful in that exercise. They firstly need to be re-centralized around the population mean (G), and secondly they need to be re-arranged as functions of β, the average allele substitution effect.
Consider firstly the re-centralization. The re-centralized effect for AA is a• = a - G which, after simplification, becomes a• = 2q(a-pd). The similar effect for Aa is d• = d - G = a(q-p) + d(1-2pq), after simplification. Finally, the re-centralized effect for aa is (-a)• = -2p(a+qd).[14]: 116–119
Secondly, consider the re-arrangement of these re-centralized effects as functions of β. Recalling from the "Allele Substitution" section that β = [a +(q-p)d], rearrangement gives a = [β -(q-p)d]. After substituting this for a in a• and simplifying, the final version becomes a•• = 2q(β-qd). Similarly, d• becomes d•• = β(q-p) + 2pqd; and (-a)• becomes (-a)•• = -2p(β+pd).[14]: 118
Genotype substitution – expectations and deviations
The zygote genotypes are the target of all this preparation. The homozygous genotype AA is a union of two substitution effects of A, one from each sex. Its substitution expectation is therefore βAA = 2βA = 2qβ (see previous sections). Similarly, the substitution expectation of Aa is βAa = βA + βa = (q-p)β; and for aa, βaa = 2βa = -2pβ. These substitution expectations of the genotypes are also called breeding values.[14]: 114–116
Substitution deviations are the differences between these expectations and the gene effects after their two-stage redefinition in the previous section. Therefore, dAA = a•• - βAA = -2q2d after simplification. Similarly, dAa = d•• - βAa = 2pqd after simplification. Finally, daa = (-a)•• - βaa = -2p2d after simplification.[14]: 116–119 Notice that all of these substitution deviations ultimately are functions of the gene-effect d—which accounts for the use of ["d" plus subscript] as their symbols. However, it is a serious non sequitur in logic to regard them as accounting for the dominance (heterozygosis) in the entire gene model : they are simply functions of "d" and not an audit of the "d" in the system. They are as derived: deviations from the substitution expectations!
The "substitution expectations" ultimately give rise to the σ2A (the so-called "Additive" genetic variance); and the "substitution deviations" give rise to the σ2D (the so-called "Dominance" genetic variance). Be aware, however, that the average substitution effect (β) also contains "d" [see previous sections], indicating that dominance is also embedded within the "Additive" variance [see following sections on the Genotypic Variance for their derivations]. Remember also [see previous paragraph] that the "substitution deviations" do not account for the dominance in the system (being nothing more than deviations from the substitution expectations), but which happen to consist algebraically of functions of "d". More appropriate names for these respective variances might be σ2B (the "Breeding expectations" variance) and σ2δ (the "Breeding deviations" variance). However, as noted previously, "Genic" (σ 2A) and "Quasi-Dominance" (σ 2D), respectively, will be preferred herein.
Genotypic variance
There are two major approaches to defining and partitioning genotypic variance. One is based on the gene-model effects,[40] while the other is based on the genotype substitution effects[14] They are algebraically inter-convertible with each other.[36] In this section, the basic random fertilization derivation is considered, with the effects of inbreeding and dispersion set aside. This is dealt with later to arrive at a more general solution. Until this mono-genic treatment is replaced by a multi-genic one, and until epistasis is resolved in the light of the findings of epigenetics, the Genotypic variance has only the components considered here.
Gene-model approach – Mather Jinks Hayman

It is convenient to follow the biometrical approach, which is based on correcting the unadjusted sum of squares (USS) by subtracting the correction factor (CF). Because all effects have been examined through frequencies, the USS can be obtained as the sum of the products of each genotype's frequency' and the square of its gene-effect. The CF in this case is the mean squared. The result is the SS, which, again because of the use of frequencies, is also immediately the variance.[9]
The , and the . The
After partial simplification, The last line is in Mather's terminology.[40]: 212 [41][42]
Here, σ2a is the homozygote or allelic variance, and σ2d is the heterozygote or dominance variance. The substitution deviations variance (σ2D) is also present. The (weighted_covariance)ad[43] is abbreviated hereafter to " covad ".
These components are plotted across all values of p in the accompanying figure. Notice that covad is negative for p > 0.5.
Most of these components are affected by the change of central focus from homozygote mid-point (mp) to population mean (G), the latter being the basis of the Correction Factor. The covad and substitution deviation variances are simply artifacts of this shift. The allelic and dominance variances are genuine genetical partitions of the original gene-model, and are the only eu-genetical components. Even then, the algebraic formula for the allelic variance is effected by the presence of G: it is only the dominance variance (i.e. σ2d ) which is unaffected by the shift from mp to G.[36] These insights are commonly not appreciated.
Further gathering of terms [in Mather format] leads to , where . It is useful later in Diallel analysis, which is an experimental design for estimating these genetical statistics.[44]
If, following the last-given rearrangements, the first three terms are amalgamated together, rearranged further and simplified, the result is the variance of the Fisherian substitution expectation.
That is:
Notice particularly that σ2A is not σ2a. The first is the substitution expectations variance, while the second is the allelic variance.[45] Notice also that σ2D (the substitution-deviations variance) is not σ2d (the dominance variance), and recall that it is an artifact arising from the use of G for the Correction Factor. [See the "blue paragraph" above.] It now will be referred to as the "quasi-dominance" variance.
Also note that σ2D < σ2d ("2pq" being always a fraction); and note that (1) σ2D = 2pq σ2d, and that (2) σ2d = σ2D / (2pq). That is: it is confirmed that σ2D does not quantify the dominance variance in the model. It is σ2d which does that. However, the dominance variance (σ2d) can be estimated readily from the σ2D if 2pq is available.
From the Figure, these results can be visualized as accumulating σ2a, σ2d and covad to obtain σ2A, while leaving the σ2D still separated. It is clear also in the Figure that σ2D < σ2d, as expected from the equations.
The overall result (in Fisher's format) is The Fisherian components have just been derived, but their derivation via the substitution effects themselves is given also, in the next section.
Allele-substitution approach – Fisher

Reference to the several earlier sections on allele substitution reveals that the two ultimate effects are genotype substitution expectations and genotype substitution deviations. Notice that these are each already defined as deviations from the random fertilization population mean (G). For each genotype in turn therefore, the product of the frequency and the square of the relevant effect is obtained, and these are accumulated to obtain directly a SS and σ2.[46] Details follow.
σ2A = p2 βAA2 + 2pq βAa2 + q2 βaa2, which simplifies to σ2A = 2pqβ2—the Genic variance.
σ2D = p2 dAA2 + 2pq dAa2 + q daa2, which simplifies to σ2D = (2pq)2 d2—the quasi-Dominance variance.
Upon accumulating these results, σ2G = σ2A + σ2D . These components are visualized in the graphs to the right. The average allele substitution effect is graphed also, but the symbol is "α" (as is common in the citations) rather than "β" (as is used herein).
Once again, however, refer to the earlier discussions about the true meanings and identities of these components. Fisher himself did not use these modern terms for his components. The substitution expectations variance he named the "genetic" variance; and the substitution deviations variance he regarded simply as the unnamed residual between the "genotypic" variance (his name for it) and his "genetic" variance.[8][29]: 33 [47][48] [The terminology and derivation used in this article are completely in accord with Fisher's own.] Mather's term for the expectations variance—"genic"[40]—is obviously derived from Fisher's term, and avoids using "genetic" (which has become too generalized in usage to be of value in the present context). The origin is obscure of the modern misleading terms "additive" and "dominance" variances.
Note that this allele-substitution approach defined the components separately, and then totaled them to obtain the final Genotypic variance. Conversely, the gene-model approach derived the whole situation (components and total) as one exercise. Bonuses arising from this were (a) the revelations about the real structure of σ2A, and (b) the real meanings and relative sizes of σ2d and σ2D (see previous sub-section). It is also apparent that a "Mather" analysis is more informative, and that a "Fisher" analysis can always be constructed from it. The opposite conversion is not possible, however, because information about covad would be missing.
Dispersion and the genotypic variance
In the section on genetic drift, and in other sections that discuss inbreeding, a major outcome from allele frequency sampling has been the dispersion of progeny means. This collection of means has its own average, and also has a variance: the amongst-line variance. (This is a variance of the attribute itself, not of allele frequencies.) As dispersion develops further over succeeding generations, this amongst-line variance would be expected to increase. Conversely, as homozygosity rises, the within-lines variance would be expected to decrease. The question arises therefore as to whether the total variance is changing—and, if so, in what direction. To date, these issues have been presented in terms of the genic (σ 2A ) and quasi-dominance (σ 2D ) variances rather than the gene-model components. This will be done herein as well.
The crucial overview equation comes from Sewall Wright,[13] : 99, 130 [37] and is the outline of the inbred genotypic variance based on a weighted average of its extremes, the weights being quadratic with respect to the inbreeding coefficient . This equation is:
where is the inbreeding coefficient, is the genotypic variance at f=0, is the genotypic variance at f=1, is the population mean at f=0, and is the population mean at f=1.
The component [in the equation above] outlines the reduction of variance within progeny lines. The component addresses the increase in variance amongst progeny lines. Lastly, the component is seen (in the next line) to address the quasi-dominance variance.[13] : 99 & 130 These components can be expanded further thereby revealing additional insight. Thus:-
Firstly, σ2G(0) [in the equation above] has been expanded to show its two sub-components [see section on "Genotypic variance"]. Next, the σ2G(1) has been converted to 4pqa2 , and is derived in a section following. The third component's substitution is the difference between the two "inbreeding extremes" of the population mean [see section on the "Population Mean"].[36]

Summarising: the within-line components are and ; and the amongst-line components are and .[36]

Rearranging gives the following: The version in the last line is discussed further in a subsequent section.
Similarly,
Graphs to the left show these three genic variances, together with the three quasi-dominance variances, across all values of f, for p = 0.5 (at which the quasi-dominance variance is at a maximum). Graphs to the right show the Genotypic variance partitions (being the sums of the respective genic and quasi-dominance partitions) changing over ten generations with an example f = 0.10.
Answering, firstly, the questions posed at the beginning about the total variances [the Σ in the graphs] : the genic variance rises linearly with the inbreeding coefficient, maximizing at twice its starting level. The quasi-dominance variance declines at the rate of (1 − f2 ) until it finishes at zero. At low levels of f, the decline is very gradual, but it accelerates with higher levels of f.
Secondly, notice the other trends. It is probably intuitive that the within line variances decline to zero with continued inbreeding, and this is seen to be the case (both at the same linear rate (1-f) ). The amongst line variances both increase with inbreeding up to f = 0.5, the genic variance at the rate of 2f, and the quasi-dominance variance at the rate of (f − f2). At f > 0.5, however, the trends change. The amongst line genic variance continues its linear increase until it equals the total genic variance. But, the amongst line quasi-dominance variance now declines towards zero, because (f − f2) also declines with f > 0.5.[36]
Derivation of σ2G(1)
Recall that when f=1, heterozygosity is zero, within-line variance is zero, and all genotypic variance is thus amongst-line variance and deplete of dominance variance. In other words, σ2G(1) is the variance amongst fully inbred line means. Recall further [from "The mean after self-fertilization" section] that such means (G1's, in fact) are G = a(p-q). Substituting (1-q) for the p, gives G1 = a (1 − 2q) = a − 2aq.[14]: 265 Therefore, the σ2G(1) is the σ2(a-2aq) actually. Now, in general, the variance of a difference (x-y) is [ σ2x + σ2y − 2 covxy ].[49]: 100 [50] : 232 Therefore, σ2G(1) = [ σ2a + σ22aq − 2 cov(a, 2aq) ] . But a (an allele effect) and q (an allele frequency) are independent—so this covariance is zero. Furthermore, a is a constant from one line to the next, so σ2a is also zero. Further, 2a is another constant (k), so the σ22aq is of the type σ2k X. In general, the variance σ2k X is equal to k2 σ2X .[50]: 232 Putting all this together reveals that σ2(a-2aq) = (2a)2 σ2q . Recall [from the section on "Continued genetic drift"] that σ2q = pq f . With f=1 here within this present derivation, this becomes pq 1 (that is pq), and this is substituted into the previous.
The final result is: σ2G(1) = σ2(a-2aq) = 4a2 pq = 2(2pq a2) = 2 σ2a .
It follows immediately that f σ2G(1) = f 2 σ2a . [This last f comes from the initial Sewall Wright equation : it is not the f just set to "1" in the derivation concluded two lines above.]
Total dispersed genic variance – σ2A(f) and βf
Previous sections found that the within line genic variance is based upon the substitution-derived genic variance ( σ2A )—but the amongst line genic variance is based upon the gene model allelic variance ( σ2a ). These two cannot simply be added to get total genic variance. One approach in avoiding this problem was to re-visit the derivation of the average allele substitution effect, and to construct a version, ( β f ), that incorporates the effects of the dispersion. Crow and Kimura achieved this[13] : 130–131 using the re-centered allele effects (a•, d•, (-a)• ) discussed previously ["Gene effects re-defined"]. However, this was found subsequently to under-estimate slightly the total Genic variance, and a new variance-based derivation led to a refined version.[36]
The refined version is: β f = { a2 + [(1−f ) / (1 + f )] 2(q − p ) ad + [(1-f ) / (1 + f )] (q − p )2 d2 } (1/2)
Consequently, σ2A(f) = (1 + f ) 2pq βf 2 does now agree with [ (1-f) σ2A(0) + 2f σ2a(0) ] exactly.
Total and partitioned dispersed quasi-dominance variances
The total genic variance is of intrinsic interest in its own right. But, prior to the refinements by Gordon,[36] it had had another important use as well. There had been no extant estimators for the "dispersed" quasi-dominance. This had been estimated as the difference between Sewall Wright's inbred genotypic variance [37] and the total "dispersed" genic variance [see the previous sub-section]. An anomaly appeared, however, because the total quasi-dominance variance appeared to increase early in inbreeding despite the decline in heterozygosity.[14] : 128 : 266
The refinements in the previous sub-section corrected this anomaly.[36] At the same time, a direct solution for the total quasi-dominance variance was obtained, thus avoiding the need for the "subtraction" method of previous times. Furthermore, direct solutions for the amongst-line and within-line partitions of the quasi-dominance variance were obtained also, for the first time. [These have been presented in the section "Dispersion and the genotypic variance".]
Environmental variance
The environmental variance is phenotypic variability, which cannot be ascribed to genetics. This sounds simple, but the experimental design needed to separate the two needs very careful planning. Even the "external" environment can be divided into spatial and temporal components ("Sites" and "Years"); or into partitions such as "litter" or "family", and "culture" or "history". These components are very dependent upon the actual experimental model used to do the research. Such issues are very important when doing the research itself, but in this article on quantitative genetics this overview may suffice.
It is an appropriate place, however, for a summary:
Phenotypic variance = genotypic variances + environmental variances + genotype-environment interaction + experimental "error" variance
i.e., σ2P = σ2G + σ2E + σ2GE + σ2
or σ2P = σ2A + σ2D + σ2I + σ2E + σ2GE + σ2
after partitioning the genotypic variance (G) into component variances "genic" (A), "quasi-dominance" (D), and "epistatic" (I).[51]
The environmental variance will appear in other sections, such as "Heritability" and "Correlated attributes".
Heritability and repeatability
The heritability of a trait is the proportion of the total (phenotypic) variance (σ2 P) that is attributable to genetic variance, whether it be the full genotypic variance, or some component of it. It quantifies the degree to which phenotypic variability is due to genetics: but the precise meaning depends upon which genetical variance partition is used in the numerator of the proportion.[52] Research estimates of heritability have standard errors, just as have all estimated statistics.[53]
Where the numerator variance is the whole Genotypic variance ( σ2G ), the heritability is known as the "broadsense" heritability (H2). It quantifies the degree to which variability in an attribute is determined by genetics as a whole. [See section on the Genotypic variance.]
If only genic variance (σ2A) is used in the numerator, the heritability may be called "narrow sense" (h2). It quantifies the extent to which phenotypic variance is determined by Fisher's substitution expectations variance. Fisher proposed that this narrow-sense heritability might be appropriate in considering the results of natural selection, focusing as it does on change-ability, that is upon "adaptation".[29] He proposed it with regard to quantifying Darwinian evolution.
Recalling that the allelic variance (σ 2a) and the dominance variance (σ 2d) are eu-genetic components of the gene-model [see section on the Genotypic variance], and that σ 2D (the substitution deviations or "quasi-dominance" variance) and covad are due to changing from the homozygote midpoint (mp) to the population mean (G), it can be seen that the real meanings of these heritabilities are obscure. The heritabilities and have unambiguous meaning.
Narrow-sense heritability has been used also for predicting generally the results of artificial selection. In the latter case, however, the broadsense heritability may be more appropriate, as the whole attribute is being altered: not just adaptive capacity. Generally, advance from selection is more rapid the higher the heritability. [See section on "Selection".] In animals, heritability of reproductive traits is typically low, while heritability of disease resistance and production are moderately low to moderate, and heritability of body conformation is high.
Repeatability (r2) is the proportion of phenotypic variance attributable to differences in repeated measures of the same subject, arising from later records. It is used particularly for long-lived species. This value can only be determined for traits that manifest multiple times in the organism's lifetime, such as adult body mass, metabolic rate or litter size. Individual birth mass, for example, would not have a repeatability value: but it would have a heritability value. Generally, but not always, repeatability indicates the upper level of the heritability.[54]
r2 = (s2G + s2PE)/s2P
where s2PE = phenotype-environment interaction = repeatability.
The above concept of repeatability is, however, problematic for traits that necessarily change greatly between measurements. For example, body mass increases greatly in many organisms between birth and adult-hood. Nonetheless, within a given age range (or life-cycle stage), repeated measures could be done, and repeatability would be meaningful within that stage.
Relationship
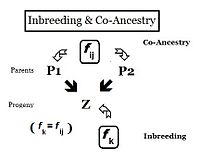
From the heredity perspective, relations are individuals that inherited genes from one or more common ancestors. Therefore, their "relationship" can be quantified on the basis of the probability that they each have inherited a copy of an allele from the common ancestor. In earlier sections, the Inbreeding coefficient has been defined as, "the probability that two same alleles ( A and A, or a and a ) have a common origin"—or, more formally, "The probability that two homologous alleles are autozygous." Previously, the emphasis was on an individual's likelihood of having two such alleles, and the coefficient was framed accordingly. It is obvious, however, that this probability of autozygosity for an individual must also be the probability that each of its two parents had this autozygous allele. In this re-focused form, the probability is called the co-ancestry coefficient for the two individuals i and j ( f ij ). In this form, it can be used to quantify the relationship between two individuals, and may also be known as the coefficient of kinship or the consanguinity coefficient.[13]: 132–143 [14]: 82–92
Pedigree analysis

Pedigrees are diagrams of familial connections between individuals and their ancestors, and possibly between other members of the group that share genetical inheritance with them. They are relationship maps. A pedigree can be analyzed, therefore, to reveal coefficients of inbreeding and co-ancestry. Such pedigrees actually are informal depictions of path diagrams as used in path analysis, which was invented by Sewall Wright when he formulated his studies on inbreeding.[55]: 266–298 Using the adjacent diagram, the probability that individuals "B" and "C" have received autozygous alleles from ancestor "A" is 1/2 (one out of the two diploid alleles). This is the "de novo" inbreeding (ΔfPed) at this step. However, the other allele may have had "carry-over" autozygosity from previous generations, so the probability of this occurring is (de novo complement multiplied by the inbreeding of ancestor A ), that is (1 − ΔfPed ) fA = (1/2) fA . Therefore, the total probability of autozygosity in B and C, following the bi-furcation of the pedigree, is the sum of these two components, namely (1/2) + (1/2)fA = (1/2) (1+f A ) . This can be viewed as the probability that two random gametes from ancestor A carry autozygous alleles, and in that context is called the coefficient of parentage ( fAA ).[13]: 132–143 [14]: 82–92 It appears often in the following paragraphs.
Following the "B" path, the probability that any autozygous allele is "passed on" to each successive parent is again (1/2) at each step (including the last one to the "target" X ). The overall probability of transfer down the "B path" is therefore (1/2)3 . The power that (1/2) is raised to can be viewed as "the number of intermediates in the path between A and X ", nB = 3 . Similarly, for the "C path", nC = 2 , and the "transfer probability" is (1/2)2 . The combined probability of autozygous transfer from A to X is therefore [ fAA (1/2)(nB) (1/2)(nC) ] . Recalling that fAA = (1/2) (1+f A ) , fX = fPQ = (1/2)(nB + nC + 1) (1 + fA ) . In this example, assuming that fA = 0, fX = 0.0156 (rounded) = fPQ , one measure of the "relatedness" between P and Q.
In this section, powers of (1/2) were used to represent the "probability of autozygosity". Later, this same method will be used to represent the proportions of ancestral gene-pools which are inherited down a pedigree [the section on "Relatedness between relatives"].

Cross-multiplication rules
In the following sections on sib-crossing and similar topics, a number of "averaging rules" are useful. These derive from path analysis.[55] The rules show that any co-ancestry coefficient can be obtained as the average of cross-over co-ancestries between appropriate grand-parental and parental combinations. Thus, referring to the adjacent diagram, Cross-multiplier 1 is that fPQ = average of ( fAC, fAD, fBC, fBD ) = (1/4) [fAC + fAD + fBC + fBD ] = fY . In a similar fashion, cross-multiplier 2 states that fPC = (1/2) [ fAC + fBC ]—while cross-multiplier 3 states that fPD = (1/2) [ fAD + fBD ] . Returning to the first multiplier, it can now be seen also to be fPQ = (1/2) [ fPC + fPD ], which, after substituting multipliers 2 and 3, resumes its original form.
In much of the following, the grand-parental generation is referred to as (t-2), the parent generation as (t-1), and the "target" generation as t.
Full-sib crossing (FS)
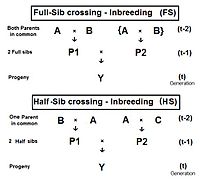
The diagram to the right shows that full sib crossing is a direct application of cross-Multiplier 1, with the slight modification that parents A and B repeat (in lieu of C and D) to indicate that individuals P1 and P2 have both of their parents in common—that is they are full siblings. Individual Y is the result of the crossing of two full siblings. Therefore, fY = fP1,P2 = (1/4) [ fAA + 2 fAB + fBB ] . Recall that fAA and fBB were defined earlier (in Pedigree analysis) as coefficients of parentage, equal to (1/2)[1+fA ] and (1/2)[1+fB ] respectively, in the present context. Recognize that, in this guise, the grandparents A and B represent generation (t-2) . Thus, assuming that in any one generation all levels of inbreeding are the same, these two coefficients of parentage each represent (1/2) [1 + f(t-2) ] .

Now, examine fAB . Recall that this also is fP1 or fP2 , and so represents their generation - f(t-1) . Putting it all together, ft = (1/4) [ 2 fAA + 2 fAB ] = (1/4) [ 1 + f(t-2) + 2 f(t-1) ] . That is the inbreeding coefficient for Full-Sib crossing .[13]: 132–143 [14]: 82–92 The graph to the left shows the rate of this inbreeding over twenty repetitive generations. The "repetition" means that the progeny after cycle t become the crossing parents that generate cycle (t+1 ), and so on successively. The graphs also show the inbreeding for random fertilization 2N=20 for comparison. Recall that this inbreeding coefficient for progeny Y is also the co-ancestry coefficient for its parents, and so is a measure of the relatedness of the two Fill siblings.
Half-sib crossing (HS)
Derivation of the half sib crossing takes a slightly different path to that for Full sibs. In the adjacent diagram, the two half-sibs at generation (t-1) have only one parent in common—parent "A" at generation (t-2). The cross-multiplier 1 is used again, giving fY = f(P1,P2) = (1/4) [ fAA + fAC + fBA + fBC ] . There is just one coefficient of parentage this time, but three co-ancestry coefficients at the (t-2) level (one of them—fBC—being a "dummy" and not representing an actual individual in the (t-1) generation). As before, the coefficient of parentage is (1/2)[1+fA ] , and the three co-ancestries each represent f(t-1) . Recalling that fA represents f(t-2) , the final gathering and simplifying of terms gives fY = ft = (1/8) [ 1 + f(t-2) + 6 f(t-1) ] .[13]: 132–143 [14]: 82–92 The graphs at left include this half-sib (HS) inbreeding over twenty successive generations.
As before, this also quantifies the relatedness of the two half-sibs at generation (t-1) in its alternative form of f(P1, P2) .
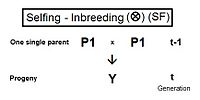
Self fertilization (SF)
A pedigree diagram for selfing is on the right. It is so straightforward it does not require any cross-multiplication rules. It employs just the basic juxtaposition of the inbreeding coefficient and its alternative the co-ancestry coefficient; followed by recognizing that, in this case, the latter is also a coefficient of parentage. Thus, fY = f(P1, P1) = ft = (1/2) [ 1 + f(t-1) ] .[13]: 132–143 [14]: 82–92 This is the fastest rate of inbreeding of all types, as can be seen in the graphs above. The selfing curve is, in fact, a graph of the coefficient of parentage.
Cousins crossings

These are derived with methods similar to those for siblings.[13]: 132–143 [14]: 82–92 As before, the co-ancestry viewpoint of the inbreeding coefficient provides a measure of "relatedness" between the parents P1 and P2 in these cousin expressions.
The pedigree for First Cousins (FC) is given to the right. The prime equation is fY = ft = fP1,P2 = (1/4) [ f1D + f12 + fCD + fC2 ]. After substitution with corresponding inbreeding coefficients, gathering of terms and simplifying, this becomes ft = (1/4) [ 3 f(t-1) + (1/4) [2 f(t-2) + f(t-3) + 1 ]] , which is a version for iteration—useful for observing the general pattern, and for computer programming. A "final" version is ft = (1/16) [ 12 f(t-1) + 2 f(t-2) + f(t-3) + 1 ] .

The Second Cousins (SC) pedigree is on the left. Parents in the pedigree not related to the common Ancestor are indicated by numerals instead of letters. Here, the prime equation is fY = ft = fP1,P2 = (1/4) [ f3F + f34 + fEF + fE4 ]. After working through the appropriate algebra, this becomes ft = (1/4) [ 3 f(t-1) + (1/4) [3 f(t-2) + (1/4) [2 f(t-3) + f(t-4) + 1 ]]] , which is the iteration version. A "final" version is ft = (1/64) [ 48 f(t-1) + 12 f(t-2) + 2 f(t-3) + f(t-4) + 1 ] .

To visualize the pattern in full cousin equations, start the series with the full sib equation re-written in iteration form: ft = (1/4)[2 f(t-1) + f(t-2) + 1 ]. Notice that this is the "essential plan" of the last term in each of the cousin iterative forms: with the small difference that the generation indices increment by "1" at each cousin "level". Now, define the cousin level as k = 1 (for First cousins), = 2 (for Second cousins), = 3 (for Third cousins), etc., etc.; and = 0 (for Full Sibs, which are "zero level cousins"). The last term can be written now as: (1/4) [ 2 f(t-(1+k)) + f(t-(2+k)) + 1] . Stacked in front of this last term are one or more iteration increments in the form (1/4) [ 3 f(t-j) + ... , where j is the iteration index and takes values from 1 ... k over the successive iterations as needed. Putting all this together provides a general formula for all levels of full cousin possible, including Full Sibs. For kth level full cousins, f{k}t = Ιterj = 1k { (1/4) [ 3 f(t-j) + }j + (1/4) [ 2 f(t-(1+k)) + f(t-(2+k)) + 1] . At the commencement of iteration, all f(t-x) are set at "0", and each has its value substituted as it is calculated through the generations. The graphs to the right show the successive inbreeding for several levels of Full Cousins.

For first half-cousins (FHC), the pedigree is to the left. Notice there is just one common ancestor (individual A). Also, as for second cousins, parents not related to the common ancestor are indicated by numerals. Here, the prime equation is fY = ft = fP1,P2 = (1/4) [ f3D + f34 + fCD + fC4 ]. After working through the appropriate algebra, this becomes ft = (1/4) [ 3 f(t-1) + (1/8) [6 f(t-2) + f(t-3) + 1 ]] , which is the iteration version. A "final" version is ft = (1/32) [ 24 f(t-1) + 6 f(t-2) + f(t-3) + 1 ] . The iteration algorithm is similar to that for full cousins, except that the last term is (1/8) [ 6 f(t-(1+k)) + f(t-(2+k)) + 1 ] . Notice that this last term is basically similar to the half sib equation, in parallel to the pattern for full cousins and full sibs. In other words, half sibs are "zero level" half cousins.
There is a tendency to regard cousin crossing with a human-oriented point of view, possibly because of a wide interest in Genealogy. The use of pedigrees to derive the inbreeding perhaps reinforces this "Family History" view. However, such kinds of inter-crossing occur also in natural populations—especially those that are sedentary, or have a "breeding area" that they re-visit from season to season. The progeny-group of a harem with a dominant male, for example, may contain elements of sib-crossing, cousin crossing, and backcrossing, as well as genetic drift, especially of the "island" type. In addition to that, the occasional "outcross" adds an element of hybridization to the mix. It is not panmixia.
Backcrossing (BC)


Following the hybridizing between A and R, the F1 (individual B) is crossed back (BC1) to an original parent (R) to produce the BC1 generation (individual C). [It is usual to use the same label for the act of making the back-cross and for the generation produced by it. The act of back-crossing is here in italics. ] Parent R is the recurrent parent. Two successive backcrosses are depicted, with individual D being the BC2 generation. These generations have been given t indices also, as indicated. As before, fD = ft = fCR = (1/2) [ fRB + fRR ] , using cross-multiplier 2 previously given. The fRB just defined is the one that involves generation (t-1) with (t-2). However, there is another such fRB contained wholly within generation (t-2) as well, and it is this one that is used now: as the co-ancestry of the parents of individual C in generation (t-1). As such, it is also the inbreeding coefficient of C, and hence is f(t-1). The remaining fRR is the coefficient of parentage of the recurrent parent, and so is (1/2) [1 + fR ] . Putting all this together : ft = (1/2) [ (1/2) [ 1 + fR ] + f(t-1) ] = (1/4) [ 1 + fR + 2 f(t-1) ] . The graphs at right illustrate Backcross inbreeding over twenty backcrosses for three different levels of (fixed) inbreeding in the Recurrent parent.
This routine is commonly used in Animal and Plant Breeding programmes. Often after making the hybrid (especially if individuals are short-lived), the recurrent parent needs separate "line breeding" for its maintenance as a future recurrent parent in the backcrossing. This maintenance may be through selfing, or through full-sib or half-sib crossing, or through restricted randomly fertilized populations, depending on the species' reproductive possibilities. Of course, this incremental rise in fR carries-over into the ft of the backcrossing. The result is a more gradual curve rising to the asymptotes than shown in the present graphs, because the fR is not at a fixed level from the outset.
Contributions from ancestral genepools
In the section on "Pedigree analysis", was used to represent probabilities of autozygous allele descent over n generations down branches of the pedigree. This formula arose because of the rules imposed by sexual reproduction: (i) two parents contributing virtually equal shares of autosomal genes, and (ii) successive dilution for each generation between the zygote and the "focus" level of parentage. These same rules apply also to any other viewpoint of descent in a two-sex reproductive system. One such is the proportion of any ancestral gene-pool (also known as 'germplasm') which is contained within any zygote's genotype.
Therefore, the proportion of an ancestral genepool in a genotype is: where n = number of sexual generations between the zygote and the focus ancestor.
For example, each parent defines a genepool contributing to its offspring; while each great-grandparent contributes to its great-grand-offspring.
The zygote's total genepool (Γ) is, of course, the sum of the sexual contributions to its descent.
Relationship through ancestral genepools
Individuals descended from a common ancestral genepool obviously are related. This is not to say they are identical in their genes (alleles), because, at each level of ancestor, segregation and assortment will have occurred in producing gametes. But they will have originated from the same pool of alleles available for these meioses and subsequent fertilizations. [This idea was encountered firstly in the sections on pedigree analysis and relationships.] The genepool contributions [see section above] of their nearest common ancestral genepool(an ancestral node) can therefore be used to define their relationship. This leads to an intuitive definition of relationship which conforms well with familiar notions of "relatedness" found in family-history; and permits comparisons of the "degree of relatedness" for complex patterns of relations arising from such genealogy.
The only modifications necessary (for each individual in turn) are in Γ and are due to the shift to "shared common ancestry" rather than "individual total ancestry". For this, define Ρ (in lieu of Γ); m = number of ancestors-in-common at the node (i.e. m = 1 or 2 only); and an "individual index" k. Thus:
where, as before, n = number of sexual generations between the individual and the ancestral node.
An example is provided by two first full-cousins. Their nearest common ancestral node is their grandparents which gave rise to their two sibling parents, and they have both of these grandparents in common. [See earlier pedigree.] For this case, m=2 and n=2, so for each of them
In this simple case, each cousin has numerically the same Ρ .
A second example might be between two full cousins, but one (k=1) has three generations back to the ancestral node (n=3), and the other (k=2) only two (n=2) [i.e. a second and first cousin relationship]. For both, m=2 (they are full cousins).
and
Notice each cousin has a different Ρ k.
GRC – genepool relationship coefficient
In any pairwise relationship estimation, there is one Ρk for each individual: it remains to average them in order to combine them into a single "Relationship coefficient". Because each Ρ is a fraction of a total genepool, the appropriate average for them is the geometric mean [56][57]: 34–55 This average is their Genepool Relationship Coefficient—the "GRC".
For the first example (two full first-cousins), their GRC = 0.5; for the second case (a full first and second cousin), their GRC = 0.3536.
All of these relationships (GRC) are applications of path-analysis.[55]: 214–298 A summary of some levels of relationship (GRC) follow.
| GRC | Relationship examples |
|---|---|
| 1.00 | full Sibs |
| 0.7071 | Parent ↔ Offspring; Uncle/Aunt ↔ Nephew/Niece |
| 0.5 | full First Cousins; half Sibs; grand Parent ↔ grand Offspring |
| 0.3536 | full Cousins First ↔ Second; full First Cousins {1 remove} |
| 0.25 | full Second Cousins; half First Cousins; full First Cousins {2 removes} |
| 0.1768 | full First Cousin {3 removes}; full Second Cousins {1 remove} |
| 0.125 | full Third Cousins; half Second Cousins; full 1st Cousins {4 removes} |
| 0.0884 | full First Cousins {5 removes}; half Second Cousins {1 remove} |
| 0.0625 | full Fourth Cousins; half Third Cousins |
Resemblances between relatives
These, in like manner to the Genotypic variances, can be derived through either the gene-model ("Mather") approach or the allele-substitution ("Fisher") approach. Here, each method is demonstrated for alternate cases.
Parent-offspring covariance
These can be viewed either as the covariance between any offspring and any one of its parents (PO), or as the covariance between any offspring and the "mid-parent" value of both its parents (MPO).
One-parent and offspring (PO)
This can be derived as the sum of cross-products between parent gene-effects and one-half of the progeny expectations using the allele-substitution approach. The one-half of the progeny expectation accounts for the fact that only one of the two parents is being considered. The appropriate parental gene-effects are therefore the second-stage redefined gene effects used to define the genotypic variances earlier, that is: a″ = 2q(a − qd) and d″ = (q-p)a + 2pqd and also (-a)″ = -2p(a + pd) [see section "Gene effects redefined"]. Similarly, the appropriate progeny effects, for allele-substitution expectations are one-half of the earlier breeding values, the latter being: aAA = 2qa, and aAa = (q-p)a and also aaa = -2pa [see section on "Genotype substitution – Expectations and Deviations"].
Because all of these effects are defined already as deviates from the genotypic mean, the cross-product sum using {genotype-frequency * parental gene-effect * half-breeding-value} immediately provides the allele-substitution-expectation covariance between any one parent and its offspring. After careful gathering of terms and simplification, this becomes cov(PO)A = pqa2 = 1/2 s2A .[13] : 132–141 [14] : 134–147
Unfortunately, the allele-substitution-deviations are usually overlooked, but they have not "ceased to exist" nonetheless! Recall that these deviations are: dAA = -2q2 d, and dAa = 2pq d and also daa = -2p2 d [see section on "Genotype substitution – Expectations and Deviations"]. Consequently, the cross-product sum using {genotype-frequency * parental gene-effect * half-substitution-deviations} also immediately provides the allele-substitution-deviations covariance between any one parent and its offspring. Once more, after careful gathering of terms and simplification, this becomes cov(PO)D = 2p2q2d2 = 1/2 s2D .
It follows therefore that: cov(PO) = cov(PO)A + cov(PO)D = 1/2 s2A + 1/2 s2D , when dominance is not overlooked !
Mid-parent and offspring (MPO)
Because there are many combinations of parental genotypes, there are many different mid-parents and offspring means to consider, together with the varying frequencies of obtaining each parental pairing. The gene-model approach is the most expedient in this case. Therefore, an unadjusted sum of cross-products (USCP)—using all products { parent-pair-frequency * mid-parent-gene-effect * offspring-genotype-mean }—is adjusted by subtracting the {overall genotypic mean}2 as correction factor (CF). After multiplying out all the various combinations, carefully gathering terms, simplifying, factoring and cancelling-out where applicable, this becomes:
cov(MPO) = pq [a + (q-p)d ]2 = pq a2 = 1/2 s2A , with no dominance having been overlooked in this case, as it had been used-up in defining the a.[13] : 132–141 [14] : 134–147
Applications (parent-offspring)
The most obvious application is an experiment that contains all parents and their offspring, with or without reciprocal crosses, preferably replicated without bias, enabling estimation of all appropriate means, variances and covariances, together with their standard errors. These estimated statistics can then be used to estimate the genetic variances. Twice the difference between the estimates of the two forms of (corrected) parent-offspring covariance provides an estimate of s2D; and twice the cov(MPO) estimates s2A. With appropriate experimental design and analysis,[9][49][50] standard errors can be obtained for these genetical statistics as well. This is the basic core of an experiment known as Diallel analysis, the Mather, Jinks and Hayman version of which is discussed in another section.
A second application involves using regression analysis, which estimates from statistics the ordinate (Y-estimate), derivative (regression coefficient) and constant (Y-intercept) of calculus.[9][49][58][59] The regression coefficient estimates the rate of change of the function predicting Y from X, based on minimizing the residuals between the fitted curve and the observed data (MINRES). No alternative method of estimating such a function satisfies this basic requirement of MINRES. In general, the regression coefficient is estimated as the ratio of the covariance(XY) to the variance of the determinator (X). In practice, the sample size is usually the same for both X and Y, so this can be written as SCP(XY) / SS(X), where all terms have been defined previously.[9][58][59] In the present context, the parents are viewed as the "determinative variable" (X), and the offspring as the "determined variable" (Y), and the regression coefficient as the "functional relationship" (ßPO) between the two. Taking cov(MPO) = 1/2 s2A as cov(XY), and s2P / 2 (the variance of the mean of two parents—the mid-parent) as s2X, it can be seen that ßMPO = [1/2 s2A] / [1/2 s2P] = h2 .[60] Next, utilizing cov(PO) = [ 1/2 s2A + 1/2 s2D ] as cov(XY), and s2P as s2X, it is seen that 2 ßPO = [ 2 (1/2 s2A + 1/2 s2D )] / s2P = H2 .
Analysis of epistasis has previously been attempted via an interaction variance approach of the type s2AA , and s2AD and also s2DD. This has been integrated with these present covariances in an effort to provide estimators for the epistasis variances. However, the findings of epigenetics suggest that this may not be an appropriate way to define epistasis.
Siblings covariances
Covariance between half-sibs (HS) is defined easily using allele-substitution methods; but, once again, the dominance contribution has historically been omitted. However, as with the mid-parent/offspring covariance, the covariance between full-sibs (FS) requires a "parent-combination" approach, thereby necessitating the use of the gene-model corrected-cross-product method; and the dominance contribution has not historically been overlooked. The superiority of the gene-model derivations is as evident here as it was for the Genotypic variances.
Half-sibs of the same common-parent (HS)
The sum of the cross-products { common-parent frequency * half-breeding-value of one half-sib * half-breeding-value of any other half-sib in that same common-parent-group } immediately provides one of the required covariances, because the effects used [breeding values—representing the allele-substitution expectations] are already defined as deviates from the genotypic mean [see section on "Allele substitution – Expectations and deviations"]. After simplification. this becomes: cov(HS)A = 1/2 pq a2 = 1/4 s2A .[13] : 132–141 [14] : 134–147 However, the substitution deviations also exist, defining the sum of the cross-products { common-parent frequency * half-substitution-deviation of one half-sib * half-substitution-deviation of any other half-sib in that same common-parent-group }, which ultimately leads to: cov(HS)D = p2 q2 d2 = 1/4 s2D . Adding the two components gives:
cov(HS) = cov(HS)A + cov(HS)D = 1/4 s2A + 1/4 s2D .
Full-sibs (FS)
As explained in the introduction, a method similar to that used for mid-parent/progeny covariance is used. Therefore, an unadjusted sum of cross-products (USCP) using all products—{ parent-pair-frequency * the square of the offspring-genotype-mean }—is adjusted by subtracting the {overall genotypic mean}2 as correction factor (CF). In this case, multiplying out all combinations, carefully gathering terms, simplifying, factoring, and cancelling-out is very protracted. It eventually becomes:
cov(FS) = pq a2 + p2 q2 d2 = 1/2 s2A + 1/4 s2D , with no dominance having been overlooked.[13] : 132–141 [14] : 134–147
Applications (siblings)
The most useful application here for genetical statistics is the correlation between half-sibs. Recall that the correlation coefficient (r) is the ratio of the covariance to the variance [see section on "Associated attributes" for example]. Therefore, rHS = cov(HS) / s2all HS together = [1/4 s2A + 1/4 s2D ] / s2P = 1/4 H2 .[61] The correlation between full-sibs is of little utility, being rFS = cov(FS) / s2all FS together = [1/2 s2A + 1/4 s2D ] / s2P . The suggestion that it "approximates" (1/2 h2) is poor advice.
Of course, the correlations between siblings are of intrinsic interest in their own right, quite apart from any utility they may have for estimating heritabilities or genotypic variances.
It may be worth noting that [ cov(FS) − cov(HS)] = 1/4 s2A . Experiments consisting of FS and HS families could utilize this by using intra-class correlation to equate experiment variance components to these covariances [see section on "Coefficient of relationship as an intra-class correlation" for the rationale behind this].
The earlier comments regarding epistasis apply again here [see section on "Applications (Parent-offspring"].
Selection
Basic principles

Selection operates on the attribute (phenotype), such that individuals that equal or exceed a selection threshold (zP) become effective parents for the next generation. The proportion they represent of the base population is the selection pressure. The smaller the proportion, the stronger the pressure. The mean of the selected group (Ps) is superior to the base-population mean (P0) by the difference called the selection differential (S). All these quantities are phenotypic. To "link" to the underlying genes, a heritability (h2) is used, fulfilling the role of a coefficient of determination in the biometrical sense. The expected genetical change—still expressed in phenotypic units of measurement—is called the genetic advance (ΔG), and is obtained by the product of the selection differential (S) and its coefficient of determination (h2). The expected mean of the progeny (P1) is found by adding the genetic advance (ΔG) to the base mean (P0). The graphs to the right show how the (initial) genetic advance is greater with stronger selection pressure (smaller probability). They also show how progress from successive cycles of selection (even at the same selection pressure) steadily declines, because the Phenotypic variance and the Heritability are being diminished by the selection itself. This is discussed further shortly.
Thus .[14] : 1710–181 and .[14] : 1710–181
The narrow-sense heritability (h2) is usually used, thereby linking to the genic variance (σ2A) . However, if appropriate, use of the broad-sense heritability (H2) would connect to the genotypic variance (σ2G); and even possibly an allelic heritability [ h2eu = (σ2a) / (σ2P) ] might be contemplated, connecting to (σ2a ). [See section on Heritability.]
To apply these concepts before selection actually takes place, and so predict the outcome of alternatives (such as choice of selection threshold, for example), these phenotypic statistics are re-considered against the properties of the Normal Distribution, especially those concerning truncation of the superior tail of the Distribution. In such consideration, the standardized selection differential (i)″ and the standardized selection threshold (z)″ are used instead of the previous "phenotypic" versions. The phenotypic standard deviate (σP(0)) is also needed. This is described in a subsequent section.
Therefore, ΔG = (i σP) h2, where (i σP(0)) = S previously.[14] : 1710–181

The text above noted that successive ΔG declines because the "input" [the phenotypic variance ( σ2P )] is reduced by the previous selection.[14]: 1710–181 The heritability also is reduced. The graphs to the left show these declines over ten cycles of repeated selection during which the same selection pressure is asserted. The accumulated genetic advance (ΣΔG) has virtually reached its asymptote by generation 6 in this example. This reduction depends partly upon truncation properties of the Normal Distribution, and partly upon the heritability together with meiosis determination ( b2 ). The last two items quantify the extent to which the truncation is "offset" by new variation arising from segregation and assortment during meiosis.[14] : 1710–181 [27] This is discussed soon, but here note the simplified result for undispersed random fertilization (f = 0).
Thus : σ2P(1) = σ2P(0) [1 − i ( i-z) 1/2 h2], where i ( i-z) = K = truncation coefficient and 1/2 h2 = R = reproduction coefficient[14]: 1710–181 [27] This can be written also as σ2P(1) = σ2P(0) [1 − K R ], which facilitates more detailed analysis of selection problems.
Here, i and z have already been defined, 1/2 is the meiosis determination (b2) for f=0, and the remaining symbol is the heritability. These are discussed further in following sections. Also notice that, more generally, R = b2 h2. If the general meiosis determination ( b2 ) is used, the results of prior inbreeding can be incorporated into the selection. The phenotypic variance equation then becomes:
σ2P(1) = σ2P(0) [1 − i ( i-z) b2 h2].
The Phenotypic variance truncated by the selected group ( σ2P(S) ) is simply σ2P(0) [1 − K], and its contained genic variance is (h20 σ2P(S) ). Assuming that selection has not altered the environmental variance, the genic variance for the progeny can be approximated by σ2A(1) = ( σ2P(1) − σ2E) . From this, h21 = ( σ2A(1) / σ2P(1) ). Similar estimates could be made for σ2G(1) and H21, or for σ2a(1) and h2eu(1) if required.
Alternative ΔG
The following rearrangement is useful for considering selection on multiple attributes (characters). It starts by expanding the heritability into its variance components. ΔG = i σP ( σ2A / σ2P ) . The σP and σ2P partially cancel, leaving a solo σP. Next, the σ2A inside the heritability can be expanded as (σA × σA), which leads to :

ΔG = i σA ( σA / σP ) = i σA h .
Corresponding re-arrangements could be made using the alternative heritabilities, giving ΔG = i σG H or ΔG = i σa heu.
Polygenic Adaptation Models in Population Genetics
This traditional view of adaptation in quantitative genetics provides a model for how the selected phenotype changes over time, as a function of the selection differential and heritability. However it does not provide insight into (nor does it depend upon) any of the genetic details - in particular, the number of loci involved, their allele frequencies and effect sizes, and the frequency changes driven by selection. This, in contrast, is the focus of work on polygenic adaptation[62] within the field of population genetics. Recent studies have shown that traits such as height have evolved in humans during the past few thousands of years as a result of small allele frequency shifts at thousands of variants that affect height.[63][64][65]
Background
Standardized selection – the normal distribution
The entire base population is outlined by the normal curve[59]: 78–89 to the right. Along the Z axis is every value of the attribute from least to greatest, and the height from this axis to the curve itself is the frequency of the value at the axis below. The equation for finding these frequencies for the "normal" curve (the curve of "common experience") is given in the ellipse. Notice it includes the mean (μ) and the variance (σ2). Moving infinitesimally along the z-axis, the frequencies of neighbouring values can be "stacked" beside the previous, thereby accumulating an area that represents the probability of obtaining all values within the stack. [That's integration from calculus.] Selection focuses on such a probability area, being the shaded-in one from the selection threshold (z) to the end of the superior tail of the curve. This is the selection pressure. The selected group (the effective parents of the next generation) include all phenotype values from z to the "end" of the tail.[66] The mean of the selected group is μs, and the difference between it and the base mean (μ) represents the selection differential (S). By taking partial integrations over curve-sections of interest, and some rearranging of the algebra, it can be shown that the "selection differential" is S = [ y (σ / Prob.)] , where y is the frequency of the value at the "selection threshold" z (the ordinate of z).[13]: 226–230 Rearranging this relationship gives S / σ = y / Prob., the left-hand side of which is, in fact, selection differential divided by standard deviation—that is the standardized selection differential (i). The right-side of the relationship provides an "estimator" for i—the ordinate of the selection threshold divided by the selection pressure. Tables of the Normal Distribution[49] : 547–548 can be used, but tabulations of i itself are available also.[67]: 123–124 The latter reference also gives values of i adjusted for small populations (400 and less),[67]: 111–122 where "quasi-infinity" cannot be assumed (but was presumed in the "Normal Distribution" outline above). The standardized selection differential (i) is known also as the intensity of selection.[14]: 174, 186
Finally, a cross-link with the differing terminology in the previous sub-section may be useful: μ (here) = "P0" (there), μS = "PS" and σ2 = "σ2P".
Meiosis determination – reproductive path analysis


The meiosis determination (b2) is the coefficient of determination of meiosis, which is the cell-division whereby parents generate gametes. Following the principles of standardized partial regression, of which path analysis is a pictorially oriented version, Sewall Wright analyzed the paths of gene-flow during sexual reproduction, and established the "strengths of contribution" (coefficients of determination) of various components to the overall result.[27][37] Path analysis includes partial correlations as well as partial regression coefficients (the latter are the path coefficients). Lines with a single arrow-head are directional determinative paths, and lines with double arrow-heads are correlation connections. Tracing various routes according to path analysis rules emulates the algebra of standardized partial regression.[55]
The path diagram to the left represents this analysis of sexual reproduction. Of its interesting elements, the important one in the selection context is meiosis. That's where segregation and assortment occur—the processes that partially ameliorate the truncation of the phenotypic variance that arises from selection. The path coefficients b are the meiosis paths. Those labeled a are the fertilization paths. The correlation between gametes from the same parent (g) is the meiotic correlation. That between parents within the same generation is rA. That between gametes from different parents (f) became known subsequently as the inbreeding coefficient.[13]: 64 The primes ( ' ) indicate generation (t-1), and the unprimed indicate generation t. Here, some important results of the present analysis are given. Sewall Wright interpreted many in terms of inbreeding coefficients.[27][37]
The meiosis determination (b2) is 1/2 (1+g) and equals 1/2 (1 + f(t-1)) , implying that g = f(t-1).[68] With non-dispersed random fertilization, f(t-1)) = 0, giving b2 = 1/2, as used in the selection section above. However, being aware of its background, other fertilization patterns can be used as required. Another determination also involves inbreeding—the fertilization determination (a2) equals 1 / [ 2 ( 1 + ft ) ] . Also another correlation is an inbreeding indicator—rA = 2 ft / ( 1 + f(t-1) ), also known as the coefficient of relationship. [Do not confuse this with the coefficient of kinship—an alternative name for the co-ancestry coefficient. See introduction to "Relationship" section.] This rA re-occurs in the sub-section on dispersion and selection.
These links with inbreeding reveal interesting facets about sexual reproduction that are not immediately apparent. The graphs to the right plot the meiosis and syngamy (fertilization) coefficients of determination against the inbreeding coefficient. There it is revealed that as inbreeding increases, meiosis becomes more important (the coefficient increases), while syngamy becomes less important. The overall role of reproduction [the product of the previous two coefficients—r2] remains the same.[69] This increase in b2 is particularly relevant for selection because it means that the selection truncation of the Phenotypic variance is offset to a lesser extent during a sequence of selections when accompanied by inbreeding (which is frequently the case).
Genetic drift and selection
The previous sections treated dispersion as an "assistant" to selection, and it became apparent that the two work well together. In quantitative genetics, selection is usually examined in this "biometrical" fashion, but the changes in the means (as monitored by ΔG) reflect the changes in allele and genotype frequencies beneath this surface. Referral to the section on "Genetic drift" brings to mind that it also effects changes in allele and genotype frequencies, and associated means; and that this is the companion aspect to the dispersion considered here ("the other side of the same coin"). However, these two forces of frequency change are seldom in concert, and may often act contrary to each other. One (selection) is "directional" being driven by selection pressure acting on the phenotype: the other (genetic drift) is driven by "chance" at fertilization (binomial probabilities of gamete samples). If the two tend towards the same allele frequency, their "coincidence" is the probability of obtaining that frequencies sample in the genetic drift: the likelihood of their being "in conflict", however, is the sum of probabilities of all the alternative frequency samples. In extreme cases, a single syngamy sampling can undo what selection has achieved, and the probabilities of it happening are available. It is important to keep this in mind. However, genetic drift resulting in sample frequencies similar to those of the selection target does not lead to so drastic an outcome—instead slowing progress towards selection goals.
Correlated attributes
Upon jointly observing two (or more) attributes (e.g. height and mass), it may be noticed that they vary together as genes or environments alter. This co-variation is measured by the covariance, which can be represented by " cov " or by θ.[43] It will be positive if they vary together in the same direction; or negative if they vary together but in opposite direction. If the two attributes vary independently of each other, the covariance will be zero. The degree of association between the attributes is quantified by the correlation coefficient (symbol r or ρ ). In general, the correlation coefficient is the ratio of the covariance to the geometric mean [70] of the two variances of the attributes.[59] : 196–198 Observations usually occur at the phenotype, but in research they may also occur at the "effective haplotype" (effective gene product) [see Figure to the right]. Covariance and correlation could therefore be "phenotypic" or "molecular", or any other designation which an analysis model permits. The phenotypic covariance is the "outermost" layer, and corresponds to the "usual" covariance in Biometrics/Statistics. However, it can be partitioned by any appropriate research model in the same way as was the phenotypic variance. For every partition of the covariance, there is a corresponding partition of the correlation. Some of these partitions are given below. The first subscript (G, A, etc.) indicates the partition. The second-level subscripts (X, Y) are "place-keepers" for any two attributes.

The first example is the un-partitioned phenotype.
The genetical partitions (a) "genotypic" (overall genotype),(b) "genic" (substitution expectations) and (c) "allelic" (homozygote) follow.
(a)
(b)
(c)
With an appropriately designed experiment, a non-genetical (environment) partition could be obtained also.
Underlying causes of correlation
There are several different ways that phenotypic correlation can arise. Study design, sample size, sample statistics, and other factors can influence the ability to distinguish between them with more or less statistical confidence. Each of these have different scientific significance, and are relevant to different fields of work.
Direct causation
One phenotype may directly affect another phenotype, by influencing development, metabolism, or behavior.
Genetic pathways
A common gene or transcription factor in the biological pathways for the two phenotypes can result in correlation.
Metabolic pathways
The metabolic pathways from gene to phenotype are complex and varied, but the causes of correlation amongst attributes lie within them.
Developmental and environmental factors
Multiple phenotypes may be affected by the same factors. For example, there are many phenotypic attributes correlated with age, and so height, weight, caloric intake, endocrine function, and more all have a correlation. A study looking for other common factors must rule these out first.
Correlated genotypes and selective pressures
Differences between subgroups in a population, between populations, or selective biases can mean that some combinations of genes are overrepresented compared with what would be expected. While the genes may not have a significant influence on each other, there may still be a correlation between them, especially when certain genotypes are not allowed to mix. Populations in the process of genetic divergence or having already undergone it can have different characteristic phenotypes,[71] which means that when considered together, a correlation appears. Phenotypic qualities in humans that predominantly depend on ancestry also produce correlations of this type. This can also be observed in dog breeds where several physical features make up the distinctness of a given breed, and are therefore correlated.[72] Assortative mating, which is the sexually selective pressure to mate with a similar phenotype, can result in genotypes remaining correlated more than would be expected.[73]
See also
- Artificial selection
- Diallel cross
- Douglas Scott Falconer
- Ewens's sampling formula
- Experimental evolution
- QST
- Genetic architecture
- Genetic distance
- Heritability
- Ronald Fisher
Footnotes and references
- ^ Anderberg, Michael R. (1973). Cluster analysis for applications. New York: Academic Press.
- ^ Mendel, Gregor (1866). "Versuche über Pflanzen Hybriden". Verhandlungen Naturforschender Verein in Brünn. iv.
- ^ a b c Mendel, Gregor (1891). "Experiments in plant hybridisation". J. Roy. Hort. Soc. (London). XXV. Translated by Bateson, William: 54–78.
- ^ The Mendel G.; Bateson W. (1891) paper, with additional comments by Bateson, is reprinted in: Sinnott E.W.; Dunn L.C.; Dobzhansky T. (1958). "Principles of genetics"; New York, McGraw-Hill: 419-443. Footnote 3, page 422 identifies Bateson as the original translator, and provides the reference for that translation.
- ^ A QTL is a region in the DNA genome that effects, or is associated with, quantitative phenotypic traits.
- ^ Watson, James D.; Gilman, Michael; Witkowski, Jan; Zoller, Mark (1998). Recombinant DNA (Second (7th printing) ed.). New York: W.H. Freeman (Scientific American Books). ISBN 978-0-7167-1994-6.
- ^ Jain, H. K.; Kharkwal, M. C., eds. (2004). Plant Breeding - Mendelian to molecular approaches. Boston Dordecht London: Kluwer Academic Publishers. ISBN 978-1-4020-1981-4.
- ^ a b c d Fisher, R. A. (1918). "The Correlation between Relatives on the Supposition of Mendelian Inheritance". Transactions of the Royal Society of Edinburgh. 52 (2): 399–433. doi:10.1017/s0080456800012163. S2CID 181213898. Archived from the original on 8 October 2020. Retrieved 7 September 2020.
- ^ a b c d e f g Steel, R. G. D.; Torrie, J. H. (1980). Principles and procedures of statistics (2 ed.). New York: McGraw-Hill. ISBN 0-07-060926-8.
- ^ Other symbols are sometimes used, but these are common.
- ^ The allele effect is the average phenotypic deviation of the homozygote from the mid-point of the two contrasting homozygote phenotypes at one locus, when observed over the infinity of all background genotypes and environments. In practice, estimates from large unbiased samples substitute for the parameter.
- ^ The dominance effect is the average phenotypic deviation of the heterozygote from the mid-point of the two homozygotes at one locus, when observed over the infinity of all background genotypes and environments. In practice, estimates from large unbiased samples substitute for the parameter.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah Crow, J. F.; Kimura, M. (1970). An introduction to population genetics theory. New York: Harper & Row.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al Falconer, D. S.; Mackay, Trudy F. C. (1996). Introduction to quantitative genetics (Fourth ed.). Harlow: Longman. ISBN 978-0582-24302-6.
- William G Hill; Trudy F C Mackay (August 2004). "D. S. Falconer and Introduction to Quantitative Genetics". Genetics. 167 (4): 1529–1536. doi:10.1093/genetics/167.4.1529. PMC 1471025. PMID 15342495.
- ^ Mendel commented on this particular tendency for F1 > P1, i.e., evidence of hybrid vigour in stem length. However, the difference may not be significant. (The relationship between the range and the standard deviation is known [Steel and Torrie (1980): 576], permitting an approximate significance test to be made for this present difference.)
- ^ Richards, A. J. (1986). Plant breeding systems. Boston: George Allen & Unwin. ISBN 0-04-581020-6.
- ^ Jane Goodall Institute. "Social structure of chimpanzees". Chimp Central. Archived from the original on 3 July 2008. Retrieved 20 August 2014.
- ^ Gordon, Ian L. (2000). "Quantitative genetics of allogamous F2: an origin of randomly fertiliized populations". Heredity. 85: 43–52. doi:10.1046/j.1365-2540.2000.00716.x. PMID 10971690.
- ^ An F2 derived by self fertilizing F1 individuals (an autogamous F2), however, is not an origin of a randomly fertilized population structure. See Gordon (2001).
- ^ Castle, W. E. (1903). "The law of heredity of Galton and Mendel and some laws governing race improvement by selection". Proceedings of the American Academy of Arts and Sciences. 39 (8): 233–242. doi:10.2307/20021870. hdl:2027/hvd.32044106445109. JSTOR 20021870.
- ^ Hardy, G. H. (1908). "Mendelian proportions in a mixed population". Science. 28 (706): 49–50. Bibcode:1908Sci....28...49H. doi:10.1126/science.28.706.49. PMC 2582692. PMID 17779291.
- ^ Weinberg, W. (1908). "Über den Nachweis der Verebung beim Menschen". Jahresh. Verein F. Vaterl. Naturk, Württem. 64: 368–382.
- ^ Usually in science ethics, a discovery is named after the earliest person to propose it. Castle, however, seems to have been overlooked: and later when re-found, the title "Hardy Weinberg" was so ubiquitous it seemed too late to update it. Perhaps the "Castle Hardy Weinberg" equilibrium would be a good compromise?
- ^ a b Gordon, Ian L. (1999). "Quantitative genetics of intraspecies hybrids". Heredity. 83 (6): 757–764. doi:10.1046/j.1365-2540.1999.00634.x. PMID 10651921.
- ^ Gordon, Ian L. (2001). "Quantitative genetics of autogamous F2". Hereditas. 134 (3): 255–262. doi:10.1111/j.1601-5223.2001.00255.x. PMID 11833289.
- ^ Wright, S. (1917). "The average correlation within subgroups of a population". J. Wash. Acad. Sci. 7: 532–535.
- ^ a b c d e f g Wright, S. (1921). "Systems of mating. I. The biometric relations between parent and offspring". Genetics. 6 (2): 111–123. doi:10.1093/genetics/6.2.111. PMC 1200501. PMID 17245958.
- ^ Sinnott, Edmund W.; Dunn, L. C.; Dobzhansky, Theodosius (1958). Principles of genetics. New York: McGraw-Hill.
- ^ a b c d e Fisher, R. A. (1999). The genetical theory of natural selection (variorum ed.). Oxford: Oxford University Press. ISBN 0-19-850440-3.
- ^ a b Cochran, William G. (1977). Sampling techniques (Third ed.). New York: John Wiley & Sons.
- ^ This is outlined subsequently in the genotypic variances section.
- ^ Both are used commonly.
- ^ See the earlier citations.
- ^ Allard, R. W. (1960). Principles of plant breeding. New York: John Wiley & Sons.
- ^ a b This is read as "σ 2p and/or σ 2q". As p and q are complementary, σ 2p ≡ σ 2q and σ 2p = σ 2q.
- ^ a b c d e f g h i Gordon, I.L. (2003). "Refinements to the partitioning of the inbred genotypic variance". Heredity. 91 (1): 85–89. doi:10.1038/sj.hdy.6800284. PMID 12815457.
- ^ a b c d e f g h i j Wright, Sewall (1951). "The genetical structure of populations". Annals of Eugenics. 15 (4): 323–354. doi:10.1111/j.1469-1809.1949.tb02451.x. PMID 24540312.
- ^ Remember that the issue of auto/allo -zygosity can arise only for homologous alleles (that is A and A, or a and a), and not for non-homologous alleles (A and a), which cannot possibly have the same allelic origin.
- ^ It is common to use "α" rather than "β" for this quantity (e.g. in the references already cited). The latter is used herein in order to minimize any confusion with "a", which frequently occurs also within these same equations.
- ^ a b c d Mather, Kenneth; Jinks, John L. (1971). Biometrical genetics. Vol. 26 (2 ed.). London: Chapman & Hall. pp. 349–364. doi:10.1038/hdy.1971.47. ISBN 0-412-10220-X. PMID 5285746. S2CID 46065232.
{{cite book}}:|journal=ignored (help) - ^ In Mather's terminology, the fraction in front of the letter is a part of the label for the component.
- ^ In each line of these equations, the components are presented in the same order. Therefore, vertical comparison by component gives the definition of each in various forms. The Mather components have been translated thereby into Fisherian symbols: thus facilitating their comparison. The translation has been derived formally as well. See Gordon 2003.
- ^ a b Covariance is the co-variability between two sets of data. Similarly to the variance, it is based on a sum of cross-products (SCP) instead of a SS. From this, it is clear therefore that the variance is but a special form of the covariance.
- ^ Hayman, B. I. (1960). "The theory and analysis of the diallel cross. III". Genetics. 45 (2): 155–172. doi:10.1093/genetics/45.2.155. PMC 1210041. PMID 17247915.
- ^ It has been observed that when p = q, or when d = 0, β [= a+(q-p)d] "reduces" to a. In such circumstances, σ2A = σ2a—but only numerically. They still have not become the one and the same identity. This would be a similar non sequitur to that noted earlier for the "substitution deviations" being regarded as the "dominance" for the gene-model.
- ^ Supporting citations have been given already in the previous sections.
- ^ Fisher did note that these residuals arose through the effects of dominance: but he refrained from defining them as the "dominance variance". (See the foregoing citations.) Refer again to the earlier discussions herein.
- ^ While considering origins of terms: Fisher also proposed the word "variance" for this measure of variability. See Fisher (1999), p. 311 and Fisher (1918).
- ^ a b c d Snedecor, George W.; Cochran, William G. (1967). Statistical methods (Sixth ed.). Ames: Iowa State University Press. ISBN 0-8138-1560-6.
- ^ a b c Kendall, M. G.; Stuart, A. (1958). The advanced theory of statistics. Volume 1 (2nd ed.). London: Charles Griffin.
- ^ It is common practice not to have a subscript on the experimental "error" variance.
- ^ In biometry, it is a variance-ratio in which a part is expressed as a fraction of the whole: that is, a coefficient of determination. Such coefficients are used particularly in regression analysis. A standardized version of regression analysis is path analysis. Here, standardizing means that the data were first divided by their own experimental standard errors to unify the scales for all attributes. This genetical usage is another major appearance of coefficients of determination.
- ^ Gordon, I. L.; Byth, D. E.; Balaam, L. N. (1972). "Variance of heritability ratios estimated from phenotypic variance components". Biometrics. 28 (2): 401–415. doi:10.2307/2556156. JSTOR 2556156. PMID 5037862.
- ^ Dohm, M. R. (2002). "Repeatability estimates do not always set an upper limit to heritibility". Functional Ecology. 16 (2): 273–280. Bibcode:2002FuEco..16..273M. doi:10.1046/j.1365-2435.2002.00621.x.
- ^ a b c d Li, Ching Chun (1977). Path analysis - a Primer (Second printing with Corrections ed.). Pacific Grove: Boxwood Press. ISBN 0-910286-40-X.
- ^ the square-root of their product
- ^ Moroney, M.J. (1956). Facts from figures (third ed.). Harmondsworth: Penguin Books.
- ^ a b Draper, Norman R.; Smith, Harry (1981). Applied regression analysis (Second ed.). New York: John Wiley & Sons. ISBN 0-471-02995-5.
- ^ a b c d Balaam, L. N. (1972). Fundamentals of biometry. London: George Allen & Unwin. ISBN 0-04-519008-9.
- ^ In the past, both forms of parent-offspring covariance have been applied to this task of estimating h2, but, as noted in the sub-section above, only one of them (cov(MPO)) is actually appropriate. The cov(PO) is useful, however, for estimating H2 as seen in the main text following.
- ^ Note that texts that ignore the dominance component of cov(HS) erroneously suggest that rHS "approximates" ( 1/4 h2 ).
- ^ Pritchard, Jonathan K.; Pickrell, Joseph K.; Coop, Graham (23 February 2010). "The genetics of human adaptation: hard sweeps, soft sweeps, and polygenic adaptation". Current Biology. 20 (4): R208–215. Bibcode:2010CBio...20.R208P. doi:10.1016/j.cub.2009.11.055. ISSN 1879-0445. PMC 2994553. PMID 20178769.
- ^ Turchin, Michael C.; Chiang, Charleston W. K.; Palmer, Cameron D.; Sankararaman, Sriram; Reich, David; Genetic Investigation of ANthropometric Traits (GIANT) Consortium; Hirschhorn, Joel N. (September 2012). "Evidence of widespread selection on standing variation in Europe at height-associated SNPs". Nature Genetics. 44 (9): 1015–1019. doi:10.1038/ng.2368. ISSN 1546-1718. PMC 3480734. PMID 22902787.
- ^ Berg, Jeremy J.; Coop, Graham (August 2014). "A population genetic signal of polygenic adaptation". PLOS Genetics. 10 (8): e1004412. doi:10.1371/journal.pgen.1004412. ISSN 1553-7404. PMC 4125079. PMID 25102153.
- ^ Field, Yair; Boyle, Evan A.; Telis, Natalie; Gao, Ziyue; Gaulton, Kyle J.; Golan, David; Yengo, Loic; Rocheleau, Ghislain; Froguel, Philippe (11 November 2016). "Detection of human adaptation during the past 2000 years". Science. 354 (6313): 760–764. Bibcode:2016Sci...354..760F. doi:10.1126/science.aag0776. ISSN 0036-8075. PMC 5182071. PMID 27738015.
- ^ Theoretically, the tail is infinite, but in practice there is a quasi-end.
- ^ a b Becker, Walter A. (1967). Manual of procedures in quantitative genetics (Second ed.). Pullman: Washington State University.
- ^ Notice that this b2 is the coefficient of parentage (fAA) of Pedigree analysis re-written with a "generation level" instead of an "A" inside the parentheses.
- ^ There is a small "wobble" arising from the fact that b2 alters one generation behind a2—examine their inbreeding equations.
- ^ Estimated as the square-root of their product.
- ^ "Reproductive Isolation". Understanding Evolution. Berkeley. 16 April 2021.
- ^ Serres-Armero, A; Davis, BW; Povolotskaya, IS; Morcillo-Suarez, C; Plassais, J; Juan, D; Ostrander, EA; Marques-Bonet, T (May 2021). "Copy number variation underlies complex phenotypes in domestic dog breeds and other canids". Genome Research. 31 (5): 762–774. doi:10.1101/gr.266049.120. PMC 8092016. PMID 33863806.
- ^ Jiang, Yuexin; Bolnick, Daniel I.; Kirkpatrick, Mark (2013). "Assortative mating in animals" (PDF). The American Naturalist. 181 (6): E125 – E138. doi:10.1086/670160. hdl:2152/31270. PMID 23669548. S2CID 14484725.
Further reading
- Falconer DS & Mackay TFC (1996). Introduction to Quantitative Genetics, 4th Edition. Longman, Essex, England.
- Caballero, A (2020) Quantitative Genetics. Cambridge University Press.
- Lynch M & Walsh B (1998). Genetics and Analysis of Quantitative Traits. Sinauer, Sunderland, MA.
- Roff DA (1997). Evolutionary Quantitative Genetics. Chapman & Hall, New York.
- Seykora, Tony. Animal Science 3221 Animal Breeding. Tech. Minneapolis: University of Minnesota, 2011. Print.
External links
- The Breeder's Equation
- Quantitative Genetics Resources by Michael Lynch and Bruce Walsh, including the two volumes of their textbook, Genetics and Analysis of Quantitative Traits and Evolution and Selection of Quantitative Traits.
- Resources by Nick Barton et al.. from the textbook, Evolution.
- The G-Matrix Online

















![{\textstyle [p^{2}(1-f)+pf]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f1f42f5a9c30f57d018ee039f24e662ebeafb72)

![{\textstyle [q^{2}(1-f)+qf]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03c693d0435f960d467b31a0d257d1ac8c647390)












![{\displaystyle {\begin{aligned}G_{f}&=a(q-p)+[2pqd-f(2pqd)]\\&=a(p-q)+(1-f)2pqd\\&=G_{0}-f\ 2pqd\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b62dfeae280dc4f4e334a3478d8481ca3b464b)





















![{\displaystyle \sigma _{t}^{2}=p_{g}q_{g}\left[1-\left(1-\Delta f\right)^{t}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e55f249d313eb204b0aad0fdd43789c5c9162df)











![{\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17a24c2fb8d160fe93430b166097b4cc095d60ad)


![{\displaystyle \left(1-f\right)\left[p_{0}+q_{0}\right]^{2}=\left(1-f\right)\left[p_{0}^{2}+q_{0}^{2}\right]+\left(1-f\right)\left[2p_{0}q_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/991c1f0545c26c29bd5dc324a08fd084d599990d)


![{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c68483dd44cb95ca503376fb095d8cba86179be)
![{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087333e8a96612e7fb9b5c5da00ac55b23584278)






![{\textstyle p_{0}^{2}-f\left[p_{0}\left(1-q_{0}\right)-p_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f31341803ce88db781b4f1c1fdc94e7a19a81488)








![{\displaystyle m_{t}=1-\left[{\frac {2N\ {^{\mathsf {islands}}\Delta f_{t}}}{\left(2N-1\right)\ {^{\mathsf {islands}}\Delta f_{t}+1}}}\right]^{\tfrac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a63b7a6c5b54623d679828146c2530268c3193c)




![{\displaystyle \beta _{A}=q\ \left[a+\left(q-p\right)d\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a8cb74299e659b83fc9cc07fe4056495b026ed)
![{\displaystyle \beta _{a}=-\ p\left[a+\left(q-p\right)d\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aedc78c372df5239f7f7ef9b28f19c8766374064)








![{\displaystyle {\begin{aligned}\sigma _{G}^{2}&=2pq\left[a+(q-p)d\right]^{2}+\left(2pq\right)^{2}d^{2}\\&=\sigma _{A}^{2}+\sigma _{D}^{2}\\&=\left[\left(\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}\right)\right]+\left[2pq\ \sigma _{d}^{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c33eb29c59ac7394562c287f1b65e8d3fea9a8d7)

![{\displaystyle \sigma _{G_{f}}^{2}=\left(1-f\right)\sigma _{G_{0}}^{2}+f\ \sigma _{G_{1}}^{2}+f\left(1-f\right)\left[G_{0}-G_{1}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baa52231a4dac02644cad91c045a5eb586f2502d)






![{\displaystyle \sigma _{G_{f}}^{2}=\left(1-f\right)\left[\sigma _{A_{0}}^{2}+\sigma _{D_{0}}^{2}\right]+f\ \left(4pq\ a^{2}\right)+f\ \left(1-f\right)\left[2pq\ d\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8e77c382254b7230fcc0cb09f36d8a056cba93a)






![{\displaystyle {\begin{aligned}H^{2}&={\frac {\sigma _{G}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\sigma _{A}^{2}+\sigma _{D}^{2}}{\sigma _{P}^{2}}}\\&={\frac {\left[\sigma _{a}^{2}+\sigma _{d}^{2}+cov_{ad}\right]+\sigma _{D}^{2}}{\sigma _{P}^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76a552eecb057ebb771e98bc0b94b39ed29de3c3)




















