Practical Applications of a SDMS (Scientific Data Management System)
Sommaire
La projection cylindrique équidistante, encore appelée projection équirectangulaire ou projection géographique, est un type de projection cartographique très simple attribué à Marinus de Tyr vers 100 ap. J.-C.[1].
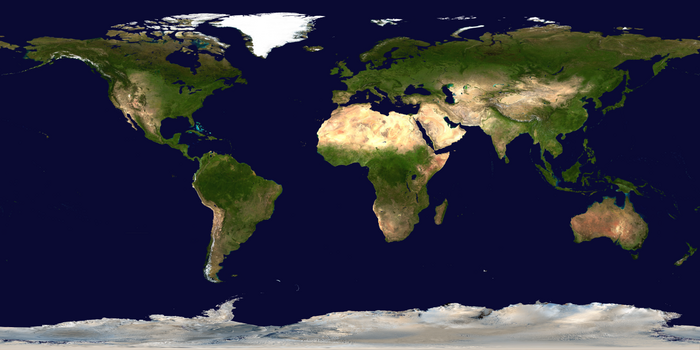
Description
La projection consiste à considérer les coordonnées polaires de latitude et longitude comme des coordonnées cartésiennes. En ce sens, on parle parfois de « non-projection ».
Cependant la transformation effectuée se définit (partiellement) comme une projection de la surface du globe sur la surface d'un cylindre, dont l'axe se confond avec l'axe des pôles et contient les origines des vecteurs de projection. Les méridiens sont alors projetés sur des lignes verticales espacées de manière égale, et les parallèles sont aussi projetés sur des lignes horizontales équidistantes (espacement horizontal constant). Ce dernier point différencie cette projection de la projection de Mercator. De plus, contrairement à la projection de Mercator, la projection cylindrique équidistante n'est pas conforme. Elle n'est pas non plus équivalente, mais aphylactique (elle conserve les distances le long des méridiens, d'où le nom « projection cylindrique équidistante »).
Définition mathématique

Les équations suivantes déterminent les coordonnées x et y d'un point sur une carte à partir de sa latitude φ et de sa longitude λ lorsque le point (φ0, λ0) est au centre de la carte (fixé, par convention, à l'origine) :
avec
- λ est la longitude;
- φ est la latitude;
- x est la position sur l'axe horizontal de la carte;
- y est la position sur l'axe vertical de la carte;
- (φ0, λ0) est au centre de la carte
- R est le rayon de la terre
est une constante ; la transformation est donc bilinéaire. Cette constante se traduit par une absence de déformation à proximité du parallèle central (c'est-à-dire de latitude φ0), et minimise globalement la déformation.
La projection plate carrée correspond au cas particulier où la carte est centrée sur l'équateur (, ):
De manière plus restrictive, il s'agit d'une projection cylindrique équidistante du globe entier.
Projection inverse
avec
- x est la position sur l'axe horizontal de la carte;
- y est la position sur l'axe vertical de la carte;
- λ est la longitude;
- φ est la latitude;
- (φ0, λ0) est au centre de la carte
Utilisation

En particulier, la plate carrée est cependant devenue de-facto un standard car le rendu ne dépend plus du centre choisi. Cependant, on observe un étirement horizontal croissant lorsqu'on s'éloigne de l'équateur. À cause des distorsions introduites par cette projection, elle est de peu d'utilité pour la navigation ou les cartes cadastrales.
Pour la navigation, on lui préfère aujourd'hui la projection de Mercator, qui bien que cylindrique également et ne conservant pas les distances le long des parallèles différents, ni le long des méridiens (ni donc non plus les surfaces), permet de conserver localement un facteur d'échelle quasi constant permettant de conserver les angles (sur une surface pas trop grande et à condition de ne pas trop s'approcher des pôles) et la forme des objets pas trop grands vus à leur verticale : la simplicité de cette dernière fait que la projection de Mercator est privilégiée par les sites web de géolocalisation (Géoportail, Google Earth…).
Pour les cartes cadastrales, on préfère les projections coniques conformes sur une plage de latitude limitée qui respecte les distances, les angles, les formes et le facteur d'échelle (sur des étendues pas trop grandes) et conserve les parallèles (cependant une légère distorsion des méridiens peut s'observer à mesure qu'on s'éloigne du centre de la carte), mais ces projections ne permettent pas de produire une carte du monde entier mais seulement d'un hémisphère à l'exception des zones polaires.
Pour les zones polaires ou de latitude très élevée (au delà de 80° de latitude nord ou sud), une projection conique non conforme permettrait de conserver les distances et surfaces, mais pas les angles, et les méridiens convergent vers le centre de la carte qui doit couper le long d'un méridien choisi arbitrairement ; on lui préfère alors une projection sur le plan horizontal tangent à la sphère et orthogonal à l'axe polaire et sur une étendue limitée en latitudes (une légère altération des distances peut s'observer avec un allongement des distances et surfaces à mesure qu'on s'éloigne du pôle, mais les déformations angulaires sont moins précises et ce type de carte convient encore à la navigation) ou bien une projection centrée au pôle sur un cône dans l'axe polaire passant par un parallèle de latitude moyenne représenté par un cercle sur la carte, et là aussi avec un choix arbitraire du méridien pour l'orienter (cette fois l'altération des distances s'observe à mesure qu'on s'éloigne du cercle parallèle choisi, vers le centre de la carte au pôle ou vers les bords aux latitudes les plus faibles). Cependant il n'y a pas d'application cadastrale dans les zones des pôles géographiques qui sont soit en mer arctique au nord, soit en zone internationale antarctique au sud où, pour les autres utilisations, une projection azimutale plane centrée au pôle est suffisante aux cartes topographiques et installations locales.
Notes et références
- Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 5-8, (ISBN 0-226-76747-7).
Voir aussi
Articles connexes
- Liste de projections cartographiques
- Projection équivalente cylindrique de Lambert
- Projection de Mercator
Liens externes
- (en) The blue marble : land surface, ocean color and sea ice : réalisation de la projection équirectangulaire du globe terrestre à partir d'images satellites.
- (en) Tableau d'exemples et propriétés de toutes les projections communes, par radicalcartography.net.
- (en) Projection équirectangulaire panoramique, sur le wiki PanoTools.
- (en) Equidistant Cylindrical (Plate Caree) dans proj4


























