Potency and safety analysis of hemp-derived delta-9 products: The hemp vs. cannabis demarcation problem
Contents
In physics, spherical multipole moments are the coefficients in a series expansion of a potential that varies inversely with the distance R to a source, i.e., as Examples of such potentials are the electric potential, the magnetic potential and the gravitational potential.
For clarity, we illustrate the expansion for a point charge, then generalize to an arbitrary charge density Through this article, the primed coordinates such as refer to the position of charge(s), whereas the unprimed coordinates such as refer to the point at which the potential is being observed. We also use spherical coordinates throughout, e.g., the vector has coordinates where is the radius, is the colatitude and is the azimuthal angle.
Spherical multipole moments of a point charge

The electric potential due to a point charge located at is given by where is the distance between the charge position and the observation point and is the angle between the vectors and . If the radius of the observation point is greater than the radius of the charge, we may factor out 1/r and expand the square root in powers of using Legendre polynomials This is exactly analogous to the axial multipole expansion.
We may express in terms of the coordinates of the observation point and charge position using the spherical law of cosines (Fig. 2)
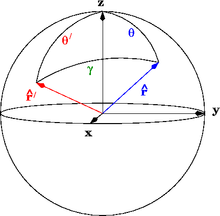
Substituting this equation for into the Legendre polynomials and factoring the primed and unprimed coordinates yields the important formula known as the spherical harmonic addition theorem where the functions are the spherical harmonics. Substitution of this formula into the potential yields
which can be written as where the multipole moments are defined
As with axial multipole moments, we may also consider the case when the radius of the observation point is less than the radius of the charge. In that case, we may write which can be written as where the interior spherical multipole moments are defined as the complex conjugate of irregular solid harmonics
The two cases can be subsumed in a single expression if and are defined to be the lesser and greater, respectively, of the two radii and ; the potential of a point charge then takes the form, which is sometimes referred to as Laplace expansion
Exterior spherical multipole moments
It is straightforward to generalize these formulae by replacing the point charge with an infinitesimal charge element and integrating. The functional form of the expansion is the same. In the exterior case, where , the result is: where the general multipole moments are defined
Note
The potential Φ(r) is real, so that the complex conjugate of the expansion is equally valid. Taking of the complex conjugate leads to a definition of the multipole moment which is proportional to Yℓm, not to its complex conjugate. This is a common convention, see molecular multipoles for more on this.
Interior spherical multipole moments
Similarly, the interior multipole expansion has the same functional form. In the interior case, where , the result is: with the interior multipole moments defined as
Interaction energies of spherical multipoles
A simple formula for the interaction energy of two non-overlapping but concentric charge distributions can be derived. Let the first charge distribution be centered on the origin and lie entirely within the second charge distribution . The interaction energy between any two static charge distributions is defined by
The potential of the first (central) charge distribution may be expanded in exterior multipoles where represents the exterior multipole moment of the first charge distribution. Substitution of this expansion yields the formula
Since the integral equals the complex conjugate of the interior multipole moments of the second (peripheral) charge distribution, the energy formula reduces to the simple form
For example, this formula may be used to determine the electrostatic interaction energies of the atomic nucleus with its surrounding electronic orbitals. Conversely, given the interaction energies and the interior multipole moments of the electronic orbitals, one may find the exterior multipole moments (and, hence, shape) of the atomic nucleus.
Special case of axial symmetry
The spherical multipole expansion takes a simple form if the charge distribution is axially symmetric (i.e., is independent of the azimuthal angle ). By carrying out the integrations that define and , it can be shown the multipole moments are all zero except when . Using the mathematical identity the exterior multipole expansion becomes where the axially symmetric multipole moments are defined In the limit that the charge is confined to the -axis, we recover the exterior axial multipole moments.
Similarly the interior multipole expansion becomes where the axially symmetric interior multipole moments are defined In the limit that the charge is confined to the -axis, we recover the interior axial multipole moments.










































































