Laboratory demand management strategies: An overview
Sisukord
| See artikkel räägib reaalarvude geomeetrilisest kujutamisest; reaalarvude ruumi kohta vaata artiklit Reaalsirge |



Arvtelg ehk arvsirge on reaalarvude kujutamiseks kasutatav sirge, millel on fikseeritud arvu null kujutis ja arvu üks kujutis.[1] Sellega on ühtlasi fikseeritud ka kõikide teiste reaalarvude kujutised (punktipaaridele, mille punktide kaugus on võrdne, vastavad reaalarvude paarid, mille arvude vahe absoluutväärtus on võrdne).
Matemaatilises kõnepruugis samastatakse reaalarvud sageli arvsirge punktidega ning reaalarvude hulgast koos loomuliku järjestusega kõneldakse kui reaalsirgest.
Arvsirge konstrueerimine
Arvsirge saamiseks valime kõigepealt algpunkti , mis on arvu 0 kujutis, ning suuna (positiivse suuna), mis vastab arvude kasvamise suunale. Tavaliselt joonestatakse arvsirge horisontaalsena ning suurematele arvudele seatakse vastavusse parempoolsemad punktid. Kui sirge on kujutatud vertikaalsena, siis on suuremate arvude kujutised tavaliselt kõrgemal. Joonisel saab kujutada ainult osa sirgest; tavaliselt joonistatakse sirge katkestuskohale, mille suunas arvud kasvavad, noolepea, mis on suunatud arvude kasvamise suunas.
Mis tahes punktile arvsirgel vastab parajasti üks reaalarv ning ümberpöördult: igale reaalarvule vastab parajasti üks punkt arvteljel, nii et vektor on suunatud positiivses suunas, kui , vastassuunas, kui , ja see punkt on , kui ; ning vektori pikkus on absoluutväärtus . Selle, et igale reaalarvule vastab mingi punkt arvsirgel, tagab pidevuse aksioom tänapäeva geomeetria aksiomaatikas.
Et saada tavaline arvsirge ehk lineaarne arvsirge, kanname sirgele valitud võrdsetel kaugustel negatiivsed vasakule. Sellega on valitud arvsirge skaala (ühiklõik). Joonisel markeeritakse tavaliselt ainult täisarvudele vastavad punktid. Täisarvude vahelised vahemikud täidame ülejäänud reaalarvudega.
Arvsirge näitlikustab ühemõõtmelist eukleidilist ruumi. Arvude järjestusele vastab punktide loomulik järjestus sirgel.
Arvsirge joonise rakendused
Arvsirget kasutatakse sageli kõigi reaalarvude hulga kujutamiseks ja funktsioonide graafikute joonestamiseks. Arvsirge lõikudena kujutatakse intervalle. Arvsirget kasutatakse ka liitmise ja lahutamise õpetamisel, eriti tehete puhul negatiivsete arvudega. Samuti kasutatakse arvsirget võrratussüsteemide lahendamisel ning tehete puhul reaalarvude hulga alamhulkadega.
Ajalugu
Arvsirge kasutuselevõtjaks peetakse inglise matemaatikut John Wallist.
Arvsirge laiendused
Kui lisada sirgele otspunktid +∞ ja -∞, saame laiendatud arvsirge.
Kui lisame arvsirgele tasandil ristuva sirge, saame konstrueerida komplekstasandi, mille puhul tasandiga seatakse üksühesesse vastavusse kompleksarvude hulk. Arvsirge on sellisel juhul komplekstasandi reaaltelg.
Arvsirge modifikatsioonid
Eksponentsiaalse arvsirge ehk logaritmilise skaalaga arvsirge puhul vastavad etteantud kaugusele punktide vahel ühesugused proportsioonid arvude vahel. Eksponentsiaalsel arvsirgel on kujutatud ainult positiivsed reaalarvud.
Saab konstrueerida ka teistsuguseid arvsirgeid.
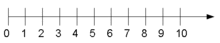
Arvkiirel on kujutatud ainult mittenegatiivsed arvud.
Vaata ka
- Komplekstasand
- Lõik
- Suunatud lõik
- Ühikringjoon
- Descartesi ristkoordinaadid
- Arv
- Koordinaattelg
- Imaginaartelg
Viited
- ↑ Ü. Kaasik, Matemaatikaleksikon (2002)
Välislingid
- Arvsirge saidil matemaatika.edu.ee
- Arvtelg, KAE Kool



























