Knowledge Base Wiki

	Ouça o artigo (info); noicon
	Este áudio foi criado a partir da revisão datada de 26 de janeiro de 2017 e pode não refletir mudanças posteriores ao artigo (ajuda).
	Mais artigos audíveis

Moda é uma das medidas de altura de um conjunto de dados, assim como a média e a mediana. Ela pode ser definida em moda amostral e populacional.

Em relação à primeira delas, a moda amostral de um conjunto de dados trata do valor que ocorre com maior frequência ou o valor mais comum em um conjunto de dados.^[1] Moda é especialmente útil quando os valores ou as observações não são numéricos, casos em que a média e a mediana não podem ser definidas. Por exemplo, a moda da amostra {maçã, banana, laranja, laranja, laranja, pêssego} é laranja.^[2] Moda amostral não é necessariamente única como média ou mediana. Amostras que possuem uma moda são chamadas unimodais. Por exemplo, a amostra {1, 2, 3, 5, 5, 6, 7} tem moda 5. Amostras que possuem duas modas são chamadas bimodais. Por exemplo, a amostra {1, 2, 3, 5, 5, 6, 6} tem modas 5 e 6. Amostras que possuem várias modas são chamadas multimodais. Por exemplo, a amostra {1, 2, 3, 5, 5, 6, 6, 7, 7} tem modas 5, 6 e 7. Amostras que não possuem moda são chamadas amodais. Por exemplo, a amostra {1, 3, 2, 5, 7, 6} não tem moda.^[3]

Já a moda populacional de uma distribuição de probabilidade discreta é o valor $x$ , em que a função massa de probabilidade atinge o valor máximo. Em outras palavras, é o valor que é mais provável de ser amostrado. Moda populacional de uma distribuição de probabilidade contínua é o valor $x$ , em que a função densidade de probabilidade atinge o valor máximo. Em outras palavras, é o valor que está no pico. Moda populacional também não é necessariamente única, uma vez que a função massa de probabilidade ou a função densidade de probabilidade podem ter o mesmo valor máximo em vários pontos $x_{1},x_{2}\dots$ . O caso extremo ocorre nas distribuições uniformes, em que todos os valores ocorrem com igual frequência.

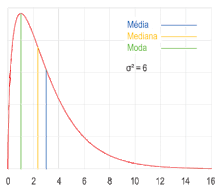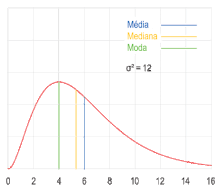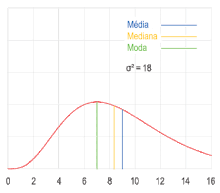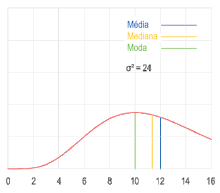
De acordo com a definição acima, máximos globais são modas. Quando uma função densidade de probabilidade tem vários máximos locais, é comum referir-se a todos os máximos locais como modos de distribuição. Tal distribuição contínua é chamada multimodal (em oposição a unimodal). Em distribuições unimodais simétricas como a distribuição normal ou distribuição gaussiana (distribuição cuja função densidade de probabilidade forma a curva em forma de sino quando representada graficamente), a média, a mediana e a moda coincidem. Em amostras extraídas de distribuições simétricas, a média pode ser a estimativa da moda populacional. É importante lembrar que o valor expresso como maioria em um conjunto de dados não necessariamente representa o valor da moda estatística.^[4]

História de como surgiu a palavra moda na matemática

O termo "moda" tem origem em 1895 com Karl Pearson, influenciado pela expressão "estar na moda" usada para objetos muito utilizados pela sociedade como um modelo de carro, uma peça de roupa, um tipo de celular, entre outros utensílios que deem ideia de frequência.^[5]^[6]^[7] Se no cotidiano moda significa muito usado, em estatística moda significa o valor mais frequente em um conjunto de dados.

De acordo com W. Allen Wallis e Harry V. Roberts, no livro Curso de Estatística, há uma referência antiga ao conceito no cerco dos plateus e dos atenienses pelos peloponésios e pelos beócios. No inverno de 428 a.C., os plateus e os atenienses sitiados pelos peloponésios e pelos beócios construíram escadas para escapar pelas muralhas inimigas. Para construir escadas da altura das muralhas inimigas, muitos plateus e atenienses contaram as camadas de tijolos. Mesmo que houvesse erros, a maioria dos sitiados haveria de ter acertado as contagens. Isto é, o grande número de contagens haveria de ser confiável.^[5]

Moda amostral

Ilustração do cálculo da moda de uma população. Para a população {1, 7, 4, 6, 5, 5, 3, 5}, a moda é 5.

Uma amostra pode ser unimodal (uma moda), bimodal (duas modas), multimodal (várias modas) e amodal (nenhuma moda).^[3] Determinadas distribuições patológicas como a distribuição de Cantor não apresentam moda definida. Em uma votação em que a quantidade de votos determina a vitória, um resultado unimodal determina o vencedor enquanto que um valor multimodal exige o desempate. A amostra é chamada homogênea quando possui apenas uma moda e heterogênea quando possui mais de uma moda.^[8]

Em estatística, moda como média e mediana é uma medida de posição, de localização ou de tendência central que mostra a frequência dos dados. Geralmente ordena-se os elementos de um conjunto de dados e conclui-se que a moda é o elemento com maior repetição. ^[9]

Moda em conjunto de dados com elementos repetidos é o valor que ocorre com maior frequência ou o valor mais comum em um conjunto de dados.^[1]^[10]

Sejam os conjuntos $S_{i}$ com $i=1,2,3$ .

Para $S_{1}=\{1,1,1,1,1,1,1\}$ , a moda é $1$ .

Para $S_{2}=\{1,1,2,2,3,4\}$ , as modas são $1$ e $2$ .

Para $S_{3}=\{1,1,2,2,3,3,4,4\}$ , as modas são $1,2,3$ e $4$ .^[11]

Moda é útil quando um ou dois valores ocorrem com maior frequência em um conjunto de dados. Entretanto, a moda nada acrescenta em termos de descrição dos dados quando todos ou quase todos os valores ocorrem aproximadamente com a mesma frequência. (p.23)^[12] Se nenhum valor ocorre com maior frequência em um conjunto de dados, então todos os valores que ocorrem com a maior frequência são chamados valores modais. (p.22)^[13]

Sejam os conjuntos $S'_{i}$ com $i=1,2.$

Para $S'_{1}=\{1,2,3,4,5,6,7\}$ , não há moda.

Para $S'_{2}=\{1,2,3,4,5,6,...\}$ , não há moda.^[11]

Comparação entre média, mediana e moda


Medida	Descrição	Exemplo	Resultado	Principal característica	Principal limitação
Média aritmética	Soma dos valores dividido pelo número de valores de um conjunto de dados.^[14]	${\frac {1+2+2+3+4+7+9}{7}}$	4	Reflete cada valor da amostra.^[15]	É influenciada por valores extremos.^[15]
Mediana	Valor que separa a metade maior e a metade menor de um conjunto de dados.^[16]^[17]	1, 2, 2, 3, 4, 7, 9	3	É menos sensível aos valores extremamente altos ou baixos de uma amostra.^[15]	É difícil de determinar para grandes amostras.^[15]
Moda	Valor que ocorre com maior frequência em um conjunto de dados.^[1]	1, 2, 2, 3, 4, 7, 9	2	Representa o valor típico ou o valor com maior frequência em um ponto.^[15]	Não existe para certos conjuntos de dados.^[15]

Utilizações

Diferente da média e da mediana, a moda é aplicada aos dados nominais. Isto é, quando não há valores numéricos.^[18]^[19] Por exemplo, qual a nota modal de um determinado grupo de estudantes em uma determinada disciplina?

Notas	Número de estudantes
A	3
B	15
C	10
D	9
E	8

A nota modal é B, porque é a nota com maior frequência na amostra.^[20]

Propriedades

Se a variável aleatória ou se cada valor da amostra for submetido a uma transformação linear que substitua $X$ por $aX+b$ , a média, a mediana e a moda mudam também: ${\begin{array}{l}media(aX+b)=a\cdot media(X)+b,\\mediana(aX+b)=a\cdot mediana(X)+b,\\moda(aX+b)=a\cdot moda(X)+b.\end{array}}$
Entretanto, se houver uma transformação monótona arbitrária em geral a moda muda de acordo com a transformação. Por exemplo, se $X$ for substituído por $exp(X)$ , a moda muda de $m$ para $exp(m)$ e a média não muda da mesma maneira.
Com exceção de pequenas amostras, a moda não é sensível a valores discrepantes (outliers) como leituras experimentais falsas, ocasionais ou raras. Enquanto a média é muito sensível, a mediana é bastante robusta na presença de valores atípicos. ^[21]

Intervalo de confiança

Embora comum, é falsa a crença que não é possível obter uma informação sobre variabilidade da população a partir de uma única observação $x$ e que um intervalo de confiança de comprimento finito para média e / ou variância não são possíveis.

É possível para uma distribuição unimodal desconhecida estimar o intervalo de confiança para a moda com uma amostra de tamanho 1.^[22] Isso foi mostrado primeiramente por Abbot and Rosenblatt e ampliado por Blachman^[23] e Machol.^[24] O intervalo de confiança pode ser sharpened se a distribuição pode ser assumida como sendo simétrica. É ainda possível sharpen o intervalo se a distribuição é normalmente distribuída.

Seja o intervalo de confiança $1-\alpha$ . Então, os intervalos de confiança para as variáveis gerais, simétricas e normalmente distribuídas respectivamente são $X\pm ({\frac {2}{\alpha }}-1)|X-\theta |$ , $X\pm ({\frac {1}{\alpha }}-1)|X-\theta |$ e $X\pm ({\frac {0,484}{\alpha }}-1)|X-\theta |$ , em que $X$ é a variável aleatória, $\theta$ é a moda e $|\cdot |$ é o valor absoluto.

Essas estimativas são conservadoras. Os intervalos de confiança para a moda no nível de 90% dada por esses estimadores são

O intervalo de confiança de 95% para uma variável normalmente distribuída é dado por $X\pm 10,7|X-\theta |$ , lembrando que média e a moda coincidem se as variáveis são normalmente distribuídas.

O limite de 95% para uma variável normalmente distribuída tem sido melhorado e é conhecido como $X\pm 9,68|X-\theta |$ .^[25] O limite para um intervalo de confiança de 99% é $X\pm 48,39|X-\theta |$ .

De acordo com Machol, dada uma densidade simétrica conhecida sobre 0 e dado um valor da amostra único $(x)$ , os intervalos de confiança de 90% da média da população são:^[24] $x\pm 5|x-\nu |$ , em que $\nu$ é a mediana da população.

Se a forma precisa da distribuição não for conhecida, mas for simétrica sobre 0, então $P(X-k|X-a|\leq \mu \leq X+k|X-a|)\geq 1-{\frac {1}{1+k}}$ , em que $X$ é a variável, $\mu$ é a média da população e $a$ e $k$ são números reais arbitrários.

Também é possível estimar o intervalo de confiança para o desvio padrão a partir de uma única observação se a distribuição é simétrica em 0.^[26] Para uma distribuição normal com uma variância desconhecida um ponto de dado único $(x)$ , os intervalos de confiança de 90%, 95% e 99% para o desvio padrão são $[0,8|X|]$ , $[0,17|X|]$ e $[0,70|X|]$ . Esses intervalos podem ser reduzidos se a média for conhecida por ser limitada por um múltiplo do desvio padrão.

Se a distribuição for conhecida por ser normal, então é possível estimar o intervalo de confiança para a média e a variância a partir de um valor simples.^[27] Os intervalos de confiança de 90% são $X-23,3|X|\leq \mu \leq X+23,3|X|$ e $\sigma \leq 10|X|$ .

Os intervalos de confiança podem ser estimados para qualquer intervalo escolhido. Esse método não é limitado para distribuições normais, mas pode ser usado para qualquer distribuição conhecida.

Estimadores da moda para dados agrupados

Quando não há acesso aos dados originais mas apenas uma tabela que agrupa os dados em classes de uma variável quantitativa existem vários procedimentos para o cálculo da moda. Os três cálculos de moda mais conhecidos são a moda bruta, a moda de King e a moda de Czuber.^[28]

Moda bruta

Moda bruta é o ponto médio da classe de maior frequência. Seja o conjunto $C$ das alturas de um determinado grupo de pessoas.

Altura (cm)	Número de pessoas (frequência)
161 – 170	6
171 – 180	10
181 – 190	3

No conjunto $C$ , as alturas são as classes. A classe modal é o intervalo entre 171 e 180, com frequência 10.

Então, a moda será definida por $Mo={\frac {l^{*}+L^{*}}{2}}$ , em que $Mo$ é a moda, $l^{*}$ é o limite inferior da classe modal e $L^{*}$ é o limite superior da classe modal.

Portanto, a moda será ${\frac {171+180}{2}}=175,5$ .^[29]

Moda de King

Moda de King considera as classes adjacentes à classe modal. Seja o mesmo conjunto $C$ das alturas do mesmo grupo de pessoas. A amplitude da classe modal é 9, pois a diferença entre 171 e 180 é 9 (assim como ocorre com os intervalos entre 161 e 170 e entre 181 e 190). As classes adjacentes à classe modal são o intervalo entre 161 e 170, com frequência 6, e o intervalo entre 181 e 190, com frequência 3. ^[29]

Então, a moda será definida por $Mo_{King}=l^{*}+{\Bigg [}c\times {\Bigg (}{\frac {F_{post}}{F_{ant}+F_{post}}}{\Bigg )}{\Bigg ]}$ , em que $l^{*}$ é o limite inferior da classe modal, $c$ é a amplitude da classe modal, $F_{post}$ é a frequência de classe posterior a classe modal e $F_{ant}$ é a frequência de classe anterior a classe modal.

Portanto, a moda será $Mo_{King}=171+{\Bigg [}9\times {\Bigg (}{\frac {3}{6+3}}{\Bigg )}{\Bigg ]}=171+3=174$ .^[29]

Moda de Czuber

Moda de Czuber considera as classes adjacentes à classe modal e a própria classe modal. Seja o mesmo conjunto $C$ das alturas do mesmo grupo de pessoas.

Então, a moda será definida por $Mo_{Czuber}=l^{*}+{\Bigg [}c\times {\Bigg (}{\frac {F_{modal}-F_{ant}}{2\times F_{modal}-F_{ant}-F_{post}}}{\Bigg )}{\Bigg ]}$ , em que $l^{*}$ é o limite inferior da classe modal, $c$ é a amplitude da classe modal, $F_{post}$ é a frequência da classe posterior a classe modal, $F_{ant}$ é a frequência da classe anterior a classe modal e $F_{modal}$ é a frequência da classe modal.

Portanto, a moda será $Mo_{Czuber}=171+{\Bigg [}9\times {\Bigg (}{\frac {10-6}{2\times 10-6-3}}{\Bigg )}{\Bigg ]}\cong 171+3,3\cong 174,3$ .^[29]

Moda populacional

Distribuições unimodais

A diferença entre a média e a moda da distribuição contínua unimodal é limitada pelo desvio padrão multiplicado pela raiz quadrada de três.^[30] Em termos matemáticos, ${\frac {|{\text{média}}-{\text{moda}}|}{\text{desvio padrão}}}\leq {\sqrt {3}}$ , em que $|\cdot |$ é o valor absoluto. Inclusive, a fórmula também é a regra de Pearson ou o primeiro coeficiente de assimetria.^[31]

A diferença entre a moda e a mediana tem o mesmo limite.^[30] Em termos matemáticos, ${\frac {|{\text{mediana}}-{\text{moda}}|}{\text{desvio padrão}}}\leq {\sqrt {3}}$ .

Para uma distribuição unimodal, a mediana e a média estão dentro dos ${\sqrt {3/5}}\approx 0,7746$ desvios-padrão de cada um.^[32] Em termos matemáticos, ${\frac {\left|{\text{mediana}}-{\text{média}}\right|}{\text{desvio padrão}}}\leq {\sqrt {\frac {3}{5}}}$ .

Existe uma relação similar para a mediana e a moda, que estão dentro dos ${\sqrt {3}}\approx 1,732$ desvios-padrão de cada um.^[30] Em termos matemáticos, ${\frac {\left|{\text{mediana}}-\mathrm {moda} \right|}{\text{desvio padrão}}}\leq {\sqrt {3}}$ .^[30]

Distribuições distorcidas

Assim como a média e a mediana, a moda expressa em um único número uma informação importante sobre uma variável aleatória ou uma população. O valor numérico da moda coincide com o valor numérico da média e da mediana em distribuições simétricas unimodais como distribuições normais (se a média, a mediana e a moda forem extraídas de uma distribuição simétrica, a média da amostra pode ser usada como estimativa da moda da população). O valor numérico da moda difere do valor número da média e da mediana em distribuições muito distorcidas.^[13]

Um exemplo de uma distribuição distorcida é a renda pessoal. Enquanto muitas pessoas são muito pobres, poucas pessoas são muito ricas (dentre elas, muitas são extremamente ricas).^[33]

Uma classe de distribuições que pode ser arbitrariamente distorcida é dada pela distribuição log-normal. Ela é obtida pela transformação da variável aleatória $X$ com distribuição normal pela variável aleatória $Y=e^{X}$ . ^[34]Então, o logaritmo da variável aleatória $Y$ é normalmente distribuído. Se a média $\mu$ de $X$ for 0, a mediana de $Y$ será 1 independente do desvio padrão $\theta$ de $X$ . Como $X$ tem distribuição simétrica, a mediana será sempre 0. Como a transformação de $X$ para $Y$ é monótona, a mediana $e^{0}=1$ para $Y$ .^[34]

Quando $X$ tem desvio padrão $\theta =0,25$ , a distribuição $Y$ é fracamente distorcida. Usando as fórmulas para a distribuição log-normal, é possível encontrar:

${\begin{array}{rlll}{\text{média}}&=e^{\mu +{\frac {\sigma ^{2}}{2}}}&=e^{0+{\frac {0,25^{2}}{2}}}&\approx 1,032\\{\text{moda}}&=e^{\mu -\sigma ^{2}}&=e^{0-0,25^{2}}&\approx 0,939\\{\text{mediana}}&=e^{\mu }&=e^{0}&=1\end{array}}$

Isto é, a mediana é cerca de um terço da distância entre a média e a moda.^[35]

Quando $X$ tem desvio padrão $\theta =1$ , a distribuição $Y$ é fortemente distorcida. Usando as fórmulas para a distribuição log-normal, é possível encontrar:

${\begin{array}{rlll}{\text{média}}&=e^{\mu +{\frac {\sigma ^{2}}{2}}}&=e^{0+{\frac {1^{2}}{2}}}&\approx 1,649\\{\text{moda}}&=e^{\mu -\sigma ^{2}}&=e^{0-1^{2}}&\approx 0,368\\{\text{mediana}}&=e^{\mu }&=e^{0}&=1\end{array}}$

Isto é, a regra de Pearson não é válida.^[35]

Condição de Van Zwet

Derivada de Van Zwet é uma desigualdade que fornece condições suficientes para assegurar a desigualdade ${\text{moda}}\leq {\text{mediana}}\leq {\text{média}}$ .^[36] Tem-se que $F({\text{mediana}}-x)+F({\text{mediana}}+x)\geq 1$ para todos os $x$ , em que $F$ é a função de distribuição cumulativa da distribuição.^[37]

Informática

Densidade Kernel. Moda também pode ser calculada por meio da estimativa de densidade Kernel, que ofusca amostras pontuais para produzir uma estimativa contínua de uma função densidade de probabilidade que pode fornecer uma estimativa da moda.^[38]

Algoritmo em MATLAB. O exemplo seguinte de código MATLAB ou Octave computa a moda de uma amostra usando derivadas discretas.^[39]

X = sort(x);
indices   =  find(diff([X; realmax]) > 0); % os índices em que valores repetidos mudança
[modeL,i] =  max (diff([0; indices]));     % maior comprimento persistência de valores repetidos
mode      =  X(indices(i));

O algoritmo coloca a amostra em ordem crescente e calcula a derivada discreta da amostra em ordem crescente. Depois ele procura os índices nos quais a derivada é positiva. Em seguira, ele calcula a derivada discreta deste conjunto de índices, e, finalmente, avalia a amostra classificada no ponto em que ocorre esse máximo, o que corresponde ao último membro do estiramento dos valores repetidos.^[39]

Algoritmo em Pascal. Em informática, é possível criar um software que descubra a moda de uma lista de valores em um algoritmo (Pascal):

PROGRAM calcular_moda;

CONST
    n = 20;

VAR
    moda : array [1..n] of real;
    c : array [1..n] of integer;
    i, j, m, cont, a : integer;

BEGIN
    cont := 0;
    WRITE('Quantos números possui a lista');
    READLN(a);
    FOR i := 1 TO a DO
        BEGIN
            WRITE('N', i, ' = ');
            READLN(moda[i]);
            c[i] := 0;
        END;
    FOR i := 1 TO a DO
         BEGIN
              FOR j := 1 TO a DO
                  BEGIN
                       IF((moda[i] = moda[j]) AND (i <> j))THEN
                                   c[i] := c[i] + 1;
                       IF((c[i] = c[j]) AND (i <> j) AND (moda[i] = moda[j]))THEN
                                c[i] := 0;
                  END;
         END;
     FOR i := 1 TO a DO
         BEGIN
              IF(c[i] = 0)THEN
                         moda[i] := 0;
         END;
     FOR i := 1 TO a DO
         BEGIN
              IF(moda[i] <> 0)THEN
                    cont := cont + 1;
         END;
         FOR m := 1 TO (cont DIV 2) DO

         BEGIN
              FOR i := 1 TO a DO
                  BEGIN
                       FOR j := 1 TO a DO
                           BEGIN
                                IF((moda[i] = moda[j]) AND (i <> j))THEN
                                            c[i] := c[i] + 1;
                                IF((c[i] = c[j]) AND (i <> j) AND (moda[i] = moda[j]))THEN
                                         c[i] := 0;
                           END;
                                IF(c[i] = 0)THEN
                                        moda[i] := 0;
                  END;
         END;
     FOR i := 1 TO a DO
         BEGIN
              IF(moda[i] <> 0)THEN
                         WRITELN('Moda = ', moda[i]);
         END;
    READLN;
END.

O mesmo código em C

#include <stdio.h>
#include <conio.h>
#define n 20

int main(){
	float moda[n];
	int c [n];
	int i, j, m, cont, a;
	
	cont = 0;
	printf("Quantos números possui a lista ");
	scanf("%d",&a);
	for (i = 1; i <= a; i++)
	{
		printf("N %d = ", i);
		scanf("%f",&moda[i]);
		c[i] = 0;
	}
	for(i=1;i<=a;i++)
	{
		for(j=1;j<=a;j++)
		{
			if((moda[i] == moda[j]) && (i != j))
				c[i] = c[i] + 1;
			if((c[i] == c[j]) && (i != j) && (moda[i] == moda[j]))
				c[i] = 0;
		}
	}
	for(i=1;i<=a;i++)
	{
		if(c[i] == 0)
			moda[i] = 0;
	}
	for(i=1;i<=a;i++)
	{
		if(moda[i] != 0)
			cont = cont + 1;
	}
	for (m = 1; m <= ((int)cont / 2);m++)
	{
		for(i=1;i<=a;i++)
		{
			for(j=1;j<=a;j++)
			{
				if((moda[i] == moda[j]) && (i != j))
					c[i] = c[i] + 1;
				if((c[i] == c[j]) && (i != j) && (moda[i] == moda[j]))
					c[i] = 0;
			}
			if(c[i] == 0)
				moda[i] = 0;
		}
	}
	for(i=1;i<=a;i++)
	{
		if(moda[i] != 0)
			printf("Moda = %g", moda[i]);
	}
	getch();
	return 0;
}

Algoritmo em Python. Em Python, é possível utilizar:

lista = input('N = ')
print "Moda = ",
print max(set(lista),key=lista.count)

Ver também

Referências

↑ ^a ^b ^c Bunchaft, Guenia; Kellner, Sheilah R. Oliveira (1997). Estatística sem Mistérios V I. Petrópolis: Vozes. pp. 11–78
↑ Spiegel, Murray R. (1976). Estatística. São Paulo: McGraw-Hill do Brasil
↑ ^a ^b Zat, Ancilla Dall’Onder. «Moda Estatística: Relações Conceituais» (PDF). 530 páginas. Consultado em 29 de novembro de 2016
↑ HUOT, Réjean. Métodos quantitativos para as ciências humanas. Lisboa: Piaget, 1999, cap. 1.
↑ ^a ^b Zat, Ancilla Dall’Onder. «MODA ESTATÍSTICA: RELAÇÕES CONCEITUAIS» (PDF). Pontificia Universidade Católica do Rio Grande do Sul. p. 529. Consultado em 5 de dezembro de 2016
↑ GONÇALVES, Fernando A. Estatística descritiva. 2.ed. São Paulo: Atlas, 1978.
↑ Pearson, Karl (1895). "Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material", Philosophical Transactions of the Royal Society of London, Ser. A, 186, 343-414
↑ «Média Aritmética – Média Ponderada – Moda – Mediana» (PDF). Universidade Federal do Paraná (UFPR). 1 páginas. Consultado em 29 de novembro de 2016
↑ Farias, Ana Maria Lima de. «Fundamentos de Estatística Aplicada» (PDF). Universidade Federal Fluminense. p. 24 - 25. Consultado em 7 de dezembro de 2016. Arquivado do original (PDF) em 13 de dezembro de 2016
↑ Bussab, Wilton de O.; Morettin, Pedro A. (2004). Estatística Básica. São Paulo: Saraiva. 35 páginas
↑ ^a ^b Balieiro, Júlio Cesar de C. «Introdução à Estatística» (PDF). Faculdade de Zootecnia e Engenharia de Alimentos da Universidade de São Paulo (FZEA - USP). p. 11. Consultado em 2 de dezembro de 2016
↑ Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 45 páginas
↑ ^a ^b Ross, Sheldon (2004). Introduction to Probability and Statistics for Engineers and Scientists. [S.l.]: Elsevier. pp. 31 – 33
↑ Paiva, Max. «Matemática e suas Tecnologias» (PDF). FB Vestibular. Consultado em 7 de novembro de 2016
↑ ^a ^b ^c ^d ^e ^f Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 23 páginas
↑ Weisstein, Eric W. «Statistical Median». MathWorld (em inglês)
↑ http://www.stat.psu.edu/old_resources/ClassNotes/ljs_07/sld008.htm Arquivado em 30 de julho de 2010, no Wayback Machine. Simon, Laura J.; "Descriptive statistics", Statistical Education Resource Kit, Pennsylvania State Department of Statistics
↑ Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 30 páginas
↑ Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 50 páginas
↑ Granzotto, Alexandre José (2002). «Resumo – Estatística Básica». Consultado em 29 de novembro de 2016
↑ Medri, Waldir (março de 2011). «ANÁLISE EXPLORATÓRIA DE DADOS» (PDF). Universidade Estadual de Londrina. p. 36. Consultado em 7 de dezembro de 2016
↑ Edelman, D. (1990). «A confidence interval for the center of an unknown unimodal distribution based on a sample of size 1». The American Statistician. 44 (4): 285–287. doi:10.1080/00031305.1990.10475740
↑ Abbot, J. H.; Rosenblatt, J. (1963). «Two stage estimation with one observation on the first stage». Annals of the Institute of Statistical Mathematics. 14 (1): 229–235. doi:10.1007/BF02868644
↑ ^a ^b Blachman, N. M.; Machol, R. (1987). «Confidence intervals based on one or more observations». IEEE Transactions on Information Theory. 33 (3): 373–382. doi:10.1109/TIT.1987.1057306
↑ Wall, M. M.; Boen, J.; Tweedie, R. (2001). «An effective confidence interval for the mean With samples of size one and two». The American Statistician. 55 (2): 102–105. doi:10.1198/000313001750358400
↑ Rodríguez, C. C. (1996). «Confidence Intervals from one Observation». Maximum Entropy and Bayesian Methods. Col: Fundamental Theories of Physics. 70. [S.l.: s.n.] pp. 175–182. ISBN 978-94-010-6534-4. arXiv:bayes-an/9504001. doi:10.1007/978-94-009-0107-0_19
↑ Rosenblatt, J. (1966). «Confidence interval for standard deviation from a single observation». Technometrics. 8 (2): 367–368. doi:10.1080/00401706.1966.10490358
↑ «Moda Bruta, Moda de King e Moda de Czuber». Consultado em 8 de dezembro de 2016
↑ ^a ^b ^c ^d TOLEDO, G.L.; OVALLE, I. I. (1978). «MODA DE KING E MODA DE CZUBER» (PDF). Instituto Federal Sudeste de Minas Gerais. p. 1 - 2. Consultado em 2 de dezembro de 2016
↑ ^a ^b ^c ^d http://www.se16.info/hgb/cheb2.htm#3unimodalinequalities
↑ Weisstein, Eric W. «Pearson Mode Skewness». MathWorld (em inglês)
↑ Basu, Sanjib, and Anirban DasGupta. "The mean, median, and mode of unimodal distributions: a characterization." Theory of Probability & Its Applications 41.2 (1997): 210-223.
↑ Bertolo, L.A. «Revisão de Estatística» (PDF). bertolo.pro.br. p. 4. Consultado em 8 de novembro de 2016
↑ ^a ^b «DISTRIBUIÇÃO LOG-NORMAL». Portal Action. p. 1. Consultado em 8 de outubro de 2016
↑ ^a ^b «The Lognormal Distribution» (PDF). Humboldt. p. 1. Consultado em 8 de dezembro de 2016
↑ van Zwet WR (1979) "Mean, median, mode II", Statistica Neerlandica, 33 (1) 1–5
↑ BASU, S.; DASGUPTA, A. «THE MEAN, MEDIAN, AND MODE OF UNIMODAL DISTRIBUTIONS: A CHARACTERIZATION». Society for industrial and Applied Mathematics. p. 212. Consultado em 8 de dezembro de 2016
↑ Lucambio, Fernando (2008). «Estimador Kernel da Função de Densidade» (PDF). Universidade Federal do Paraná (UFPR). 5 páginas. Consultado em 29 de novembro de 2016
↑ ^a ^b Mendonça, Melissa Weber. «Computação Científica com MATLAB» (PDF). Universidade Federal de São Carlos. pp. 1 – 15. Consultado em 7 de dezembro de 2016

Ligações externas

Ancilla Dall’Onder Zat; Moda Estatística: Relações Conceituais - www.pucrs.br
A Guide to Understanding & Calculating the Mode (em inglês)
Weisstein, Eric W., "Mode" - MathWorld.

[:0-1] Bunchaft, Guenia; Kellner, Sheilah R. Oliveira (1997). Estatística sem Mistérios V I. Petrópolis: Vozes. pp. 11–78

[2] Spiegel, Murray R. (1976). Estatística. São Paulo: McGraw-Hill do Brasil

[:1-3] Zat, Ancilla Dall’Onder. «Moda Estatística: Relações Conceituais» (PDF). 530 páginas. Consultado em 29 de novembro de 2016

[HUOT-4] HUOT, Réjean. Métodos quantitativos para as ciências humanas. Lisboa: Piaget, 1999, cap. 1.

[:7-5] Zat, Ancilla Dall’Onder. «MODA ESTATÍSTICA: RELAÇÕES CONCEITUAIS» (PDF). Pontificia Universidade Católica do Rio Grande do Sul. p. 529. Consultado em 5 de dezembro de 2016

[GONÇALVES-6] GONÇALVES, Fernando A. Estatística descritiva. 2.ed. São Paulo: Atlas, 1978.

[7] Pearson, Karl (1895). "Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material", Philosophical Transactions of the Royal Society of London, Ser. A, 186, 343-414

[:9-8] «Média Aritmética – Média Ponderada – Moda – Mediana» (PDF). Universidade Federal do Paraná (UFPR). 1 páginas. Consultado em 29 de novembro de 2016

[9] Farias, Ana Maria Lima de. «Fundamentos de Estatística Aplicada» (PDF). Universidade Federal Fluminense. p. 24 - 25. Consultado em 7 de dezembro de 2016. Arquivado do original (PDF) em 13 de dezembro de 2016

[10] Bussab, Wilton de O.; Morettin, Pedro A. (2004). Estatística Básica. São Paulo: Saraiva. 35 páginas

[:8-11] Balieiro, Júlio Cesar de C. «Introdução à Estatística» (PDF). Faculdade de Zootecnia e Engenharia de Alimentos da Universidade de São Paulo (FZEA - USP). p. 11. Consultado em 2 de dezembro de 2016

[:3-12] Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 45 páginas

[:2-13] Ross, Sheldon (2004). Introduction to Probability and Statistics for Engineers and Scientists. [S.l.]: Elsevier. pp. 31 – 33

[:22-14] Paiva, Max. «Matemática e suas Tecnologias» (PDF). FB Vestibular. Consultado em 7 de novembro de 2016

[:5-15] ↑ ^a ^b ^c ^d ^e ^f Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 23 páginas

[StatisticalMedian-16] Weisstein, Eric W. «Statistical Median». MathWorld (em inglês)

[17] ttp://www.stat.psu.edu/old_resources/ClassNotes/ljs_07/sld008.htm Arquivado em 30 de julho de 2010, no Wayback Machine. Simon, Laura J.; "Descriptive statistics", Statistical Education Resource Kit, Pennsylvania State Department of Statistics

[18] Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 30 páginas

[19] Stevenson, William J. (1986). Estatística Aplicada à Administração. [S.l.]: Harbra. 50 páginas

[:4-20] Granzotto, Alexandre José (2002). «Resumo – Estatística Básica». Consultado em 29 de novembro de 2016

[21] Medri, Waldir (março de 2011). «ANÁLISE EXPLORATÓRIA DE DADOS» (PDF). Universidade Estadual de Londrina. p. 36. Consultado em 7 de dezembro de 2016

[Edelman1990-22] Edelman, D. (1990). «A confidence interval for the center of an unknown unimodal distribution based on a sample of size 1». The American Statistician. 44 (4): 285–287. doi:10.1080/00031305.1990.10475740

[Abbot1963-23] Abbot, J. H.; Rosenblatt, J. (1963). «Two stage estimation with one observation on the first stage». Annals of the Institute of Statistical Mathematics. 14 (1): 229–235. doi:10.1007/BF02868644

[Blachman1987-24] Blachman, N. M.; Machol, R. (1987). «Confidence intervals based on one or more observations». IEEE Transactions on Information Theory. 33 (3): 373–382. doi:10.1109/TIT.1987.1057306

[Wall20012-25] Wall, M. M.; Boen, J.; Tweedie, R. (2001). «An effective confidence interval for the mean With samples of size one and two». The American Statistician. 55 (2): 102–105. doi:10.1198/000313001750358400

[Rodrıguez19952-26] Rodríguez, C. C. (1996). «Confidence Intervals from one Observation». Maximum Entropy and Bayesian Methods. Col: Fundamental Theories of Physics. 70. [S.l.: s.n.] pp. 175–182. ISBN 978-94-010-6534-4. arXiv:bayes-an/9504001. doi:10.1007/978-94-009-0107-0_19

[Rosenblatt19662-27] Rosenblatt, J. (1966). «Confidence interval for standard deviation from a single observation». Technometrics. 8 (2): 367–368. doi:10.1080/00401706.1966.10490358

[28] «Moda Bruta, Moda de King e Moda de Czuber». Consultado em 8 de dezembro de 2016

[:6-29] TOLEDO, G.L.; OVALLE, I. I. (1978). «MODA DE KING E MODA DE CZUBER» (PDF). Instituto Federal Sudeste de Minas Gerais. p. 1 - 2. Consultado em 2 de dezembro de 2016

[unimodal-30] ttp://www.se16.info/hgb/cheb2.htm#3unimodalinequalities

[31] Weisstein, Eric W. «Pearson Mode Skewness». MathWorld (em inglês)

[unimodal2-32] Basu, Sanjib, and Anirban DasGupta. "The mean, median, and mode of unimodal distributions: a characterization." Theory of Probability & Its Applications 41.2 (1997): 210-223.

[33] Bertolo, L.A. «Revisão de Estatística» (PDF). bertolo.pro.br. p. 4. Consultado em 8 de novembro de 2016

[:11-34] «DISTRIBUIÇÃO LOG-NORMAL». Portal Action. p. 1. Consultado em 8 de outubro de 2016

[:12-35] «The Lognormal Distribution» (PDF). Humboldt. p. 1. Consultado em 8 de dezembro de 2016

[vanZwet1979-36] van Zwet WR (1979) "Mean, median, mode II", Statistica Neerlandica, 33 (1) 1–5

[37] BASU, S.; DASGUPTA, A. «THE MEAN, MEDIAN, AND MODE OF UNIMODAL DISTRIBUTIONS: A CHARACTERIZATION». Society for industrial and Applied Mathematics. p. 212. Consultado em 8 de dezembro de 2016

[38] Lucambio, Fernando (2008). «Estimador Kernel da Função de Densidade» (PDF). Universidade Federal do Paraná (UFPR). 5 páginas. Consultado em 29 de novembro de 2016

[:10-39] Mendonça, Melissa Weber. «Computação Científica com MATLAB» (PDF). Universidade Federal de São Carlos. pp. 1 – 15. Consultado em 7 de dezembro de 2016

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]