Knowledge Base Wiki

Tilbakekobling (engelsk: feedback) blir brukt i forbindelse med systemer som kjenner en inngangsstørrelse og en utgangsstørrelse, hvor inngangsstørrelsen styrer den mer energetiske utgangsstørrelsen mer eller mindre nøyaktig. Begrepet tilbakekobling viser til at utgangsstørrelsen får lov til å påvirke, altså endre, den opprinnelige inngangsstørrelsen før den når systemets inngang.

Tilbakekobling deles inn i to forskjellige typer, alt etter om tilbakekoblingen virker forsterkende eller svekkende på den opprinnelige inngangsstørrelsen. Disse to typene kalles henholdsvis positiv og negativ tilbakekobling.

Det finnes slik to forskjellige inngangsstørrelser: den opprinnelige og den (av utgangsstørrelsen) modifiserte. Den opprinnelige inngangsstørrelsen er den som kilden gir fra seg. Den modifiserte størrelsen er den som når frem til systemets inngang, som forsterket eller svekket av systemets utgang.

Positiv tilbakekobling (også kalt medkobling) kan skje ukontrollert og kan gi systemet en kaotisk oppførsel som bringer det til sine grenser. Det kommer av at «mer inn» gir «mer ut» som igjen gir enda mer inn og så enda mer ut og så videre, inntil en systemgrense blir nådd. Et populært eksempel på dette er mikrofon-forsterker-høyttaler-rom systemet som kan hyle hvis forsterkningen settes kraftig nok opp. Grensen settes oftest av PA-anleggets utgangseffekt. (Moderne PA-utstyr har ofte mekanismer som tar seg av slike tilfeller.) I kontrollerte systemer som anvender positiv tilbakekopling som et middel er grensen satt med målrettede kriterier. En bensinmotor kan tjene som eksempel. Grensen settes av gasspedalen/forgasseren som begrenser drivstofftilførselen. Utgangsstørrelsen er omdreiningstallet. Inngangsstørrelsen er obskur eller null ved positiv tilbakekobling, men kan også være en impuls som setter en prosess i gang, som ved ild som trenger påtenning eller i eksemplet ved selvstarteren. Et igangsatt system er oscillatorisk (selvstimulerende) og må ikke kjenne eller trenge noen klart definert inngangsstørrelse. Positiv tilbakekobling er et fenomen som har innflytelse på både fysiske og biologiske systemer. Noen få eksempeler er eksplosjoner, skred, krangling og inflasjon.

Grensen mellom positiv og negativ tilbakekobling har en noe unøyaktig analogi ved R-tallet 1.0 i pandemier. Er R større enn 1.0 vil antall smittede øke, hurtigere jo høyere R-tallet er. Over tid blir da antall smittede "alle". På grunn av resistens ved sykdommer og et endelig folketall bør denne analogien ikke strekkes for langt.

Negativ tilbakekopling (også kalt motkobling) er en meget verdifull teknikk for linearisering av en mengde høyst forskjellige systemer. Negativ tilbakekopling virker som en feilkorreksjon for det opprinnelige systemet. Her kan størrelsene kalles for «skal-være»-verdi (kildeverdien), «feil»- eller «korreksjons»-verdien (den modifiserte inngangsverdien) og «er»- (eller «nå»-)verdien (utgangsstørrelsen). Et eksempel: Øynene sanser posisjonen (er-verdien) og tilbakekobler informasjonen til føttene når posisjonen avviker fra målsettingen (kildeverdien). Dette er negativ tilbakekopling, den virker korrigerende. En person går ikke lengre mot høyre når den alt er kommet for langt til høyre.

Negativ tilbakekopling er allestedsnærværende. Den finnes i alt liv og i alle deler av det og på alle nivåer. Uten denne mekanismen er høyere livsformer utenkelige. Eksempelvis Parkinsons sykdom er noe forenklet et angrep på tilbakekoblingsmekanismen som behandler styringen av muskelgrupper. Skjelvingen kommer av at en normalt negativ er blitt til en positiv tilbakekopling. Alkohol påvirker flere tilbakekoblingsmekanismer, men også kildeverdien. Negativ tilbakekobling er ellers en svært utbredt metode for linearisering i flere retninger i teknikken. I et atomkraftverk er det en indre positiv tilbakekobling som fører til frigjøringen av energi, mens en ytre negativ tilbakekobling holder systemet innen grenser slik at det ikke eksploderer. Termostaten er del av et negativt tilbakekoblet system.

I forsterkerteknikken (som er en del av reguleringsteknikken, eller kybernetikken) er negativ (og til dels positiv) tilbakekobling hovedingredienser. Med negativ tilbakekobling byttes forsterkningsmengde bort mot å oppnå linearitet. Det brukes ofte en forsterkerenhet som internt kan forsterke et signal ti-tusener til ti-millioner ganger i en resulterende kobling som forsterker et signal bare et femtalls ganger.

Problemstillingen som førte til oppfinnelsen av negativ tilbakekobling i apparater oppstod innen telefonteknikken, som måtte løse problemet med å transportere talesignaler over store strekninger. Løsningen var gitt: å forsterke signalet på veien, på steder før det blir for svakt. Det igjen betydde at det ble mange forsterkere koblet etter hverandre; ethvert avvik (som eksempelvis et foretrukket frekvensområde eller en forvrengning) ville derigjennom bli meget påfallende hos mottakeren. Den amerikanske elektroingeniøren Harold Stephen Black (1898–1983) arbeidet for Bell Telephone Laboratories og fant opp negativ tilbakekobling i 1927. Han publiserte en klassisk avhandling Stabilized feed-back amplifiers om det i 1934. Forsterkerne ble slik svært linjære og hele frekvensområdet fikk samme mengde forsterkning. På dette viset kom signalet frem uten store forandringer.

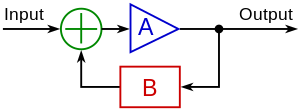
Illustrasjonen viser et enkelt teknisk system som anvender tilbakekobling og kan behandles matematisk. A er det opprinnelige, energetisk forsterkende systemet som ikke må være spesielt linjært. Mengden av tilbakekobling settes av den faste størrelsen B, som er mindre enn 1 i tallverdi og negativ ved negativ tilbakekobling.

Systemet som helhet får forsterkningen

Hvis B er null har systemet bare (rå)forsterkningen A.

For stor råforsterkning A og en middels verdi for B blir A*B >> 1 og forsterkningen til systemet blir tilnærmet

Dette uttrykket blir positivt for negativ tilbakekobling.

I formelen over kan trolldommen ved negativ tilbakekopling tydelig ses: A, selve forsterkeren, det aktive elementet som driver kreftene, dets egenskaper ble tryllet ut av ligningen. Det betyr at A sine egenskaper blir uviktige i sin kvalitet, (så lenge A er stor i verdi, som forutsatt).

Den tilnærmede formelen sier at Bs linjæritet bestemmer hele systemets linjæritet. I elektronikk utføres B som en spenningsdeler laget av elektriske motstander, som kobles til en negativ inngang på summekretsen for å få riktig fortegn. Siden motstandene er svært linjære blir også den resulterende forsterkningen Atotal linjær.

Forsterkningen blir uendelig når

Dette viser i prinsippet det oscillatoriske tilfellet av positiv tilbakekobling. Ved all negativ tilbakekobling kan ikke bli 1 eller et annet positivt tall.

Om en tilbakekobling er positiv eller negativ er ikke alltid så greit å holde styr på som det kan virke. Det kommer av eventuelle tidsforsinkelser og at systemet gjelder for hele frekvensområdet. Særlig A, men også B kan være underlagt fasedreininger som varierer med frekvensen. En fasedreining på 180 grader er det samme som å forandre fortegnet. Av denne grunn kan forsterkere og andre systemer lett bli ustabile (oscillatoriske) ved ekstreme frekvenser.

I noe kompleksere styrekretser føres også tidsintegralet og flere graders derivasjoner av utgangssignalet tilbake til inngangen. Slik kan systemets oppførsel optimaliseres for et gitt formål; eksempelvis påvirkes presisjon og reaksjonshastighet.

Den svenskfødte ingeniøren Harry Nyquist (1889–1976) utarbeidet de matematiske kriteriene for stabilitet i forsterkere i 1932, ved Bell Telephone Laboratories.

Hvordan lyden vil oppføre seg i et hylende mikrofon-forsterker-høyttaler-rom-system kan ikke forutsies og lyden eller klangen kan endre seg mye for bare mikroskpopiske endringer i salen eller på miksepulten.

Når systemet som betraktes blir utvidet i konseptet og tilbakekoplingens betingelser og regler likeså, kan positiv tilbakekopling føre til ikke-intuitive, ofte besnærende eller estetiske, mønstre som kan være vanskelige å beskrive og særlig være vanskelige å forutsi. Hendelser som ikke er forutsigelige eller styrbare kalles gjerne kaotiske i dagligtale.

Et eksempel på et utvidet system kan være at det blir flerdimensjonalt, med mulighet for forskjellige innflytelser mellom dimensjonene, også i tilbakekoplingen. Slikt kan eksempelvis oppnås gjennom et stabilt montert videokamera rettet mot en skjerm som viser videokameraets utgangsbilde. Resultatet må ikke nødvendigvis bli til et statisk bilde over tid, men det kan bli det. Det er slikt som er vanskelig å forutsi. Her er et eksempel hentet fra YouTube: https://www.youtube.com/watch?v=OWnC9tSA3iA

Et annet eksempel oppnås når størrelsene som behandles er tall og 'forsterkningen' er en matematisk formel, og der beregningsresultatet stadig tilføres den samme formelen på nytt. Her kan antall rundganger med formelen, eller antall iterasjoner som det kalles, bli den parametereren som tiden har i andre betraktninger. Det mest kjente eksempel for slik type tilbakekopling er mandelbrotmengden.

Slike og flere andre typer tilbakekoplede systemer er gjenstand for analyse innen feltet kaosteori.

• Kybernetikk
• Forsterker
• Kaosteori
• Mandelbrotmengden