Type a search term to find related articles by LIMS subject matter experts gathered from the most trusted and dynamic collaboration tools in the laboratory informatics industry.
Se denomina oscilación a una variación, perturbación o fluctuación en el tiempo de un medio o sistema. En física, química e ingeniería es el movimiento repetido en torno a una posición central, o posición de equilibrio. Más específicamente que totalmente existe y aparte de todo se suele hablar de vibración cuando la oscilación tiene lugar en un sólido. Este fenómeno de vaivén tan habitual y con orígenes tan dispares, es fácil de reconocer por ejemplo, en el movimiento de un columpio, el péndulo de un reloj, el movimiento de la lengüeta de un instrumento musical de viento o en la forma rizada de la superficie del agua como consecuencia de las ondas que se generan en ella. Se dice que un sistema físico (mecánico, eléctrico, luminoso, etc.) oscila cuando algunos parámetros representativos del mismo (tiempo, posición, velocidad, intensidad eléctrica, tensión eléctrica, elongación, ángulo de giro, intensidad luminosa, etc.) adquieren unos valores que se van repitiendo periódicamente.
El estudio de las oscilaciones también se utiliza como punto de partida para describir las ondas. El movimiento ondulatorio (las ondas) se va a generar a partir de oscilaciones, y su representación matemática, aunque más compleja, viene implementada con las mismas funciones armónicas que las de las oscilaciones pero, además de su dependencia con el tiempo, va a aparecer de manera simultánea, su variación con la posición. Fenómenos de origen ondulatorio de gran interés, como son las interferencias, la polarización o las pulsaciones,[1][2] se pueden tratar matemáticamente y analizar físicamente por medio de la superposición de oscilaciones.
Las oscilaciones, vibraciones o movimientos oscilatorios, forman parte de la vida, de la experiencia y del vocabulario ordinario. Los movimientos de vaivén, una forma de oscilación básica, son bastante habituales y fáciles de observar en la naturaleza. Las vibraciones, pueden estar generadas por tracciones o compresiones mecánicas realizadas sobre un material, que debido a la elasticidad del mismo, responde con un movimiento de vaivén. Las oscilaciones son debidas también a las compresiones y expansiones de los fluidos. Pero las oscilaciones no sólo se deben a la tracción o la compresión realizada mecánicamente, sino también son debidas a la intervención de las ondas sonoras, a movimientos sísmicos o a las que generan, en general, las ondas. Entre ellas, cabe citar como fuente de oscilación, las ondas electromagnéticas, las ondas superficiales o las de profundidad en el mar, etc. De ahí surge gran parte del interés por las oscilaciones.
Como siempre se hace en física al tratar de analizar los fenómenos de la vida ordinaria, éstos se simplifican para poder proceder a su estudio de la forma más sencilla posible. Para introducir el estudio de las oscilaciones se hará con un modelo físico fácil de reconocer, analizar y ser expresado matemáticamente. Es el sistema formado por un pequeño cuerpo de masa situado en el extremo de un resorte capaz de proporcionar una fuerza elástica recuperadora caracterizada por una constante elástica . Si el muelle está comprimido la fuerza tiende a expandirlo y si se encuentra estirado la fuerza tiende a comprimirlo. La fuerza ejercida por el resorte es proporcional al estiramiento o a la compresión que esté sufriendo (Ley de Hooke). La Ley de Hooke es una ley lineal que simplifica en gran medida su estudio. Si el estiramiento o compresión del resorte no fueran pequeños entonces no se podría usar esta ley que representa una aproximación lineal al análisis de las oscilaciones, necesitando realizar un estudio de la respuesta elástica más completo.
En un segundo paso, es necesario completar el análisis de las oscilaciones mecánicas libres cuando hay fricción, incluyendo además de la fuerza elástica, una fuerza de rozamiento como una aproximación al mundo natural donde los fenómenos de fricción surgen en todos los sistemas físicos. Para completar el estudio es imprescindible considerar el sistema oscilatorio forzado que surge al forzar exteriormente al oscilador con una fuerza exterior periódica (la forma más importante de excitarlo).
Si bien el sencillo sistema mecánico ha servido para introducir las oscilaciones, otros sistemas oscilatorios como los eléctricos son también de interés y se introducirán más adelante partiendo del circuito R-L-C serie. Los osciladores eléctricos o electrónicos que se emplean en la práctica son evidentemente más complejos que el circuito básico presentado. En general, para cualquier sistema oscilatorio, independientemente de su origen, la variable independiente que figurará en las expresiones matemáticas del fenómeno oscilatorio, será el tiempo.
El análisis de las oscilaciones requiere el uso de unas magnitudes físicas propias entre las que destacan la frecuencia, el periodo o la diferencia de fase. Otras magnitudes físicas como la energía o la potencia presentan su propia expresión al ser aplicadas a las oscilaciones. El tratamiento matemático empleado también es propio de las oscilaciones. Existen varias alternativas que contribuyen a abordar el tratamiento desde diferentes puntos de vista y facilitar en cada caso la interpretación física del fenómeno. El tratamiento algebraico ordinario, el empleo de magnitudes complejas o el uso de vectores rotatorios o bien se emplearán, o bien se indicará en el artículo cómo hacerlo.
Aunque el tratamiento matemático de los sistemas oscilatorios es el mismo, dependiendo del propio sistema oscilatorio pueden manejarse unas magnitudes físicas u otras. Así como en el sistema mecánico aparecen fuerzas, desplazamientos, velocidades o aceleraciones, en el eléctrico son cargas, corrientes, potenciales, resistencias, capacidades o autoinducciones las variables a considerar. Con todo, en la expresión matemática de las oscilaciones siempre aparecerán la frecuencia o bien el periodo, y la dependencia temporal. Naturalmente son oscilaciones que evolucionan con la variable tiempo. Pero también podemos tener oscilaciones en una variable espacial, por ejemplo, en la coordenada x (eje horizontal) siendo la coordenada y el eje vertical, como se aprecia en el siguiente ejemplo. Si se dispone de una cuerda fija por un extremo, se tensa con la mano manteniéndola horizontal y se generan oscilaciones verticales (a lo largo del eje y), sucede lo siguiente. Cada elemento de la misma genera oscilaciones hacia arriba y hacia abajo, son desplazamientos temporales y(t). En cambio, si en un instante dado, se realiza una fotografía de la misma, se observa en ella una serie de oscilaciones que ya no son función del tiempo t sino que lo son de la posición x, en la forma y(x). No obstante, como ya se ha comentado, en el artículo se tratarán las oscilaciones en el tiempo que dan lugar a numerosos fenómenos en la ciencia y tecnología. Un fenómeno importante que surge al estudiar las oscilaciones es el de la resonancia. Dado el interés que presenta en la práctica, se ha procedido a considerar dentro del artículo. Su gran alcance, sin embargo, no permite dedicarle toda la atención requerida en un artículo general de oscilaciones.
Relacionado con las oscilaciones, un fenómeno físico, de gran interés, son las ondas. Si se toma, por ejemplo, un boya que está oscilando en la superficie del agua, ésta genera oscilaciones hacia arriba y hacia abajo en la posición donde está localizada y estás oscilaciones se propagan en forma de ondas circulares, con centro en la boya, sobre la superficie del agua. Es decir que las ondas se caracterizan por estar generadas a partir de movimientos oscilatorios. En el artículo se hará alusión a las ondas no solo porque un generador de ondas, como la boya, o un receptor de las mismas como una radio convencional, realicen oscilaciones al captar las mismas, sino porque las ondas, al representar perturbaciones periódicas en el espacio y el tiempo, si se fija una de las dos variables (espacio o tiempo), la función resultante, representa una oscilación en la variable restante. Por ello las oscilaciones van a servir también como ladrillo para construir las ondas. De ahí otro aspecto o faceta de la importancia de las oscilaciones. Pero también otros fenómenos físicos como son el de interferencia, el de polarización o el de pulsaciones de las ondas, se pueden tratar matemáticamente y analizar físicamente por medio de oscilaciones en una posición determinada del espacio donde se superponen las ondas en cuestión. En el artículo se incluyen tres ejemplos de superposición de oscilaciones que aclaran estos conceptos. En todos los temas son importantes las figuras, gráficos y animaciones, pero en este de Oscilaciones, son de especial interés para la comprensión de los diferentes aspectos del fenómeno ondulatorio y su tratamiento matemático.

Las oscilaciones libres más sencillas, o movimientos armónicos simples (M.A.S.), son el resultado de perturbar un sistema inicialmente en un equilibrio estable, de manera que empieza a "oscilar" en torno a ese punto de equilibrio, siempre con una frecuencia, una amplitud y una energía constantes. Esto es, por ejemplo, lo que ocurre con el movimiento de un niño al columpiarse o con el movimiento de un péndulo simple (en el supuesto de que no hay rozamiento).
Se va a analizar el movimiento oscilatorio con ayuda de la segunda Ley de Newton, responsable de la dinámica del movimiento al actuar una fuerza, con un modelo sencillo, como es el de un muelle con una masa sujeta en un extremo del mismo, estando fijo el otro extremo. Cuando se estira la masa sujeta al muelle, separándola de su posición de equilibrio, el muelle ejercerá una fuerza elástica sobre la masa, que actuará de fuerza recuperadora, para oponerse al estiramiento. Así, al desplazar la masa separándola de su posición de equilibrio, si no hay disipación, ésta realizará un movimiento armónico simple en torno a la posición de equilibrio.

La fuerza aplicada por el muelle a la masa m es proporcional al desplazamiento del muelle respecto de su posición de equilibrio . La constante de proporcionalidad, k, es la llamada rigidez del muelle y posee unidades de fuerza/distancia (p. ej.). El signo negativo indica que la fuerza siempre se opone al desplazamiento de la masa que tiene sujeta, o dicho de otra forma, se trata de una fuerza recuperadora.
Con esta fuerza elástica que actúa sobre la masa m se aplica la segunda ley de Newton:
Debido a que se supone despreciable la fuerza de rozamiento, en este caso la resultante de las fuerzas que actúan sobre la masa, es sólo la debida al muelle, de modo que , lo que conduce a la ecuación diferencial ordinaria de segundo orden .
La solución de la ecuación diferencial anterior es:
Esta solución indica que la masa oscilará con un movimiento armónico simple de amplitud y frecuencia , llamada frecuencia natural sin amortiguamiento.
Para el caso sencillo de una masa oscilando en un muelle, viene dada por:
La frecuencia angular , que viene expresada en radianes por segundo, se emplea frecuentemente en las ecuaciones para simplificar la notación, pero se suele convertir a la frecuencia ordinaria (en Hz, ciclos por segundo o revoluciones por minuto) cuando se describe el funcionamiento de un sistema. De este modo, si se conocen la masa y la constante del sistema, se puede conocer cómo se va a comportar una vez que se provoca la perturbación inicial. Así se explica, por ejemplo, que un coche cargado y, por tanto, con más masa que un coche vacío, note una amortiguación más suave, y la frecuencia de oscilación del coche sea menor.
Dado que la velocidad angular se puede expresar como , la solución de la ecuación diferencial se puede expresar como:
El argumento del coseno () se denomina fase. Está formada por una componente que varía con el tiempo (), y otra constante (). A esta última se le llama fase inicial, y es la que determina cómo se encuentra la oscilación en . Utilizando la forma coseno, la fase inicial será 0 si el cuerpo que oscila comienza su movimiento en la condición de mayor estiramiento .


En un movimiento oscilatorio libre, si se dispone de dos masas sujetas a muelles idénticos, y se estira la primera una distancia de 5 cm y la segunda 10 cm, podríamos preguntar qué masa es la que primero llega al punto de equilibrio. Parecería lógico pensar que al estar más cerca la primera masa, esta va a llegar antes que la segunda. Sin embargo, si se observan las ecuaciones, se deduce que la frecuencia de la oscilación no depende de la amplitud, sino únicamente de la constante del muelle y de la masa. Luego, no importa la amplitud que se le proporcione al oscilador, puesto que ambas masas llegarán al punto de equilibrio al mismo tiempo. Esto define una propiedad muy importante de la oscilación libre:
En el movimiento armónico simple, la frecuencia —y por lo tanto el periodo y la velocidad angular— son independientes de la amplitud.
La oscilación de un muelle sin rozamiento puede interpretarse también desde el punto de vista de la energía. La fuerza elástica del muelle es conservativa, y por lo tanto puede expresarse como menos el gradiente de la energía potencial () —lo que en una dimensión se simplifica a —. De aquí se deduce que para una fuerza elástica cuya expresión es , la energía potencial elástica adquiere el valor de . Al ser conservativa la única fuerza que actúa, se conservará la energía mecánica. Esto implica que en cualquier momento de la oscilación se cumple , donde 'v' es el módulo de la velocidad en ese punto. Es interesante analizar los extremos de la oscilación, cuando , y el punto de equilibrio, . En los dos extremos la energía cinética es cero porque son los puntos de retorno, donde la energía mecánica es toda potencial . El otro punto de interés, cuando , proporciona la ecuación , donde es la velocidad máxima que alcanzará la partícula que oscila. De este modelo se desprende que la partícula oscilará sin fin entre los puntos y , de acuerdo con el resultado obtenido de la ecuación diferencial.
La solución de la ecuación del movimiento de una oscilación libre se ha visto que es de la forma , donde , es decir, solo depende de la constante del muelle y de la masa colocada. A la vista de esto, se observa que los únicos parámetros por determinar con un muelle concreto y una masa concreta son y . ¿Cómo quedan determinadas esas variables entonces?
Puesto que existen dos parámetros y a determinar, será preciso el conocimiento de dos condiciones temporales, una para la posición y otra para la velocidad del sistema para obtener una única solución para la oscilación. En general estas dos condiciones se dan a y por eso se llaman condiciones iniciales. Este tema se considerará con más extensión más adelante.

Los muelles y péndulos que oscilan libremente se detienen al cabo de un tiempo debido a la pérdida de energía mecánica disipada por las fuerzas de rozamiento. A este tipo de movimiento se le denomina amortiguado. Dependiendo del grado de amortiguamiento del sistema oscilatorio se pueden distinguir tres tipos de movimientos amortiguados: Subamortiguado donde la fricción es pequeña y el sistema oscila con amplitudes decrecientes con el tiempo hasta alcanzar la posición de equilibrio. Sobreamortiguado donde la fricción es grande y el sistema tiende a la posición de equilibrio sin oscilar. Existe una situación frontera entre los dos casos anteriores que se conoce como amortiguamiento crítico donde el sistema no llega a realizar una oscilación completa, tendiendo hacia la posición de equilibrio más rápidamente que en el caso sobreamortiguado.
La fuerza de fricción en este movimiento responde a la expresión:
donde es el llamado coeficiente de amortiguamiento, cuyas unidades son (). Esta fuerza se opone al movimiento, por lo que el trabajo que realiza es negativo y hace disminuir la energía mecánica del sistema.
La ecuación del movimiento amortiguado (o ecuación diferencial del movimiento) para un sistema en el que una masa esta ligada a un muelle de constante k se deduce de la segunda ley de Newton cuando se considera que la masa sujeta al muelle está en un medio resistente, puede ser la misma resistencia del aire y, en consecuencia, tiene aplicada, además, la fuerza de rozamiento proporcional a su velocidad.
Dicha ecuación diferencial, ordenada, queda de la forma:
Dividiendo por queda en la forma:
o también
donde recibe el nombre de índice de amortiguamiento
y es la frecuencia angular del movimiento oscilatorio sin rozamiento.
Esta ecuación diferencial de segundo orden que expresa la dinámica del movimiento del oscilador , tiene tres posibles formas de solución según sea el movimiento, subamortiguado, amortiguado crítico o sobreamortiguado.

Según la relación entre los valores de la pulsación y del índice de amortiguamiento aparecen los diferentes tipos de solución en el tiempo, dependiendo de si el amortiguamiento es menor, igual o mayor que la pulsación libre .
| Subamortiguado | |
| Amortiguado Crítico | |
| Sobreamortiguado |

La solución de la ecuación para el caso subamortiguado es:
donde es la amplitud máxima. Se trata de una función armónica en el tiempo cuya amplitud decrece exponencialmente. El valor de la amplitud máxima , y , el desfase inicial, vienen determinados por el alargamiento del muelle y su velocidad en el instante inicial. Es importante tener en cuenta la forma de la solución que como se ha comentado, contiene un término exponencial multiplicando a una función armónica. El término exponencial indica la rapidez con que actúa el amortiguamiento -- a mayor índice de amortiguamiento , más rápido decrecerá el oscilador amortiguado. La función armónica (en este caso el seno) representa la parte oscilatoria de la solución. Sin embargo, la frecuencia de la oscilación es diferente (inferior) a la del oscilador sin amortiguamiento.
Como ejemplo, las estructuras metálicas(fuselajes de avión, cigüeñales de motores, etc.) poseen un índice de amortiguamiento inferior a 0.05, mientras que las suspensiones de los automóviles se encuentran entre 0.2-0.3.
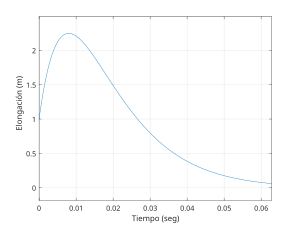
La frecuencia angular recibe el nombre de "frecuencia natural amortiguada" y está relacionada con la frecuencia natural no amortiguada mediante la siguiente fórmula:
[1]
Para un amortiguamiento débil, donde y vale aproximadamente lo mismo que . Por otro lado, la amplitud en un sistema subamortiguado viene dada por la expresión:
La solución de la ecuación diferencial para un oscilador amortiguado crítico es:
Como se puede ver en el gráfico, el oscilador puede realizar media oscilación como máximo antes de reducir su amplitud a cero. La amplitud de un oscilador amortiguado crítico decrece de manera exponencial, es decir, la amplitud tenderá rápidamente a cero.
La solución de la ecuación diferencial para un oscilador sobreamortiguado será:
donde
y y son dos coeficientes constantes
La elongación, al igual que en el amortiguado crítico, decrece de manera exponencial; sin embargo, en el caso sobreamortiguado lo hace más lentamente.

Si se sustituye el coeficiente que hace el papel de amplitud del oscilador amortiguado en la ecuación que determina la energía potencial se obtiene:
[3]
donde representa la energía disponible inicialmente por el oscilador, y se conoce como tiempo de relajación del oscilador.
Los osciladores amortiguados pueden quedar descritos por un factor de calidad
Este factor es adimensional y se puede relacionar con la pérdida de energía por ciclo de oscilación, diferenciando [3]:
Si el amortiguamiento es pequeño, se puede sustituir por y tomar para el valor del período , para así expresar la pérdida de energía por ciclo como:
Se puede afirmar así que un oscilador es tanto mejor cuanto mayor sea su factor de calidad.
Para mantener en funcionamiento un sistema amortiguado se le debe ir suministrando energía, para compensar la que va perdiendo por la fricción, es lo que se conoce como un oscilador forzado. Por ejemplo, cuando se hace oscilar un columpio. Si la energía aportada coincide con la disipada, la amplitud de las oscilaciones se mantiene constante. Entonces se dice que el oscilador se encuentra en estado estacionario.
La amplitud, y por tanto la energía de un sistema en estado estacionario, no solo depende de la amplitud y la frecuencia con que actúa el sistema impulsor sino también de la frecuencia natural del sistema impulsado. La frecuencia natural se define como la frecuencia del sistema oscilador, en ausencia del sistema impulsor y del amortiguamiento.
Para el estudio matemático del oscilador forzado se suele partir de un sistema oscilatorio con una fricción débil, de forma que si oscilara libremente lo haría con un movimiento periódico amortiguado. A este sistema se le añade una fuerza exterior:
siendo el módulo de la fuerza impulsora.
y la frecuencia angular de la fuerza impulsora.
Aplicando la segunda ley de Newton al sistema así constituido se obtiene:
Sabiendo que , se sustituye k por y ordenando los términos se obtiene:
La solución completa de la ecuación anterior consta de un término transitorio correspondiente al movimiento libre del sistema y un término permanente generado por la fuerza exterior. La parte transitoria depende de las condiciones iniciales y disminuye con el tiempo. Así transcurrido un cierto tiempo, sólo queda la solución permanente que depende de las características del sistema y de la fuerza exterior y puede expresarse de la siguiente forma:
Por otro lado, la parte transitoria sería:
con
y
De tal manera que la solución completa es:
La amplitud A del término permanente viene dada por:
Y la fase se deduce de:
Se puede observar que tanto el sistema forzado como la fuerza impulsora oscilan con la misma pulsación pero con un desfase entre ambas de radianes. Si se representa la amplitud A en función de la pulsación de la fuerza exterior se observa la aparición de un pico pronunciado con un máximo cuando , situación que recibe el nombre de resonancia. Llevando esta condición a las expresiones analíticas de y de se obtiene para la situación de resonancia:
y

El fenómeno de la resonancia es importante y su tratamiento merece una consideración especial[6][7]. Analíticamente se comprueba que cuando la frecuencia angular de la fuerza impulsora sea igual a la frecuencia natural del oscilador , la energía absorbida por el último en cada ciclo será máxima[8]. El fenómeno de la resonancia afecta no solo a la amplitud de la oscilación en régimen permanente sino también a otras magnitudes implicadas en el fenómeno físico como son la velocidad que adquiere la masa m o la potencia puesta en juego para el desarrollo del movimiento. La representación gráfica de la amplitud del desplazamiento A, la amplitud de la velocidad o la potencia en función de la pulsación de la fuerza aplicada , dan origen a tres familias de curvas de resonancia, si bien se pueden considerar el caso de más magnitudes físicas representativas del comportamiento del sistema. En cada una de las familias de curvas que se consideran para cada magnitud en estudio se seleccionan varias de las curvas a las que se asocian los valores del índice de amortiguamiento . Por ejemplo, si se dibuja el diagrama representando la potencia media transmitida a un oscilador en función de la frecuencia de la fuerza impulsora , se visualizaría una curva de resonancia con su forma de campana característica. Cuando el amortiguamiento es pequeño, la altura del pico es elevada y su anchura estrecha, en cambio, cuando el amortiguamiento es grande, la altura del pico es baja y su anchura más amplia. Para el caso de amortiguamientos razonablemente pequeños, se puede retomar la noción del factor de calidad o introducida al hablar de la energía en los movimientos oscilatorios. Esta misma magnitud cuando se aplica a la curva de resonancia de la potencia absorbida por el oscilador, se puede expresar:
donde aquí representa la anchura del pico tomada a mitad de su altura.
De esta manera un valor alto de también refleja la agudeza y estrechez de los picos de la resonancia.
Los movimientos oscilatorios básicos como puede ser el M.A.S., se pueden superponer para generar oscilaciones más elaboradas que respondan a nuevos fenómenos oscilatorios más complejos algunos de los cuales presentan un gran interés en ciencia y tecnología. El estudio y análisis de la composición de oscilaciones y sus aplicaciones, es un tema amplio. En la práctica se puede tratar la superposición de oscilaciones con diferentes pulsaciones, desfases o amplitudes, bien en la misma dirección, bien en diferentes direcciones dentro del plano o más complejo todavía, situar dicha superposición en el espacio de tres dimensiones. El campo de la superposición de oscilaciones es muy amplio. En la práctica se pueden superponer varios M.A.S., de diferentes pulsaciones y con diferentes orientaciones entre sí. Sin embargo, aquí solo se van a exponer los que presentan más interés en la práctica, que, por ende, son los que resultan más sencillos de tratar matemática y físicamente: superposición de dos M.A.S. en la misma dirección con la misma pulsación o con pulsaciones diferentes pero próximas y en direcciones perpendiculares(de la misma pulsación o de pulsaciones múltiplo la una de la otra).
Las superposiciones más básicas son las de dos osciladores que realizan cada uno un M.A.S. El resultado, en general, ya no es un M.A.S. pero la oscilación resultante puede ser de gran interés tanto práctico como de fundamento para comprender el fenómeno ondulatorio. Entre ellas, las de más interés que se detallarán más adelante, son básicamente de tres tipos:
Si se libera la imposición, para ambas oscilaciones de partida, de que tengan la misma pulsación ω, el movimiento resultante, más complejo todavía, podría realizarse de manera “caótica” rellenando un espacio acotado por las amplitudes de las oscilaciones que se superponen. Pero si la relación entre pulsaciones es un número entero (una es un múltiplo de la otra) entonces dará lugar a unas curvas especiales denominadas figuras de Lissajouss. Estas dos propiedades importantes, la polarización de ondas (al observarla en una posición dada, la onda es ya una oscilación) y las figuras de Lissajouss, surgen del mismo tratamiento matemático de la superposición de oscilaciones.
Tanto para analizar la superposición de oscilaciones como para las oscilaciones en general, se pueden emplear diversos procedimientos matemáticos que pueden contribuir a facilitar el estudio y comprender mejor el significado físico de los mismos. El más inmediato consiste en manejar las expresiones algébricas, para las diferentes composiciones, como se ha venido realizando hasta ahora. Otros procedimientos consisten en analizar las oscilaciones en el plano complejo, empleando exponenciales imaginarias, o bien operar con fasores en dicho plano complejo CITA. Los fasores, son números complejos z=a+ib tal que i es la unidad imaginaria, que están representados en el plano complejo por un módulo y un argumento a modo de un vector que gira con velocidad angular ω. De esta manera podremos, por ejemplo, sumar dos fasores a modo de vectores. Sin embargo, a diferencia de los vectores en el plano, los fasores si tienen definida la operación ‘inverso de un fasor z’, ya que el plano complejo, a su vez, tiene la estructura matemática de cuerpo. Ventaja que se aprovecha para operar con la ley de Ohm en el plano complejo en análisis de circuitos eléctricos, operando así de forma simultánea, en las operaciones de multiplicación y división, con todo el fasor (módulo y el ángulo de fase del fasor o argumento). Por el contrario, no está definida la operación del inverso de un vector por lo que la equivalencia de un fasor con un vector en el plano, tiene lugar solamente en las operaciones de suma y resta.
Una forma gráfica de introducir estos procedimientos y conceptos, como hemos comentado anteriormente, consiste en comprobar que la proyección de un movimiento circular uniforme de velocidad angular ω sobre un diámetro cualquiera de la trayectoria circular, es un M.A.S. de pulsación ω. Dicha proyección se suele realizar a lo largo de uno de los ejes coordenados en el plano. La facilidad para comprender las oscilaciones y su composición, viene de la mano del conocimiento del movimiento circular uniforme y conduce al empleo de estas técnicas.

Si bien esta composición de oscilaciones implica la realización de una serie de operaciones matemáticas, conviene no perder de vista las aplicaciones físicas básicas que traen consigo. Como ejemplo de esta composición, se puede imaginar el movimiento de la aguja de un trazador gráfico o Plóter. Por un lado éste debe dibujar un M.A.S. a lo largo del eje horizontal y por otro lado, debe dibujar un M.A.S. en la dirección del eje vertical, ambos con la misma pulsación ω y este segundo con un desfase relativo δ respecto del primero, de manera que el origen de coordenadas para ambos movimientos sea el (x,y)= (0,0). Se plantean dos preguntas: ¿qué movimiento resultante realizará? Y ¿qué dibujo resultará? El resultado depende del desfase relativo δ entre ambos movimientos. Si, por ejemplo, se supone δ=0, esto significa que para t=0 el dibujo comienza en el origen de coordenadas. Si, por ejemplo, δ=π/2, significa que el movimiento en x, para comenzar el dibujo, parte de x=0, sin embargo, el movimiento vertical, para comenzar el dibujo, parte del valor máximo y=B; por tanto, el movimiento parte del punto (0, B). Se van a superponer las dos oscilaciones x(t) e y(t), , y a comprobar matemáticamente cuál es el resultado de la composición. Para ello, se van a desarrollar las expresiones armónicas en seno y coseno con la finalidad de eliminar el tiempo para obtener y (x). Sustituyendo la variable ‘y’ como función de la ‘x’ eliminando el tiempo entre las dos expresiones, se puede obtener la trayectoria descrita por la aguja en el plano (x,y). En efecto,
, es decir,
.
Si ahora se opera con la variable ‘y’ como función de la variable ‘x’, dejando en un miembro solamente el término de la raíz cuadrada y elevando toda la expresión que resulta al cuadrado, obtenemos el siguiente resultado:
.
Esta expresión obtenida es una función cuadrática en ‘x’ e ‘y’ que se puede explorar dando valores al desfase relativo δ. Se observa fácilmente que si δ=0, π, el resultado es la ecuación. Con el signo + (δ=0) es la ecuación de una recta que representa la diagonal de pendiente positiva del rectángulo de lados A,B centrado en el origen de coordenadas y con el signo - (δ= π) representa la ecuación de una recta que es la diagonal de pendiente negativa del citado rectángulo. El movimiento resultante, es periódico y se realiza sobre el citado segmento de recta. Por ello, cuando se aplica al fenómeno ondulatorio y las ondas que se superponen en un punto del espacio son transversales, dará lugar en dicho punto a la polarización rectilínea de la onda. Al poder oscilar transversalmente a la dirección del movimiento, por ejemplo eje x, la oscilación resultante se puede realizar en el plano perpendicular, plano yz. Sin embargo, este resultado implica que su oscilación en el tiempo queda confinado a una recta (en el caso analizado siguiendo las dos rectas de pendiente positiva y negativa respectivamente). Se puede estudiar también los otros dos casos de interés, cuando δ= π/2, 3π/2. Si se sustituyen estos valores de δ en la función cuadrática en ‘x’ e ‘y’ obtenida, resulta la siguiente ecuación : .
Es la ecuación canónica de una elipse de ejes principales, los ejes coordenados. Si A=B, el resultado es la ecuación de una circunferencia de radio A. La oscilación resultante evolucionará en el tiempo dando los valores de la elipse o de la circunferencia, en su caso, para cada ‘y’ en función de ‘x’, dependiendo de los valores de las amplitudes A y B. Al tratar con la superposición de las ondas en una posición fija y con las citadas condiciones, el resultado será el de una onda resultante polarizada elíptica, o circularmente, respectivamente. A través del ejemplo de la trazadora gráfica y operando con la superposición de dos M.A.S. con la misma pulsación ω y en direcciones perpendiculares se puede apreciar en el plano un resultado que corresponde al del fenómeno de polarización de la onda resultante, en el punto dado del espacio, cuando interfieren dos ondas transversales, por ejemplo las ondas electromagnéticas. Esta composición también se puede apreciar gráficamente al evolucionar el punto que describe el movimiento resultante en la tercera dirección del espacio, el eje z, en función del tiempo con velocidad v constante. En caso de una circunferencia (segundo caso), el resultado será un movimiento helicoidal uniforme con un paso de la hélice p = v.T= v (2π/ω).

Es un caso sencillo pero importante. Se consideran dos M.A.S. de la misma frecuencia angular ω pero con diferentes amplitudes y fases, ambos orientados en la dirección x
y
Si se emplea la notación de los vectores rotatorios, en la figura se observa que el primer M.A.S. viene representado por el vector giratorio azul y el segundo M.A.S por el vector giratorio rojo. El ángulo formado por el vector azul con el origen de ángulos es y el formado por el vector rojo es . Los dos vectores giran con la misma ω luego su posición relativa se mantiene constante, con un ángulo de fase constante . El M.A.S. resultante se obtendrá mediante la superposición
La superposición de los dos M.A.S. se puede realizar geométricamente sumando vectorialmente los dos vectores componentes tal como se puede observar en la construcción vectorial de la figura. El resultado de la suma es el vector de color violeta que también girará con la misma velocidad angular ω. El argumento del vector giratorio violeta, será de la forma y el diagrama vectorial permitirá determinar .
y la amplitud
Más interesante que expresar las fases de forma absoluta y resulta elegir las expresiones de los M.A.S. en función de la diferencia de fase entre ambos . Las fórmulas anteriores quedan así:
Tres casos importantes se pueden deducir:
1.º- Dos M.A.S. en fase () caso que proporciona y . Los fasores asociados a A1 y A2 estarían en la misma dirección y el mismo sentido, sumándose directamente.
2.º- Dos M.A.S. en oposición de fase ()caso que proporciona y . Los fasores asociados a A1 y A2 estarían en la misma dirección y sentidos opuestos, restándose directamente.
3.º- Dos M.A.S. en cuadratura ()caso que proporciona y si en este segundo caso se verifica además entonces ()y .

Esta composición es importante como aplicación al fenómeno de interferencia de ondas de cualquier tipo, procedentes de dos focos puntuales distintos[13]. Si las ondas procedentes de los dos focos tienen la misma pulsación , los dos focos mantienen una diferencia de fase constante entre ellos (condición de coherencia) y se superponen en una posición dada del espacio, el efecto resultante, es un movimiento oscilatorio con la misma pulsación y la intensidad media de la onda resultante en el citado punto es proporcional a la amplitud resultante al cuadrado:, donde c es una constante. La superposición de las ondas que cumplen la condición de coherencia formarán un patrón de interferencias cuya distribución de intensidad es estable. La amplitud de la oscilación resultante en cada punto se obtiene fácilmente con la técnica de fasores como se puede apreciar en la figura de la composición, ya que dependerá del desfase de los movimientos que se componen. Analíticamente:
;
A partir de la última expresión se pueden obtener los máximos y los mínimos de intensidad en la región de la superposición:
Máximos de Intensidad : => ; n=0,1,2...
Mínimos de Intensidad: => ; n=0,1,2...
Las pulsaciones o batidos es un fenómeno ondulatorio que se puede apreciar con ondas sonoras. Se genera al superponer en un punto del espacio dos ondas sinusoidales con frecuencias ligeramente distintas. Al realizar la superposición en un punto del espacio fijo lo que tiene lugar en ese punto es la superposición de dos oscilaciones en el tiempo.
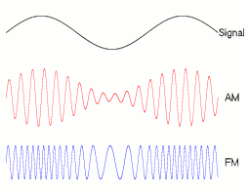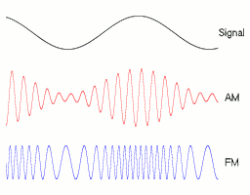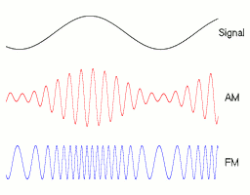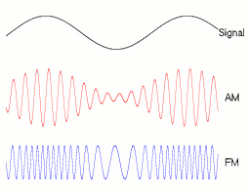
Por tanto, se van a considerar dos M.A.S. con la misma fase inicial y distinta pulsación:
La superposición de ambos puede expresar como:
y da origen a la pulsación:
en la que A(t) es la amplitud dependiente del tiempo en forma armónica:
.
Es importante resaltar que el resultado de la composición ya no es M.A.S ya que su amplitud A, como se ha comentado, no es constante sino que depende de forma armónica en el tiempo resultando una oscilación en forma de pulsos. En particular, cuando , el movimiento resultante tiene la siguiente expresión:
,
con una pulsación para el movimiento resultante:
,
y la pulsación para la amplitud A(t) (que tiene la forma de un M.A.S.):
.
El fenómeno oscilatorio recogido aquí también se puede aplicar a la Amplitud_modulada AM que se realiza con ondas de radio y TV y que se puede apreciar en la figura.
Es interesante reflexionar sobre el contenido físico de las oscilaciones y como queda recogido en las expresiones analíticas que las describen. Resulta muy cómodo esforzarse por encontrar un buen modelo matemático para describir un fenómeno físico y a partir de ese momento pasar el trabajo a depender de una aplicación sistemática de las matemáticas. No es bueno, sin embargo, perder de vista o dejar aplazado el sentido físico del problema. Un seguimiento físico de la evolución de las ecuaciones puede ayudar a evitar errores analíticos o de cálculo. Por otro lado es interesante consignar que cuando los matemáticos toman en consideración el estudio, por ejemplo, de una ecuación diferencial modelo y a pesar de su razonamiento más abstracto, procuran resaltar el papel desarrollado por la misma en el campo de las ciencias o las técnicas. El tema de las oscilaciones se presta muy bien a razonar sobre las ecuaciones diferenciales que las describen, las soluciones de las mismas y la repercusión del propio sistema físico o del papel del experimentador en sus expresiones analíticas. Dentro del campo de las oscilaciones se han manejado tres ecuaciones diferenciales modelo correspondientes a:
En los tres casos existe una interpretación física directamente implicada en su formulación matemática y una necesidad de incorporar unas condiciones iniciales (en un caso general unas condiciones temporales) para la descripción analítica completa del fenómeno. Aquí se reúnen las ecuaciones diferenciales que describen los tres tipos de oscilaciones referidas a un ejemplo estándar ampliamente empleado para introducir el estudio de estas como es el caso del resorte de constante recuperadora k con una masa m en su extremo:
Al observar conjuntamente las tres ecuaciones se pueden hacer algunas observaciones. Todos los términos de las ecuaciones así expresadas son fuerzas o poseen dimensiones de fuerzas, sus coeficientes son características propias del sistema físico y cada ecuación procede de una aplicación de la segunda ley de Newton al sistema físico correspondiente. También se observa cómo se va pasando del sistema con una sola fuerza elástica recuperadora , al sistema con una fuerza añadida de rozamiento viscoso y posteriormente, al sistema con una fuerza externa superpuesta de naturaleza periódica . Es lógico pensar, como así sucede, que en las soluciones de las tres ecuaciones figuren explícitamente las tres características del sistema físico , y así como las de la fuerza exterior aplicada y .
La solución de la ecuación 1) es, en una de sus formas más empleada ( porque existen otras), donde . Por consiguiente es una constante magnitud característica del sistema. Sin embargo las constantes y , amplitud y fase, respectivamente, del movimiento armónico simple, no dependen del sistema. Para determinarlas se debe acudir a dos condiciones temporales a las que se debe someter la solución o sus derivadas y , velocidad y aceleración, respectivamente. Entre la forma de seleccionar las condiciones temporales predomina el caso de elegir dos condiciones iniciales ( para ). Por ejemplo el caso muy frecuente de dar los valores de y . Hablando en términos físicos, estableciendo los valores de la posición y la velocidad iniciales. Lo cual no es óbice para que en un caso general pudiera interesar facilitar, por ejemplo, las siguientes condiciones temporales y o estas otras y .
En el caso de las fuerzas de rozamiento débiles, la solución de la ecuación 2) es con y . Se observa nuevamente que tanto γ como dependen del sistema y poseen dimensiones de tiempo a la menos uno, mientras que A y van a depender de dos condiciones iniciales (o temporales, en general). También se observa que la solución es decreciente con el tiempo lo que será común a todos los tipos de solución de la ecuación 2) debido a la existencia de la fuerza de fricción .
También en el caso de fuerzas de rozamiento débiles, la solución de la ecuación 3) es que resulta de la superposición de la solución decreciente de 2), llamada solución general, más una solución, llamada solución particular de la ecuación con segundo miembro donde aparecen tres constantes B, y . De las tres se identifica a como la frecuencia angular de la fuerza armónica exterior. Las otras dos constantes tienen las expresiones y y dimensiones respectivas de longitud y radianes. Estas últimas dependen de las características del sistema ( , y ) y de la fuerza armónica aplicada ( y ) pero no dependen de las condiciones iniciales, o temporales, en general. Las expresiones de las velocidades son las siguientes:
Se ha prestado una atención especial al caso definido como descrito por unas fuerzas disipadoras débiles el cual conserva una cierta naturaleza periódica. Es el caso que mayor interés suele ofrecer en la práctica y el más estudiado, por tanto. Analíticamente se podría describir un caso donde y, por tanto . También puede darse el caso de un sistema sometido a unas fuerzas de fricción intensas ( ) en cuyo caso adquiere un valor imaginario y, por tanto, la solución ya no posee naturaleza periódica. También carece de naturaleza armónica el caso de transición entre ambos extremos, el caso de . Los movimientos originados en estos dos casos se llaman aperiódicos y, concretamente, el de transición, aperiódico crítico. Las soluciones analíticas correspondientes a estos dos casos son decrecientes y vienen dadas por las expresiones:
para y para
Como en los casos anteriores también ahora figuran explícitamente los parámetros característicos del sistema y , y dos constantes A y B para ser determinadas por dos condiciones temporales, generalmente dos condiciones iniciales. Aunque las constantes en ambas soluciones han recibido los mismos nombres A y B, obsérvese que todas ellas poseen dimensiones de longitud, excepto la A de la segunda solución que posee dimensiones de velocidad. Las expresiones de la velocidad v de los dos casos son las siguientes:
para y
para . Al igual que las elongaciones, también las velocidades son decrecientes con el tiempo.
Un sistema oscilante muy ilustrativo consiste en un circuito eléctrico donde se combinan en serie un condensador de capacidad C, una autoinducción L y una resistencia R[14]. Hay muchas otras variantes de circuitos eléctricos oscilantes, pero el descrito es el más sencillo de estudiar tanto en el aspecto físico como matemático. Como en el modelo mecánico seleccionado entre otros muchos, el eléctrico citado permite su implementación simple y su estudio en el laboratorio. También aquí se pueden estudiar los regímenes libres o el régimen forzado si se eligen convenientemente los valores de las componentes del circuito. Una forma cómoda de iniciar el estudio consiste en montar en serie un condensador con una resistencia y una autoinducción. Con un sentido práctico se añade un interruptor que permanece abierto hasta dar comienzo el estudio del fenómeno libre. Para empezar y antes de que el circuito comience a evolucionar, se debe suministrar energía al circuito. Una forma cómoda de hacerlo consiste en cargar el condensador inicialmente con una carga Q.
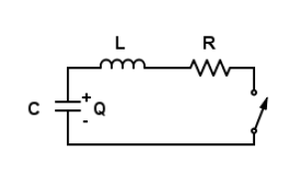
Al cerrar el interruptor la carga del condensador inicialmente Q, empieza a pasar al circuito en forma de una corriente i y se desencadena un régimen decreciente, tanto de la corriente como de la carga del condensador y otras variables eléctricas. La existencia de una resistencia como elemento disipador de la energía es la que anuncia la aparición de un régimen decreciente. El que sea de naturaleza oscilante o no depende de los valores concretos de R, L, y C. La ecuación que describe el comportamiento del circuito a partir del instante en que se cierra el interruptor consiste en una Ley de Ohm adaptada al circuito:
Donde q representa la carga que conserva el condensador e i la corriente que circula por el circuito, ambas en un instante t.

El primer miembro representa el término que hace el papel de fuerza electromotriz de alimentación del circuito en un instante t seguido de la fuerza contraelectromotriz inducida generada en la autoinducción al paso de la corriente i de descarga del condensador . Conviene emplear una sola variable independiente. Para relacionar la carga del condensador con la corriente del circuito i, hay que tener en cuenta que la carga que el condensador ha cedido al circuito es Q-q por lo tanto:
Y también:
Llevando estos valores a la ley de Ohm de partida se obtiene:
Se puede observar que esta ecuación corresponde al régimen decreciente descrito por la carga q del condensador. La misma ecuación puede ser expresada en términos de la corriente i:
Esta es una ecuación íntegro-diferencial donde cada término representa el potencial en cada uno de los tres elementos del circuito. Para su resolución se suele derivar respecto al tiempo, quedando:
La ecuación obtenida no tiene un sentido físico claro como las ecuaciones precedentes, la ecuación íntegro-diferencial o la ecuación en q, sin embargo se presta a su resolución de forma inmediata. Una forma equivalente es:
Al analizar esta ecuación diferencial de segundo orden y coeficientes constantes se observa que los regímenes que puede sufrir son los mismos que en el sistema mecánico estudiado consistente en una masa m en el extremo de un resorte de constante recuperadora k y una fuerza de rozamiento viscosa. Los parámetros que describen el sistema adquieren ahora los valores:
, ,
La ecuación anterior se puede poner en la forma:
Y es la que se suele emplear para caracterizar el circuito R, L, C serie. Si se compara con la del resorte () se observa que es la misma salvo que allí la variable es x, posición de la masa m, y aquí es la corriente que circula por el circuito R, L, C serie. La solución de la ecuación en el caso correspondería al régimen oscilante decreciente:
Donde ahora la amplitud representa la corriente que circula por el circuito en t = 0.
Para generar un régimen forzado habría que colocar un generador de fuerza electromotriz en serie con R, L y C

y se tendría la siguiente ecuación diferencial:
donde todos los términos tienen un sentido físico claro. Si se deriva respecto al tiempo miembro a miembro
y se divide por L adquiere la forma ecuación que resuelta proporciona la corriente que circulará por el circuito R, L, C forzado. Este circuito R, L, C forzado una f.e.m. alterna en serie, se conoce también como circuito R, L, C serie de corriente alterna (c.a.). La solución completa será la suma de una corriente decreciente correspondiente al régimen libre y una corriente oscilatoria y permanente de pulsación () correspondiente al régimen forzado que es la que predomina al cabo de un tiempo largo cuando desaparece el transitorio. En el supuesto de un régimen oscilante decreciente , que es la parte del transitorio, la solución completa tiene la forma:
Donde y .
Al cabo de un tiempo suficientemente largo, desaparece el transitorio y queda la solución del régimen forzado permanente para el circuito R, L, C serie de c.a.
La amplitud de la corriente en el circuito R, L, C forzado sigue una ley que presenta un pico de resonancia[15][13]. El citado pico aparece cuando la frecuencia angular externa es igual a la pulsación natural del circuito , esto es, , con un valor correspondiente para la corriente igual a la máxima de . Esta es la condición de resonancia del circuito de c.a. R, L, C serie, de tanto interés, por ejemplo, en los circuitos sintonizadores de antena para receptores de radio y televisión.[16] Variando la pulsación exterior en se anula . Se trataría en este caso de intentar alimentar el circuito R, L, C con una tensión constante y el condensador impediría la circulación de la corriente en régimen permanente.
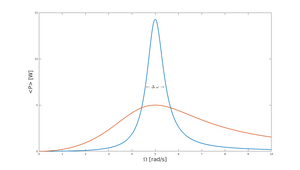
El único elemento del circuito que consume energía es la resistencia. La potencia instantánea consumida en el circuito R, L, C serie será Y la potencia media absorbida por el circuito en un periodo se consume íntegramente en la resistencia. También sigue una ley que presenta un pico de resonancia
representa el valor de la potencia media máxima, que tiene lugar en el pico de la resonancia el cual se presenta para . La curva de resonancia en potencia media consumida también pasa por el origen .
La anchura de banda (que representa el rango de frecuencias en las que el circuito absorbe energía de manera importante) en función del factor de calidad Q se puede expresar de la siguiente forma: donde representa la anchura del pico tomada a mitad de su altura (ver figura). Por ello, un valor alto de reflejará la agudeza y estrechez del pico de la resonancia indicando la bondad del oscilador, poco amortiguado. Fijada la frecuencia de oscilación del circuito, a mayor Q, menor ancho de banda y viceversa.
El factor de calidad[17] Q indica la calidad de un oscilador, a mayor valor, menos amortiguado y, por tanto, mejor oscilador es y viceversa. Se va a desarrollar su expresión para el oscilador eléctrico R, L, C serie que ofrece gran interés interés en frecuencias próximas a la de resonancia debido a la forma de la curva de la resonancia en el entorno de su máximo y al papel jugado por el ancho de banda de la curva de resonancia. Situados sobre las curvas de resonancia para la potencia se verificará para el factor de calidad[18] donde representa la anchura del pico de la resonancia a mitad de su altura . Sustituyendo los valores de la pulsación de resonancia y el coeficiente de atenuación que corresponden al circuito R, L, C serie se obtiene el factor de calidad, donde se observa que el factor de calidad es inversamente proporcional al valor del elemento disipativo de la energía del circuito, que es la resistencia.
Los circuitos serie se utilizan para responder selectivamente a las señales eléctricas de una frecuencia dada (para esta aporta una potencia elevada), mientras discrimina las señales de otras frecuencias (les aporta una potencia muy débil). El "factor de calidad" Q es una forma de medir esa selectividad.
Otra característica de estos circuitos es la anchura de banda que se representa por y así aparece en la curva de resonancia para la . Representa el margen de frecuencias dentro del cual el circuito trabaja con valores razonables de potencia (superiores a ). De la propia expresión del se deduce el producto , lo que indica que, para un circuito R,L,C dado y, por tanto, con un valor de determinado, un factor de calidad alto exige una anchura de banda estrecha y viceversa, una anchura de banda amplia conduce a un factor de calidad bajo.
Con frecuencia se expresan y en función del . La primera de ellas indica que la altura es directamente proporcional al . La segunda dependencia permite trazar la familia de curvas de resonancia del circuito R, L, C serie para la potencia media en función de la frecuencia angular forzada para curvas con diferentes valores de .
Una interesante aplicación del concepto de resonancia eléctrica aparece en el fundamento de la radio, en concreto en la operación de "sintonizar la radio". En esta operación se mueve el dial de la radio ajustando la frecuencia natural del circuito a la portadora de la emisora que se desea , obteniendo en ese momento, . Representa la situación de sintonía de la radio, en las proximidades del pico de la resonancia, es cuando será mayor la amplitud de la señal captada. El mismo concepto está implicado en cualquier sintonizador de ondas e-m, por ejemplo, en la sintonización de la TV. Cuanto mayor sea el del circuito de sintonización, mayor será la potencia de la señal captada.[16]
Se denomina resonancia orbital al fenómeno en el que dos cuerpos celestes presentan períodos (tiempo de recorrido de sus órbitas) cuya razón es una fracción racional de dos números enteros, que puede reforzar y estabilizar sus órbitas o bien, contribuir a su desestabilización. Esta relación entre periodos es la inversa de la relación entre sus frecuencias de giro, que también se usa como referencia, como se hará en esta sección. Conviene recordar aquí la relación directa que hay entre los movimientos oscilatorios y los movimientos circulares no solo por ser periódicos sino porque un movimiento oscilatorio armónico se puede representar de manera unívoca como la proyección en un eje de un movimiento circular uniforme, como se puede apreciar en la imagen de la sección 6.2B. Además, las trayectorias de la mayoría de los cuerpos celestes que forman el sistema solar, si bien son elípticas, se aproximan bastante a trayectorias circulares debido a su pequeña excentricidad. Un ejemplo de resonancia orbital es la resonancia 5:2 existente entre Júpiter y Saturno, es decir, cada 5 vueltas de Júpiter alrededor del Sol, Saturno da 2 (esta es una relación entre sus frecuencias). Esta resonancia fue la causante de la creación de los anillos de Saturno. Dichos anillos están formados por fragmentos de objetos que se encontraban en el Cinturón de Kuiper. La órbita de estos objetos se distorsionó debido a la resonancia entre Júpiter y Saturno, atrayéndolos hacia el interior del Sistema Solar. Sería en este viaje hacia el interior donde quedarían orbitando alrededor de Saturno, creando los anillos del planeta.
La resonancia orbital, en un sistema planetario, actúa en ocasiones como agente estabilizador de determinadas órbitas, y en otras, por el contrario, desestabilizador de las mismas, como sucede en la formación de la gran separación o hueco que hay entre los anillos A (exterior) y B (interior) de Saturno que forman la división de Cassini. También ocurre en la formación de los huecos de Kirkwood. Júpiter, además de su resonancia con Saturno, tiene asociado otro fenómeno relacionado con la resonancia orbital, los huecos de Kirkwood en el cinturón principal de asteroides del sistema solar. Estos huecos coinciden con las resonancias 3:1, 5:2, 7:3 y 2:1. Si algún asteroide intentara alojarse en alguna de estas órbitas, la cercanía de Júpiter provocaría que saliese expulsado a otras órbitas.
En el estudio de la resonancia orbital de satélites bajo la acción de su planeta y del sol (en el sistema solar) es importante tener en cuenta el efecto de la presión de radiación debida al sol (Efecto Poynting-Robertson).[19] En el caso de la Tierra afecta al movimiento de los satélites geosíncronos. Siendo, en definitiva, la resonancia orbital responsable, en gran parte, de la formación y funcionamiento de nuestro sistema solar y también de interés en las posibles aplicaciones a satélites artificiales.