Knowledge Base Wiki

La generatriu és una línia que a causa del seu moviment conforma una figura geomètrica, que al seu torn depèn de la directriu. La generatriu pot ser una línia recta o corba.^[1]

Si la generatriu és una línia recta que gira respecte d'una altra recta directriu, anomenada eix de rotació, conformarà una superfície cònica, cilíndrica, etc. Si la generatriu és una corba, genera una esfera, un el·lipsoide, etc. Si es desplaça sobre una o més directrius, genera una superfície reglada.

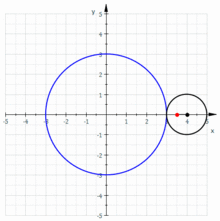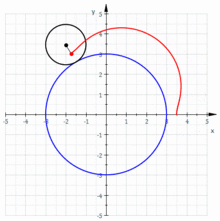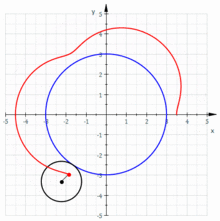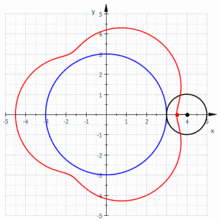
La generatriu pot ser una línia corba, per exemple, una circumferència que roda sobre una altra circumferència directriu, tangencialment. Un punt vinculat a ella descriu una trajectòria corba que s'anomena ruleta cicloidal.

• Cicloide, la corba plana generada per un punt d'una circumferència generatriu en rodar sobre una línia recta, sense lliscar.
• Epicicloide, la corba que descriu un punt vinculat a una circumferència generatriu que roda –sense lliscament– sobre una circumferència directriu, tangencialment.
• Hipocicloide, la corba que descriu la trajectòria d'un punt situat sobre una circumferència generatriu que roda per l'interior d'una altra circumferència directriu, sense lliscament.

• Trocoide, la corba plana que descriu un punt, vinculat a una circumferència generatriu , que roda sobre una línia recta directriu, tangencialment, sense lliscament.
• Epitrocoide, la corba que descriu un punt vinculat a una circumferència generatriu que roda –sense lliscament– sobre una circumferència directriu, tangencialment.
• Hipotrocoide, la corba plana que descriu un punt vinculat a una circumferència generatriu que roda dins d'una circumferència directriu, tangencialment, sense lliscament.

El cilindre és un cos de revolució engendrat per un rectangle en girar al voltant d'un dels seus costats, que serà l'altura del cilindre, i el costat oposat serà la generatriu. Per tant l'altura del cilindre serà igual a la generatriu.

h = g

El con és un cos de revolució engendrat per un triangle rectangle en girar al voltant d'un dels seus catets, que serà l'alçada del con, i la hipotenusa serà la generatriu.

Pel teorema de Pitàgores la generatriu del con és igual a g²=h²+r².

El tronc de con és un cos de revolució engendrat per un trapezi rectangle en girar al voltant del costat perpendicular a les bases, que serà l'alçada del con, i l'altre costat serà la generatriu.

Obtenim la generatriu del tronc de con aplicant el teorema de Pitàgores al triangle ombrejat: g ² = h ²+(R-r) ²