Infrastructure tools to support an effective radiation oncology learning health system

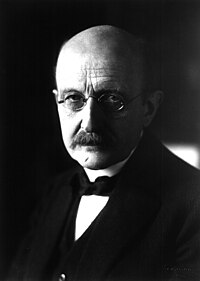
Kvantemekanikk er en teori i fysikken som beskriver og forklarer egenskapene til atomer, elementærpartikler og kreftene mellom dem. Den gir dermed en forståelse av hvordan materien er oppbygd og danner dermed grunnlaget for all kjemi. Samtidig kan teorien gi en forståelse av forholdene fra det innerste av atomkjerner til de første brøkdeler av et sekund etter Big Bang. På grunn av sine mange forskjellige anvendelser blir den også mer generelt omtalt som kvantefysikk.

I motsetning til klassisk fysikk hvor materien er bygget opp av diskrete punktpartikler som beveger seg deterministisk ifølge Newtons lover og elektromagnetisk stråling er bølger som befinner seg overalt og beskrives ved Maxwells ligninger, vil partikler i kvantemekanikken også ha bølgeegenskaper og stråling ha partikkelegenskaper. Det ble først påvist av Max Planck gjennom hans studier av sort stråling i 1900 og benyttet av Albert Einstein i 1905 til å forklare den fotoelektriske effekten. Den viser at lys består av partikkellignende kvant eller fotoner.

Bølgeegenskapene til partikler ble foreslått i 1923 av Louis de Broglie og formalisert med bølgeligningen til Erwin Schrödinger i 1926. En diskret, algebraisk og ekvivalent formulering av denne nye kvantemekanikken var funnet av Werner Heisenberg året før og kalles vanligvis for matrisemekanikk. Fellesbetegnelsen kvantemekanikk var innført av Max Born allerede i 1924.

En enhetlig beskrivelse av både partikler og stråling ble etablert i årene som fulgte og omtales som kvantefeltteori. For hver partikkeltype eller form av stråling finnes det tilsvarende, kontinuerlige felt som eksisterer overalt og er beskrevet ved klassiske bølgeligninger. Når de kvantiseres, vil kvantene være diskrete partikler som for eksempel fotoner, elektroner eller kvarker. Da disse feltteoriene kan formuleres i overenstemmelse med Einsteins spesielle relativitetsteori, vil de automatisk også beskrive de tilsvarende antipartikler. Det ble først vist av Paul Dirac i 1928 og markerer avslutningen på kvantemekanikkens etableringsfase.

Storparten av fundamental forskning i fysikk og kjemi i dag kan sies å være nye anvendelser av kvantemekanikk. Den har hatt stor betydning for den teknologiske utvikling da all moderne elektronikk og utvikling av nye, syntetiske material er basert på dens prinsipper. Det samme kan man si om superledning og dagens utvikling av nye kvantedatamaskiner.

Plancks kvant

Ved inngangen til 1900-tallet var Maxwells teori for elektromagnetisk stråling generelt akseptert. Selv om den ikke kunne gi noen forklaring på diskrete linjespekter i lys fra forskjellige substanser eller alle egenskapene ved varmestråling, mente de fleste at dette ikke var et problem ved den elektromagnetiske teorien, men hadde sin grunn i en manglende forståelse av materiens oppbygning. Man visste at atomene inneholdt elektroner etter at de var oppdaget av J.J. Thomson i 1897 og den forklaring Hendrik Lorentz på samme tid hadde gitt av den normale Zeeman-effekten.^[1]

Begynnelsen til det som senere fikk navnet kvantemekanikk, ble skapt av Max Planck på slutten av året 1900. For å forklare nye målinger av energien i varmestråling ved enda lengre bølgelengder enn tidligere, måtte han anta at atomene i veggene som omsluttet strålingen, absorberer og emmiterer denne i diskrete porsjoner som han ga navnet kvant. For stråling med frekvens ν, er energien til et slikt kvant gitt ved formelen

E=h\nu

hvor konstanten h som han måtte innføre, siden er blitt omtalt som Plancks konstant. Den opptrer i alle forbindelser der kvantemekanikken er gjeldende. Selv om vekselvirkningen med materien skjer på denne diskrete måten, mente Planck at selve strålingen fortsatt måtte betraktes som kontinuerlige bølger styrt av Maxwells ligninger.^[2]

Einsteins foton

Vekselvirkningen mellom lys og materie kommer direkte til uttrykk i den fotoelektriske effekten hvor elektron blir slått ut av metalliske overflater ved absorpsjon av ultraviolett lys. Dette fenomenet ga Einstein i 1905 en radikal forklaring ved å videreføre Plancks antagelse om diskrete energikvant i en slik prosess. Han viste ved termodynamiske argument at Plancks strålingslov kan forstås på en måte der energien i strålingen er fordelt i rommet på en diskontinuerlig måte. Mer presist, med hans egne ord består den av

.. einer endlichen Zahl in Raumpunkten lokalisierten Energiequanten, welche sich bewegen, ohne sich zu teilen, und nur als Ganze absorbiert und erzeugt werden können.
A. Einstein, 1905.^[3]

Dette er første beskrivelse av hva som fra 1926 skulle ble kalt et foton. I motstrid med Plancks overbevisning mente Einstein at Maxwells teori for elektromagnetisk stråling ikke lenger kan benyttes, i alle fall ikke i denne sammenheng.^[1]

Videre betraktninger av emisjon og absorpsjon av lys basert på statistisk mekanikk førte Einstein i 1909 til å konkludere med at et foton med bølgelengde λ = c /ν har impuls

p={h \over \lambda }

De er derfor masseløse partikler som følger fra hans spesiell relativitetsteori da E = pc.

Samme år viste han ved lignende betraktninger at fluktuasjoner i energien til varmestrålingen består av to ledd som viser at den kan beskrives som en gass av partikler som samtidig har både egenskaper som klassiske partikler og bølger. Dette var første uttrykk for bølge-partikkel dualisme som i kvantemekanikken også gjelder for massive partikler.

I en serie med forelesninger i nyere tid har Richard Feynman sagt at lys ganske enkelt består av fotoner. Den konklusjonen er han kommet frem til ved å betrakte lys som sendes mot en flate som består av veldig små fotoceller. Når lysintensiteten blir tilstrekkelig lav, vil disse tennes én og én og ikke flere samtidig. Det viser at energien i strålingen befinner seg i små, lokaliserte pakker. Hvert slikt masseløst foton er en partikkel bortsett fra at den beveger seg ifølge kvantemekanikkens lover istedenfor klassisk mekanikk. Det forklarer at lys som inneholder mange fotoner, kan fremvise de klassiske bølgefenomenene som interferens og diffraksjon.^[4]

Atommodeller

To år etter at Ernest Rutherford oppdaget at hvert atom har en kjerne som inneholder storparten av dets masse og er mye mindre enn dets størrelse, kunne Niels Bohr i 1913 forklare de diskrete frekvensene i lyset fra hydrogenatomet ved bruk av sin atommodell. Denne la også grunnlaget for en forståelse av mer kompliserte atom.^[1]

Modellen var basert på to radikale antagelser:

1) Elektronet kan bevege seg i stasjonære sirkelbaner med konstant energi uten å emittere lys.

2) Dreieimpulsen L = mrv til elektronet i en bane med radius r og hastighet v kan bare ta diskrete verdier

L=n{h \over 2\pi }

hvor kvantetallet n kun kan ta diskrete verdier n = 1, 2, 3 og så videre.

I tillegg gjorde han bruk av Plancks oppdagelse om emisjon og absorpsjon av lys i diskrete kvant. For atomet betyr det at ved elektronets overgang fra en bane med energi E til en annen bane med energi E' , sendes det ut et foton med frekvens ν som er bestemt ved betingelsen

E-E'=h\nu

Allerede i 1914 viste Franck-Hertz eksperimentet at atomene inneholder slike diskrete energitilstander.

Den første antagelsen ble beholdt i den senere videreføring av kvantemekanikken hvor den tilsvarer eksistensen av stasjonære kvantetilstander. Derimot viste den andre antagelsen seg snart å være utilstrekkelig for å forstå mer detaljerte egenskaper ved atomene.^[5]

Bohr-Sommerfelds kvantisering

Elektronet i hydrogenatomet blir holdt på plass ved den elektriske Coulomb-kraften fra atomkjernen på samme måte som planetenes gang er styrt av tyngdekraften fra Solen. Begge disse krefter varierer på samme måte med avstanden slik at også et elektron burde kunne bevege seg i en ellipsebane på tilsvarende måte som en planet ifølge Keplers lover.

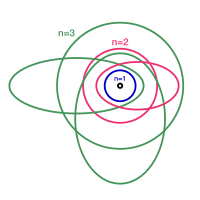
Arnold Sommerfeld foreslo i 1916 å inkludere slike ellipsebaner blandt de stasjonære banene for elektronet i H-atomet. Han ble nødt til å innføre en mer generell kvantisering av disse banene basert på kanoniske impulser i analytisk mekanikk. For hver koordinat q_i som beskriver en partikkels posisjon, finnes det en tilsvarende konjugert impuls p_i. Sommerfeld antok at disse kunne bare ta diskrete verdier gitt ved integralbetingelsen

\oint \!dq_{i}\,p_{i}=n_{i}h

hvor n_i er heltallige kvantetall. For en sirkulær bane i planet gitt ved en asimutal vinkel φ som varierer fra 0 til 2π , er den konjugerte impulsen dreieimpulsen L. I dette spesielle tilfellet gir betingelsen dermed 2π L = nh som er i overensstemmelse med hva Bohr hadde antatt. Disse mer generelle kvantebetingelsene blir derfor omtalt som Bohr-Sommerfeld-kvantisering.^[6]

Når ett elektron beveger seg i tre dimensjoner omkring atomkjernen, vil det i denne atommodellen til Sommerfeld nå beskrives ved tre kvantetall. De benevnes vanligvis n, k og m hvor energien til de stasjonære banene er gitt ved «hovedkvantetallet» n på samme måte som i Bohrs modell. Det «asimutale kvantetallet» bestemmer dreieimpulsen til disse banene og tar verdiene k = 1, 2, 3, .., n avhengig av hvor ellipseformet banen er. Til slutt avgjør det «magnetiske kvantetallet» m ellipsebanens orientering i rommet.

Hastigheten til elektronene i et atom har en størrelsesorden som er prosenter av lyshastigheten. Derfor vil effekter fra spesiell relativitetsteori tas med i en nøyaktig beskrivelse av deres bevegelse. Det kan gjøres ved denne mer generelle kvantiseringen, og Sommerfeld lyktes å forklare på denne måten en del av den observerte finstrukturen i spektra til flere atomer.

Detaljert forståelse av egenskapene til atomer med mange elektroner ble langsomt etablert spesielt ved studier av den karakteristiske røntgenstrålingen fra tyngre atomer og fra Zeeman-effekten til atomer i ytre magnetfelt. Det gjorde det klart at denne halvklassiske kvantefysikken måtte erstattes av en ny kvantemekanikk.^[7]

Heisenbergs matrisemekanikk

Heisenberg sammen med Niels Bohr i 1936 på hans institutt i København.

Etter sitt samarbeid med Hendrik Kramers i 1924-25 ved Bohrs institutt i København for å forstå opptisk dispersjon, var Heisenberg kommet frem at det ville være nytteløst å avdekke egenskapene til atomer ved detaljerte beskrivelser av deres klassiske baner. Man måtte i stedet konsentrere seg om deres spektrallinjer med målbare frekvenser og intensiteter. Frekvensen til fotonet som sendes ut ved en overgang mellom to tilstander m og n måtte være gitt ved Bohrs formel

\hbar \omega _{mn}=E_{m}-E_{n}

Likedan måtte intensiteten være gitt ved nye, dynamiske størrelser x_mn som erstatter koordinatene til elektronene som foretok en slik overgang. De er i alminnelighet komplekse tall som må oppfylle $x_{mn}^{*}=x_{nm}$ . På samme måte må den klassiske impulsen p til en partikkel erstattes med tilsvarende variable p_mn. Istedenfor kontinuerlige variable x og p vil derfor den nye kvantemekanikken inneholde en uendelig mange, diskrete variable.^[8]

Max Born påpekte at disse nye variable kunne kombineres på samme måte som gjelder ved matrisemultiplikasjon. Det er derfor naturlig å betrakte x_mn og p_mn som komponenter av matriser ${\hat {x}}$ og ${\hat {p}}$ . Generelt vil produktet ${\hat {x}}{\hat {p}}$ ikke være likt med ${\hat {p}}{\hat {x}}$ da det ikke er kommutativt. Derimot må disse to variable oppfylle den fysiske betingelsen

[{\hat {x}},{\hat {p}}]=i\hbar

når man definerer «kommutatoren» mellom to variable ${\hat {A}}$ og ${\hat {B}}\;$ som $[{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}$ . Alle observerbare variable eller observable vil beskrives ved slike matriser som må være «hermitiske», det vil si at matriseelementene oppfyller $A_{mn}^{*}=A_{nm}$ og skrives som ${\hat {A}}^{\dagger }={\hat {A}}.$ Den hermitisk konjugerte av et produkt bytter om på rekkefølgen av faktorene som sees fra kommutatoren mellom ${\hat {x}}$ og ${\hat {p}}.$

Heisenbergs kvantemekanikk omtales ofte som matrisemekanikk. Han benyttet den selv til å beregne de kvantiserte energiene til en harmonisk oscillator og utarbeidet approksimative resultat for en oscillator med et potensial som ikke er helt harmonisk. Sammen med Born og hans assistent Pascual Jordan ble denne nye formalismen videre utviklet.^[7]

Kvantedynamikk

En partikkel i det tredimensjonale rommet har en klassisk posisjonsvektor x = (x₁, x₂, x₃) som kvantemekanisk vil beskrives ved tre matriser ${\hat {\mathbf {x} }}=({\hat {x}}_{1},{\hat {x}}_{2},{\hat {x}}_{3})$ som kommuterer med hverandre. Tilsvarende vil impulsen beskrives ved tre kommuterende matriser ${\hat {\mathbf {p} }}=({\hat {p}}_{1},{\hat {p}}_{2},{\hat {p}}_{3}).$ Derimot kommuterer ikke koordinatvariable med impulsvaiable, men er gitt ved kommutatoren

[{\hat {x}}_{a},{\hat {p}}_{b}]=i\hbar \,\delta _{ab}

hvor Kroneckers deltasymbol inngår på høyre side. Det er denne fundamentale antagelsen som definerer den nye kvantemekanikken.

Omtrent samtidig med at Born, Heisenberg og Jordan utarbeidet dens konsekvenser, ga Paul Dirac den et fundament basert på klassisk Hamilton-mekanikk. I hans formulering ble ikke de dynamiske variable betraktet som matriser, men abstrakte, ikke-kommuterende objekt som han kalte «q-tall» eller operatorer i motsetning til de klassiske, reelle «c-tall». De fundamentale kommutatorene er da gitt mellom koordinatene ${\hat {x}}_{a}$ og deres kanonisk konjugerte impulser ${\hat {p}}_{a}.$ En kvantemekanisk kommutator mellom to dynamisk variable ${\hat {A}}=A({\hat {\mathbf {x} }},{\hat {\mathbf {p} }})$ og ${\hat {B}}=B({\hat {\mathbf {x} }},{\hat {\mathbf {p} }})$ skal ha samme form som den klassiske Poisson-klammen ved at

[{\hat {A}},{\hat {B}}]\rightarrow i\hbar \,[\!A(\mathbf {x} ,\mathbf {p} ),B(\mathbf {x} ,\mathbf {p} )]_{PB}

hvor høyresiden kan regnes ut på vanlig vis ved derivasjon. Denne sammenhengen mellom kvantemekanikk og klassisk mekanikk er et matematisk uttrykk for Bohrs korrespondanseprinsipp som Heisenberg benyttet på en ganske annen måte i sitt arbeid.^[8]

Bevegelsen til en partikkel med masse m som beveger seg i et potensial V(x) kan nå finnes ved å ta utgangspunkt i den klassiske Hamilton-funksjonen. Kvantemekanisk gir den opphav til Hamilton-operatoren

{\hat {H}}={{\hat {\mathbf {p} }}^{2} \over 2m}+V({\hat {\mathbf {x} }})

som bestemmer hvordan partikkelen beveger seg med tiden. Denne dynamiske utviklingen er nå gitt ved operatorligningene

i\hbar {d{\hat {\mathbf {x} }} \over dt}=[{\hat {\mathbf {x} }},{\hat {H}}],\;\;i\hbar {d{\hat {\mathbf {p} }} \over dt}=[{\hat {\mathbf {p} }},{\hat {H}}]

De har samme form som de klassiske Hamilton-ligningene uttrykt ved Poisson-klammer. En observabel som kommuterer med Hamilton-operatoren, vil forbli konstant under denne dynamiske utviklingen.

Derivasjon av produkt med tidsavhengige observable følger i det enkleste tilfellet fra regelen

{d \over dt}({\hat {A}}{\hat {B}})={d{\hat {A}} \over dt}{\hat {B}}+{\hat {A}}{d{\hat {B}} \over dt}

Den inverse av operatören ${\hat {A}}$ skrives som $1/{\hat {A}}={\hat {A}}^{-1}$ og er definert ved at ${\hat {A}}{\hat {A}}^{-1}={\hat {A}}^{-1}{\hat {A}}=1.$ Ved å derivere begge sidene av denne sammenhengen, finner man at

{d \over dt}{\hat {A}}^{-1}=-{\hat {A}}^{-1}{d{\hat {A}} \over dt}{\hat {A}}^{-1}

På tilsvarende vis blir $({\hat {A}}{\hat {B}})^{-1}={\hat {B}}^{-1}{\hat {A}}^{-1}.$ Denne reversering av rekkefølgen skjer også ved hermitsik konjugering av slike produkt.

Når potensialet som partikkelen beveger seg i, kun avhenger av avstanden r til origo, sies det å være sentralsymmetrisk. Klassisk er denne avstanden gitt ved r² = x_ax_a når man summerer over de to like indeksene. Ved å benytte identiteten $[{\hat {A}},{\hat {B}}{\hat {C}}]={\hat {B}}[{\hat {A}},{\hat {C}}]+[{\hat {A}},{\hat {B}}]{\hat {C}},$ finner man nå kommutatoren

[{\hat {\mathbf {p} }},{\hat {r}}^{2}]={\hat {x}}_{a}[{\hat {\mathbf {p} }},{\hat {x}}_{a}]+[{\hat {\mathbf {p} }},{\hat {x}}_{a}]{\hat {x}}_{a}=-2i\hbar {\hat {\mathbf {x} }}

Dette kan videreutvikles til å gi $[{\hat {\mathbf {p} }},{\hat {r}}^{n}]=-ni\hbar {\hat {r}}^{n-2}{\hat {\mathbf {x} }}\,$ som man kan ta som gyldig for alle verdier av n, positive og negative. Generelt har man at

[{\hat {\mathbf {p} }},V({\hat {r}})]=-i\hbar V'({\hat {r}}){{\hat {\mathbf {x} }} \over {\hat {r}}}

hvor impulsoperatoren virker som derivasjonsoperatoren ${\hat {\mathbf {p} }}=-i\hbar \partial /\partial {\hat {\mathbf {x} }}$ i en kommutator. Denne formelle ekvivalensen kan forenkle mange praktiske beregninger med disse kvantemekaniske variable.^[9]

Kvantisering av dreieimpuls

Når partikkelen har en impuls p, har den samtidig en dreieimpuls $\mathbf {L} =\mathbf {x} \times \mathbf {p}$ om origo. Kvantemekanisk gir det opphav til matrisene $\,{\hat {\mathbf {L} }}={\hat {\mathbf {x} }}\times {\hat {\mathbf {p} }}.$ Fra definisjonen av vektorproduktet kan man skrive de tre komponentene som ${\hat {L}}_{a}=\varepsilon _{abc}{\hat {x}}_{b}{\hat {p}}_{c}$ ved bruk av Levi-Civita-symbolet og summerer over de to like indeksene på høyre side.

Ved direkte utregning finner man kommutatoren $[{\hat {L}}_{a},{\hat {x}}_{b}]=i\hbar \,\varepsilon _{abc}{\hat {x}}_{c}$ og den tilsvarende $[{\hat {L}}_{a},{\hat {p}}_{b}]=i\hbar \,\varepsilon _{abc}{\hat {p}}_{c}$ som er typisk for kommutatoren med alle vektoroperatorer. Kombineres disse to uttrykkene, får man $[{\hat {L}}_{a},{\hat {L}}_{b}]=i\hbar \,\varepsilon _{abc}{\hat {L}}_{c}$ som alternativt kan skrives som

{\hat {\mathbf {L} }}\times {\hat {\mathbf {L} }}=i\hbar \,{\hat {\mathbf {L} }}.

Denne matematiske sammenhengen gir grunnlaget for all kvantisering av spinn hvor man med spinn mener ikke bare orbital dreieimpuls som er benyttet her, men alle sammenhenger hvor man har tre variable som oppfyller ${\hat {\mathbf {S} }}\times {\hat {\mathbf {S} }}=i\hbar \,{\hat {\mathbf {S} }}.$ Da slike spinnmatriser ikke kommuterer med hverandre, kan de ikke diagonaliseres samtidig. Men da kommutatoren mellom én av dem og det totale spinnet ${\hat {\mathbf {S} }}^{2}={\hat {S}}_{1}^{2}+{\hat {S}}_{2}^{2}+{\hat {S}}_{3}^{2}$ er null, kan egenverdiene til disse to bestemmes. Man finner da

{\hat {\mathbf {S} }}^{2}=s(s+1)\hbar ^{2}

hvor kvantetallet s kan ta verdiene 0, 1/2, 1, 3/2, 2 og så videre. Kvantemekanisk er derfor spinn alltid kvantisert og kan generelt ta halvtallige verdier. For vanlig, orbital dreieimpuls opptrer bare heltallige verdier.^[2]

For en partikkel i et sentralpotensial V(r) er det orbitale spinnet en bevart størrelse. Det følger fra kommutatoren

[{\hat {L}}_{a},{\hat {\mathbf {p} }}^{2}]=[{\hat {L}}_{a},{\hat {p}}_{b}{\hat {p}}_{b}]=i\hbar \,\varepsilon _{abc}({\hat {p}}_{b}{\hat {p}}_{c}+{\hat {p}}_{c}{\hat {p}}_{b})=0

da Levi-Civita-symbolet er antisymmetrisk i alle sine indekser. I tillegg er

[{\hat {L}}_{a},V({\hat {r}})]=\varepsilon _{abc}[{\hat {x}}_{b}\,{\hat {p}}_{c},V({\hat {r}})]=\varepsilon _{abc}{\hat {x}}_{b}[{\hat {p}}_{c},V({\hat {r}})]=-i\hbar \,\varepsilon _{abc}{{\hat {x}}_{b}{\hat {x}}_{c} \over {\hat {r}}}V'({\hat {r}})=0

av samme grunn. Dermed er kommutatoren med Hamilton-operatoren $[{\hat {\mathbf {L} }},{\hat {H}}]=0$ og den kvantiserte dreieimpulsen forblir konstant.

Vanlig vektoranalyse kan opplagt ikke uten videre benyttes for slike ikke-kommuterende variable. For eksempel finner man fra den fundamentale kommutatoren at

{\hat {\mathbf {x} }}\cdot ({\hat {\mathbf {p} }}\times {\hat {\mathbf {L} }})={\hat {\mathbf {L} }}^{2}\!,\;{\text{mens}}\;\;({\hat {\mathbf {p} }}\times {\hat {\mathbf {L} }})\cdot {\hat {\mathbf {x} }}={\hat {\mathbf {L} }}^{2}+2i\hbar \,{\hat {\mathbf {p} }}\cdot {\hat {\mathbf {x} }}

For en partikkel i et generelt potensial finnes det derfor ingen enkel måte å beregne de kvantemekaniske egenskapene i denne formuleringen av teorien.^[10]

Hydrogenatomet

Den nye kvantemekanikken ville ikke ble akseptert før den kunne forklare linjespektret til hydrogen minst like godt som i Bohrs atommodell. Allerede høsten 1925 lyktes Wolfgang Pauli med det ved å gjøre bruk av den spesielle Runge-Lenz-vektoren. Den opptrer i topartikkelsystem som blir holdt sammen av et Coulomb-potensial på formen V(r ) = -k/r hvor k er en konstant avhengig av de elektriske ladningene til partiklene. Hamilton-operatoren for hydrogenatomet er derfor

{\hat {H}}={{\hat {\mathbf {p} }}^{2} \over 2m}-{k \over {\hat {r}}}

På samme måte som den bevarte dreieimpulsen $\mathbf {L}$ blir en vektoroperator $\,{\hat {\mathbf {L} }},$ blir Runge-Lenz-vektoren $\mathbf {A}$ en tilsvarende vektoroperator ${\hat {\mathbf {A} }}.$ Den kan kvantiseres på lignende måte som dreieimpulsen ved å gjøre bruk av de nye kommutatorene $[{\hat {L}}_{a},{\hat {A}}_{b}]=i\hbar \,\varepsilon _{abc}{\hat {A}}_{c}$ og $[{\hat {A}}_{a},{\hat {A}}_{b}]=-2m{\hat {H}}i\hbar \,\varepsilon _{abc}{\hat {L}}_{c}.$ Energien til atomet kan dermed finnes fra sammenhengen

{\hat {\mathbf {A} }}^{2}=m^{2}k^{2}+2m{\hat {H}}({\hat {\mathbf {L} }}^{2}+\hbar ^{2})

som er den samme som i klassisk mekanikk når man ser bort fra det siste leddet med Plancks konstant. Dette gir de kvantiserte energinivåene

E=-{m \over 2\hbar ^{2}}{k^{2} \over (2j+1)^{2}}

hvor spinnkvantetallet j = 0, 1/2, 1, 3/2 og så videre. Med k = e²/4π ε₀ er dette i full overensstemmelse med Bohrs resultat der hovedkvantetallet n = 2j + 1 = 1, 2, 3 og så videre.^[11]

Omtrent samtidig med at Pauli gjennomførte denne beregningen, klarte også Dirac å utlede samme resultat for hydrogenatomet ved bruk av sin operatorformulering. Han gjorde ingen eksplisitt bruk av Runge-Lenz-vektoren, men forenklet i stedet problemet ved å beskrive den klassiske bevegelsen til elektronet i et plan. Kvantiseringen involverer dermed færre operatorer og kan igjen gjøres rent algebraisk.^[12]

Schrödingers bølgemekanikk

Erwin Schrödinger var professor ved Universitetet i Zürich da han høsten 1925 ga et kollokvium om de Broglies forslag om å beskrive partikler som materiebølger. Dette var basert på den duale beskrivelsen av lys som bølger og samtidig også som fotoner. Hvis det samme gjelder for en vanlig partikkel med energi E og impuls p, kan den derfor på denne måten tilordnes en frekvens ν = E/h og en bølgelengde λ = p/h der h er Plancks konstant. Etter kollokviet fikk Schrödinger den kommentaren at hvis dette var riktig, så måtte det også finnes en bølgeligning som beskriver partikkelen. Noen få uker senere hadde han utarbeidet en slik ligning. De første anvendelser av denne nye Schrödinger-ligningen og dens begrunnelse ble. publisert i flere artikler på begynnelsen av 1926. Løsning av ligningen tilsvarte en beregning av partikkelens eller systemets kvantetilstander som i Heisenbergs matrisemekanikk kun var antatt å finnes. Diskrete kvantefenomen kunne nå forklares ved en kontinuerlig «bølgemekanikk».^[1]

En bølge med en bestemt frekvens ν vil oppfylle Helmholtz-ligningen

(\nabla ^{2}+k^{2})\psi (\mathbf {r} )=0

hvor ψ er amplituden og k = 2π /λ er bølgetallet. Hvis denne skal beskrive en partikkel med masse m som beveger seg i et potensial V = V(r), er bølgelengden ifølge de Broglie gitt ved impulsen p. Denne finnes fra partikkelens totale energi E = p²/2m + V. På denne måten fant Schrødinger sin opprinnelige ligning

\nabla ^{2}\psi +{8\pi ^{2}m \over h^{2}}(E-V)\psi =0

Da den har lignende form som mange andre partielle differensialligninger som var kjente på den tiden, fantes det flere veletablerte metoder for hvordan den kunne løses. Allerede i sitt første arbeid viste Schrödinger hvordan den kunne anvendes på hydrogenatomet og gi kvantiserte verdier for energien E i overensstemmelse med Bohrs formel.^[8]

Operatorer og egenverdier

Den tidsuavhengige Schrödinger-ligningen kan skrives som

{\Big [}-{\hbar ^{2} \over 2m}{\boldsymbol {\nabla }}^{2}+V(\mathbf {r} ){\Big ]}\psi (\mathbf {r} )=E\psi (\mathbf {r} )

der nå den reduserte Planck-konstanten ħ = h/2π inngår. På venstre side kan man betrakte

{\hat {H}}=-{\hbar ^{2} \over 2m}{\boldsymbol {\nabla }}^{2}+V(\mathbf {r} )

som en «energioperator» som. virker på en bølgefunksjon ψ(r). Den fremkommer fra den klassiske Hamilton-funksjonen og omtales derfor som Hamilton-operatoren. Da tar ligningen formen ${\hat {H}}\psi =E\psi ,$ og de tillatte energiene sies å være egenverdier til denne operatoren. De tilsvarende bølgefunksjonene er operatorens egenfunksjoner. I dette tilfellet gir disse funksjonene en matematisk beskrivelse av kvantetilstander med bestemt energi.^[2]

Ved å definere en «impulsoperator» som ${\hat {\mathbf {p} }}=-i\hbar {\boldsymbol {\nabla }}$ med komponenter ${\hat {p}}_{a}=-i\hbar {\partial \over \partial x_{a}},$ kan Hamilton-operatoren i dette tilfellet skrives som

{\hat {H}}={{\hat {\mathbf {p} }}^{2} \over 2m}+V(\mathbf {r} )

Det gjør det mulig å finne denne direkte fra det klassiske uttrykket for energien til partikkelen hvor den kinetiske delen uttrykkes ved partikkelens impuls.

I denne bølgemekanikken vil en partikkel med en bestemt impuls p beskrives av en bølgefunksjon som er en egenfunksjon av impulsoperatoren. Den må derfor tilfredsstille ${\hat {\mathbf {p} }}\psi =\mathbf {p} \psi$ og er derfor gitt ved den enkle differensialligningen

-i\hbar {\boldsymbol {\nabla }}\psi _{\mathbf {p} }(\mathbf {r} )=\mathbf {p} \,\psi _{\mathbf {p} }(\mathbf {r} )

Den har som løsning $\psi _{\mathbf {p} }(\mathbf {r} )=Ae^{i\mathbf {p} \cdot \mathbf {r} /\hbar }$ hvor A er en konstant. Bølgefunksjonen for en partikkel med bestemt impuls er derfor en kompleks funksjon. Den inneholder ingen informasjon om partikkelens posisjon i overensstemmelse med Heisenbergs uskarphetsrelasjon. Men funksjonen er vanligvis ikke en egenfunksjon for Hamilton-operatoren. Det er tilfelle kun for frie partikler hvor potensialet V = 0. En bunden partikkel har ikke noen veldefinert impuls, men vil likevel ha bestemte energier. Dette kan lett illustreres ved å betrakte løsninger av Schrödinger-ligningen i enkle, 1-dimensjonale eksempel.^[13]

Kanoniske kommutatorer

Impulsoperatoren ${\hat {\mathbf {p} }}=-i\hbar {\boldsymbol {\nabla }}$ virker på alle funksjoner som står på den høyre siden av den som ved vanlig derivasjon. Da er for eksempel

{\partial  \over \partial x}xf(x)=f(x)+x{\partial  \over \partial x}f(x)

som kan skrives på den litt mer abstrakt formen

{\partial  \over \partial x}x-x{\partial  \over \partial x}=1

En videreføring av denne skrivemåten er å tenke seg en «enhetsoperator» som kan virke på enhver funksjon og gir samme funksjon tilbake som resultat. Likedan kan man tenke seg en «posisjonsoperator» ${\hat {x}}$ som virker på en funksjon f (x ) og gir dermed xf (x ) tilbake. For impulsoperatoren i x-retning gjelder derfor sammenhengen $[{\hat {x}},{\hat {p}}]=i\hbar$ hvor kommutatoren av to operatorer er definert som $[{\hat {a}},{\hat {b}}]={\hat {a}}{\hat {b}}-{\hat {b}}{\hat {a}}.$

Med en ekstra koordinat y vil nå samme betraktning gi $[{\hat {y}},{\hat {p}}_{x}]=[{\hat {x}},{\hat {p}}_{y}]=0.$ Da rekkefølgen av to partielle derivasjoner ∂_x = ∂ /∂x og ∂_y = ∂ /∂y fritt kan byttes om, vil på lignende vis kommutatoren $[{\hat {p}}_{x},{\hat {p}}_{y}]=0.$ Avgjørende for all kvantisering er de kanoniske kommutatorene

[{\hat {x}}_{a},{\hat {p}}_{b}]=i\hbar \,\delta _{ab}

hvor Kronecker-delta på høyre side er null hvis indeksene er forskjellige og lik med én når de er like.^[2]

Når partikkelens impuls er gitt ved virkningen av en operator, vil også dens dreieimpuls $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ beskrives av en vektoroperator med komponenter

{\begin{aligned}{\hat {L}}_{x}&=-i\hbar (y\partial _{z}-z\partial _{y}),\;\;{\hat {L}}_{y}=-i\hbar (z\partial _{x}-x\partial _{z}),\\{\hat {L}}_{z}&=-i\hbar (x\partial _{y}-y\partial _{x}).\end{aligned}}

De kommuterer ikke seg imellom, men oppfyller den kanoniske kommutatoren

[{\hat {L}}_{x},{\hat {L}}_{y}]=i\hbar {\hat {L}}_{z}

pluss de to andre som fremkommer ved syklisk ombytte av operatorene. Egenverdiene til kun én av dem kan derfor bestemmes. Vanligvis velges den å være dreieimpulsen om z-aksen. Ved direkte utregning finner man at $[{\hat {L}}_{z},{\hat {\mathbf {L} }}^{2}]=0$ slik at også egenverdiene til den totale dreieimpulsen ${\hat {\mathbf {L} }}^{2}={\hat {L}}_{x}^{2}+{\hat {L}}_{y}^{2}+{\hat {L}}_{z}^{2}$ kan finnes. Dette er helt i overensstemmelse med hva som ble funnet fra Heisenbergs matrisemekanikk noen få måneder tidligere og leder til den nå vanlige kvantisering av dreieimpuls.

Sentralsymmetrisk potensial

Når en partikkel beveger seg i et potensial V(r ) som bare avhenger av avstanden r til et sentrum, er det rotasjonssymmetrisk om dette punktet. Det er derfor naturlig å benytte kulekoordinater (r, θ, φ) istedenfor kartesiske koordinater (x, y, z) i Schrödinger-ligningen. Ved å bruke den klassiske identiteten $(\mathbf {r} \times \mathbf {p} )^{2}=r^{2}p^{2}-(\mathbf {r} \cdot \mathbf {p} )^{2},$ kan man i den kinetiske energien benytte at

\mathbf {p} ^{2}=p_{r}^{2}+{1 \over r^{2}}\mathbf {L} ^{2}

hvor den radielle komponenten er $p_{r}=(\mathbf {r} \cdot \mathbf {p} )/r.$ Kvantemekanisk blir den en operator som kan finnes fra sammenhengen ${\hat {\mathbf {p} }}^{2}=-\hbar ^{2}\nabla ^{2}$ og uttrykket for Laplace-operatoren i kulekoordinater. Det gir

{\hat {p}}_{r}^{2}=-{\hbar ^{2} \over r^{2}}{\partial  \over \partial r}\left(r^{2}{\partial  \over \partial r}\right)=-\hbar ^{2}\left({\partial ^{2} \over \partial r^{2}}+{2 \over r}{\partial  \over \partial r}\right)

samt operatoren som bestemmer den totale dreieimpulsen

{\hat {\mathbf {L} }}^{2}=-\hbar ^{2}\left[{1 \over \sin \theta }{\partial  \over \partial \theta }\left(\sin \theta {\partial  \over \partial \theta }\right)+{1 \over \sin ^{2}\theta }{\partial ^{2} \over \partial \phi ^{2}}\right]

Ved kvantisering finner man dens egenfunksjoner som er sfærisk harmoniske funksjoner Y_ℓm(θ,φ). Egenverdiene følger fra

{\hat {\mathbf {L} }}^{2}Y_{\ell m}(\theta ,\phi )=\hbar ^{2}\ell (\ell +1)Y_{\ell m}(\theta ,\phi )

hvor kvantetallet ℓ = 0, 1, 2, 3 og så videre. Heltallet m ligger i intervallet - ℓ ≤ m ≤ ℓ og tar derfor 2ℓ + 1 forskjellige verdier. Energien til partikkelen blir uavhengig av dette «magnetiske kvantetallet».^[13]

Schrödinger-ligningen kan nå forenkles ved å skrive den fulle bølgefunksjonen som

\psi (\mathbf {r} )=R(r)Y_{\ell m}(\theta ,\phi )

Den radielle delen av denne funksjonen må derfor være en løsning av den ordinære differensialligningen

\left[-{\hbar ^{2} \over 2m}\left({d^{2} \over dr^{2}}+{2 \over r}{d \over dr}\right)+{\ell (\ell +1)\hbar ^{2} \over 2mr^{2}}+V(r)\right]R(r)=ER(r).

En videre forenkling kan gjøres ved å innføre funksjonen u(r) = r R(r), Det sentralsymmetriske egenverdiproblemet blir da redusert til å finne løsninger av ligningen

-{\hbar ^{2} \over 2m}{d^{2}u \over dr^{2}}+V_{eff}(r)u(r)=Eu(r)

hvor det effektive potensialet er

V_{eff}(r)=V(r)+{\ell (\ell +1)\hbar ^{2} \over 2mr^{2}}

Det siste leddet skyldes dreieimpulsen til partikkelen og virker som en sentrifugalkraft som holder den borte fra origo i r = 0. I nærheten av dette punktet dominerer leddet og betyr at den radielle funksjonen varierer som u(r) ≈ r^ℓ+1 i dette området.^[14]

Allerede i sitt første arbeid kunne Schrödinger løse denne radielle ligningen for Coulomb-potensialet som opptrer i hydrogenatomet. Dette gjorde det klart at denne bølgemekaniske formuleringen av kvantefysikken kunne anvendes i langt større grad enn den abstrakte matrisemekanikken til Heisenberg.

Eksempel: Sfærisk kassepotensial

En bundet partikkel i et atom for eksempel befinner seg per definisjon i et endelig område av rommet. Den må derfor kvanemeaknisk beskrives av en bølgefunksjon som går mot null ved store avstander. Den enkleste illustrasjon av en slik situasjon er en partikkel som kun kan bevege seg i én dimensjon mens den befinner seg i et uendelig dypt kassepotensial. Mer realistisk er å anta at partikkelen kan bevege seg fritt i alle tre dimensjoner innenfor en avstand r < a fra origo hvor a er radius til et uendelig dypt kassepotensialet.

Inne i kassen hvor potensialet V(r) = 0, er de radielle bølgefunksjonene med dreieimpuls ℓ = 0 enklest å finne. Differensialligningen for disse s-tilstandene er

{d^{2}u_{0} \over dr^{2}}+k^{2}u_{0}(r)=0

hvor størrelsen k bestemmer partiklens energi ved sammenhengen E = ħ²k²/2m. Den er bestemt ved kravet at bølgefunksjonen må være null utenfor kassen. Da den samtidig må være kontinuerlig gjennom dens overflate r = a, må u₀(ka) = 0. Denne grensebvtingelsen gir nå den entydige løsningen

u_{0}(r)=\sin kr

med de kvantiserte verdiene k = n π /a. Dermed har s-tilstandene energiene

E_{0n}={\hbar ^{2} \over 2ma^{2}}(\pi n)^{2}

hvor n = 1, 2, 3 etc virker som et radielt kvantetall. Tilstandene kan betegnes som 1s, 2s og så videre. Dette er samme resultat som for løsningen i et éndimensjonalt kassepotensial med samme utstrekning.^[13]

Funksjonen R₀(r) = u₀/r er den sfæriske Bessel-funksjonen j₀(kr) av laveste orden. Løsning av Schrödinger-ligning for ℓ > 0 er på tilsvarende vis gitt ved mer kompliserte Bessel-funksjoner j_ℓ(kr). Energiene til disse tilstanden må dermed tilfredsstille grensebetingelsen j_ℓ(ka) = 0. Det betyr at k = x_ℓn /a hvor x_ℓn er n-te nullpunkt til Bessel-funksjonen j_ℓ(x), De kvantiserte energiene for partikkelen i dette potensialet er derfor

E_{\ell n}={\hbar ^{2} \over 2ma^{2}}x_{\ell n}^{2}

For de laveste p-tilstandene med ℓ = 1 er nullpunktene x₁₁ = 4.49 og x₁₂ = 7.73. Derfor har 1p-tilstanden en energi mellom 1s og 2s, mens 2p ligger over 2s. På tilsvarende vis betyr x₂₁ = 5.76 og x₃₁ = 6.99 at tilstanden 1d med ℓ = 2 ligger like under 2s-tilstanden, mens 1f ligger like over denne.^[14]

Når det sfæriske kassepotensialet modifiseres til et tredimensjonalt, harmonisk oscillatorpotensial V(r) = mω²r²/2, kan de kvantiserte energiene beregnes eksakt. De blir

E_{\ell n_{r}}=\hbar \omega (2n_{r}+\ell +3/2)

hvor n_r = 0, 1, 2, ... er et radielt kvantetall. Energinivåene er bestemt av kombinasjonen n = 2n_r + ℓ og vil derfor generelt være degenererte. Det gjelder ikke for grunntilstanden med energi 3ħω/2 og kvantetall ℓ = n_r = 0. Likedan består det første, eksisterte energinivå 5ħω/2 entydig av tilstanden ℓ = 1, n_r = 0. Derimot inneholder nivået 7ħω/2 både tilstanden ℓ = 2, n_r = 0 og ℓ = 0, n_r = 1. Denne degenerasjonen av energinivåene stemmer overens med hva som finnes ved å løse Schrödinger-ligningen for dette potensialet ved bruk av kartesiske koordinater. Det skyldes at det mekaniske systemet har en ekstra symmetri ut over rotasjonssymmetrien som allerede er benyttet ved løsningen. Noe tilsvarende gjelder også for Coulomb-potensialet som har en bevart Runge-Lenz-vektor.

Interpretasjon av bølgefunksjon

Da Schrödinger lanserte sin bølgemekanikk i 1926, mente han at bølgefunksjonen ψ(r) for et elektron i et atom var et uttrykk for hvordan dets ladning var fordelt inni atomet. Mer nøyaktig, hvis e er elektronets ladning, så er e |ψ |² den elektriske ladningstettheten i atomet. Det bundne elektronet kunne ikke beskrives som en enkel bølge, men måtte i stedet betraktes som en «bølgepakke» sammensatt av mange bølger. Denne beskrivelsen eller mentale bilde av bølgefunksjonen møtte motstand fra flere hold. Ikke uventet var Heisenberg meget kritisk.^[2]

Det ble snart klart at å betrakte bølgefunksjonen som en bølge i klassisk fysikk var villedende. For eksempel hvis man betrakter Schrödinger-ligningen for to partikler,

{\Big [}{{\hat {\mathbf {p} }}_{1}^{2} \over 2m_{1}}+{{\hat {\mathbf {p} }}_{2}^{2} \over 2m_{2}}+V(\mathbf {r} _{1},\mathbf {r} _{2}){\Big ]}\psi (\mathbf {r} _{1},\mathbf {r} _{2})=E\psi (\mathbf {r} _{1},\mathbf {r} _{2})

så beskriver ikke funksjonen $\psi (\mathbf {r} _{1},\mathbf {r} _{2})$ noen bølge i det tredimensjonale rommet eller to bølger som følger hver av partiklene i dette rommet. I alminnelighet kan man kun si at det er en kompleks funksjon i et seksdimensjonalt rom.

Eksperimentene til Davisson, Germer og George Thomson viste at ett elektron hadde bølgeegenskaper under krystalldiffraksjon. Men dette interferensfenomenet var vanskelig å kombinere med bildet av et elektron som en partikkel hvis elektriske ladning skulle splittes opp på denne måten.

Den interpretasjon av bølgefunksjonen som er blitt stående, kom Max Born med allerede i 1926. Den var inspirert av Einstein som hadde foreslått at en klassisk, elektromagnetisk bølge kunne betraktes som en «pilotbølge» som styrte et foton. Ut fra denne analogien mente Born at den kvantemekaniske bølgefunksjonen $\psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots )$ kan betraktes som en «sannsynlighetsamplitude» i. den forstand at det absolutte kvadrat

P(\mathbf {r} _{1},\mathbf {r} _{2},\ldots )=\psi ^{*}(\mathbf {r} _{1},\mathbf {r} _{2},\ldots )\psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots )

er proporsjonal med sannsynligheten for å finne den første partikkelen i posisjon r₁, den andre i punktet r₂ og så videre.^[8]

For én partikkel som.benyttes for eksempel i et dobbeltspalteeksperiment, vil bølgefunksjon bli en superposisjon $\psi _{1}(\mathbf {r} )+\psi _{2}(\mathbf {r} )$ . Sannsynligheten for å detektere partikkelen bak spalten blir da

{\begin{aligned}P(\mathbf {r} )&=|\psi _{1}(\mathbf {r} )+\psi _{2}(\mathbf {r} )|^{2}\\&=|\psi _{1}(\mathbf {r} )|^{2}+|\psi _{2}(\mathbf {r} )|^{2}+\psi _{1}^{*}(\mathbf {r} )\psi _{2}(\mathbf {r} )+\psi _{2}^{*}(\mathbf {r} )\psi _{1}(\mathbf {r} )\end{aligned}}

hvor de to siste leddene gir den kvantemekaniske bølgeinterferensen. Selv om partikkelen beskrives som en bølge som strekker seg over hele rommet, vil den bak spalten kun detekteres i diskrete punkt r og må derfor oppfattes som en partikkel. Man kan ikke forutsi i hvilket punkt dette vil skje, bare sannsynligheten for at en slik observasjon kan gjøres.

Et annet, viktig spørsmål er hvor man skal sette grensen mellom klassisk fysikk og fenomener som må beskrives kvantemekanisk. Hvis man antar at også makroskopiske system som en innestengt katt i en kasse, kan befinne seg i forskjellige kvantetilstander og superposisjoner av slike, blir man konfrontert med grunnleggende paradokser som ennå ikke er helt avklart. Et godt eksempel på et slikt system er Schrödingers katt. Spesielt i mer populær litteratur blir slike problemstillinger den dag i dag mye diskutert.^[15]

Tidsavhengig Schrödinger-ligning

Hvordan et kvantesystem forandrer seg med tiden, ble først undersøkt av Schrödinger i ett senere arbeid. Det kan ikke da lenger ha en konstant energi og vil i stedet kunne gå fra en stasjonær tilstand til en annen. På den måten vil en tidsavhengig beskrivelse kunne forklare kvanteoverganger som for eksempel når et atom plutselig sender ut et foton.

I en stasjonær tilstand har systemet en bestemt energi E og kan beskrives ved en egenfunksjon av den tidsuavhengige ligningen ${\hat {H}}\psi =E\psi .$ Denne bølgefunksjonen har samtidig en frekvens ω = E/ħ og vil ha en tidsavhengighet som må være på formen $\exp(-i\omega t).$ Den stasjonære Schrödinger-ligningen kan derfor skrives på den ekvivalente formen

{H}({\hat {\mathbf {p} }},\mathbf {r} )\Psi (\mathbf {r} ,t)=i\hbar {\partial  \over \partial t}\Psi (\mathbf {r} ,t)

når den tidsavhengig bølgefunksjonen skrives som $\Psi (\mathbf {r} ,t)=\psi (\mathbf {r} )e^{-iEt/\hbar }.$ Denne formen av ligningen er det nå naturlig å benytte for et kvantesystem som er i en vilkårlig tilstand og ikke nødvendigvis i en egentilstand av Hamilton-operatoren. Den kalles derfor for den tidsavhengige Schrödinger-ligningen.^[13]

Dens innhold kan illustreres ved å betrakte et system som ved tiden t = 0 er i en superposisjon av to tilstander. De betegnes som $\psi _{1}(\mathbf {r} )$ og $\psi _{2}(\mathbf {r} )$ og begge antas å være egentilstander av Hamilton-operatoren med energier henholdsvis E₁ og E₂. I utgangspunktet er systemet da i tilstanden

\Psi (\mathbf {r} ,t=0)=C_{1}\psi _{1}(\mathbf {r} )+C_{2}\psi _{2}(\mathbf {r} )

hvor C_1,2 er konstanter som bestemmer sannsynlighetene for at systemet er i den første eller andre tilstanden ved tiden t = 0. Denne superposisjonen er ikke en egentistand av Hamilton-operatoren. Systemets videre utvikling med tiden er likevel gitt som

\Psi (\mathbf {r} ,t>0)=C_{1}\psi _{1}(\mathbf {r} )e^{-iE_{1}t/\hbar }+C_{2}\psi _{2}(\mathbf {r} )e^{-iE_{2}t/\hbar }

og vises direkte ved derivasjon å oppfylle den tidsavhengige Schrödinger-ligningen. Sannsynligheten for å finne partikkelen i et bestemt punkt vil nå variere med tiden. I dette tilfellet vil det utgjøre en oscillasjon med frekvens (E₁ - E₂)/ħ som oppstår fra produktet mellom de to leddene i funksjonen.

Den tidsavhengige Schrödinger-ligningen har samme form som differensialligningen som definerer eksponentialfunksjonen. Derfor kan også tidsutviklingen finnes mer direkte fra

{\begin{aligned}\Psi (t)&=e^{-i{\hat {H}}t/\hbar }\Psi (0)\\&=\left[1+\left(-{it \over \hbar }{\hat {H}}\right)+{1 \over 2!}\left(-{it \over \hbar }{\hat {H}}\right)^{2}+\cdots \right]\Psi (0)\end{aligned}}

så lenge Hamilton-operatoren er uavhengig av tiden. Det vil ikke være tilfelle hvis for eksemel den inneholder et potensial som varierer med tiden. En slik situasjon har man for et atom som vekselvirker med lys. Da kan tidsutviklingen vanligvis kun beregnes med perturbasjonsteori.

I kvantemekanikken har den tidsavhengige Schrödinger-ligningen en helt sentral betydning. Dens form er uavhengig av om den beskriver én eller mange partikler, om disse er ikke-relativistiske eller relativistiske eller om Hamilton-operatoren er eksplisitt tidsavhengig eller ikke. Uansett system har den alltid den samme form

i\hbar {\partial  \over \partial t}\Psi (t)={\hat {H}}\Psi (t)

hvor de detaljerte egenskapene til systemet opptrer i Hamilton-operatoren ${\hat {H}}.$ Denne generelle gyldighet holder ikke bare for systemer bestående av partikler, men også for kvanteelektrodynamikk og andre kvantefeltteorier.^[10]

Dirac-formalisme

Heisenbergs matrisemekanikk og Schrödingers bølgemekanikk viste seg snart å være to forskjellige, men ekvivalente fremstillinger av samme kvantemekanikk. Dette kan enklest vises ved bruk av bra-ket-notasjonen som ble utviklet av Paul Dirac og basert på lineær algebra i et Hilbert-rom. En kvantetilstand er en «ket-vektor» $|\Psi \rangle$ i dette rommet. Den duale eller adjungerte vektor $\langle \Psi |$ kalles en «bra-vektor» og inngår i et reelt indreprodukt $\langle \Psi |\Psi \rangle >0.$ For to forskjellige vektorer $|\Psi _{i}\rangle$ og $|\Psi _{j}\rangle$ er det definert slik at $\langle \Psi _{i}|\Psi _{j}\rangle =\langle \Psi _{j}|\Psi _{i}\rangle ^{*}.$ Er produktet lik null, sies vektorene å være «ortogonale» i forhold til hverandre.^[16]

For et kvantesystem med et N-dimensjonalt Hilbert-rom ${\cal {{H}_{N}}}$ kan det introduseres et basissystem $|1\rangle ,|2\rangle ,\ldots ,|N\rangle$ slik at hver vektor kan skrives som

|\Psi \rangle =\sum _{n=1}^{N}\psi _{n}|n\rangle

hvor de komplekse tallene $\psi _{n}$ er vektorens komponenter. Basisvektorene er lineært uavhengige av hverandre og utgjør et «fullstendig sett» av vektorer. De er ortogonale til hverandre, og det er mest hensiktsmessig å velge dem med samme lengde eller norm. Da er $\langle m|n\rangle =\delta _{mn}$ hvor Kronecker-deltaet på høyre side er null for forskjellige vektorer og én når indeksene er de samme. Man har da en «ortonormert» basis.

Komponentene til en vektor $|\Psi \rangle$ er nå gitt som $\psi _{n}=\langle n|\Psi \rangle .$ Det indre produkt mellom denne vektoren og en annen vektor $|\Phi \rangle$ med komponenter $\phi _{n}=\langle n|\Phi \rangle$ blir dermed

\langle \Psi |\Phi \rangle =\sum _{n=1}^{N}\psi _{n}^{*}\phi _{n}

og kan ta hvilken som helst verdi. Det omtales også ofte som projeksjonen av den ene vektoren på den andre.^[13]

Operatorer og hermitisitet

Uttrykket for en generell vektor kan omformes til

|\Psi \rangle =\sum _{n}\psi _{n}|n\rangle =\sum _{n}|n\rangle \langle n|\Psi \rangle

Det er derfor naturlig å betrakte summen

{\hat {I}}=\sum _{n}|n\rangle \langle n|

med produkter av vektorene i et fullstendig sett som en «identitetsoperator». Den kan virke på hvilken som helst vektor og dermed gi nøyaktig den samme vektoren. Vanligvis settes den derfor ganske enkelt lik med ${\hat {I}}=1.$ En generell operator kan skrives på formen

{\hat {A}}=\sum _{m,n}A_{mn}|m\rangle \langle n|

og vil I alminnelighet resultere i en annen vektor $|\Psi '\rangle$ i det samme Hilbert-rommet. Det følger fra

{\begin{aligned}{\hat {A}}|\Psi \rangle &=\sum _{m,n}A_{mn}|m\rangle \langle n|\Psi \rangle =\sum _{m,n}A_{mn}\psi _{n}|m\rangle \\&=|\Psi '\rangle =\sum _{m}\psi '_{m}|m\rangle \end{aligned}}

der den nye vektoren har de transformerte komponentene $\psi '_{m}=\sum _{n}A_{mn}\psi _{n}.$ Produktet av to operatorer er vanligvis avhengig av deres rekkefølge. Dette uttrykkes ved deres kommutator

[{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}

som i alminnelighet er en ny operator. Den inverse ${\hat {A}}^{-1}$ av en operator ${\hat {A}}$ er definert ved at ${\hat {A}}{\hat {A}}^{-1}={\hat {A}}^{-1}{\hat {A}}={\hat {I}}.$ Derfor er den inverse av et produkt gitt ved produktet av de inverse i motsatt rekkefølge da

({\hat {A}}{\hat {B}})^{-1}{\hat {A}}{\hat {B}}={\hat {B}}^{-1}{\hat {A}}^{-1}{\hat {A}}{\hat {B}}={\hat {B}}^{-1}{\hat {B}}={\hat {I}}.

De komplekse koeffisientene $A_{mn}=\langle m|{\hat {A}}|n\rangle$ utgjør komponentene til operatoren ${\hat {A}}.$ Tilsammen utgjør de en $N\times N$ matrise. Den hermitisk adjungerte matrisen $A^{\dagger }$ med element $A_{mn}^{\dagger }=A_{nm}^{*}$ definerer en hermitisk adjungert operator ${\hat {A}}^{\dagger }.$ Den har derfor den viktige egenskapen

\langle \Phi |{\hat {A}}|\Psi \rangle ^{*}=\langle \Psi |{\hat {A}}^{\dagger }|\Phi \rangle

Hermitisk adjungering er en utvidelse av vanlig, kompleks konjugasjon. Operasjonen kan også virke på en ket-vektor og gi den tilsvarende bra-vektor eller omvendt. Mer generelt gjelder

({\hat {A}}|\Psi \rangle )^{\dagger }=\langle \Psi |{\hat {A}}^{\dagger }

En operator som er lik sin hermitisk adjungerte, sies å være «selvadjungert» eller ganske enkelt hermitisk. De spiller en sentral rolle i kvantemekanikken.^[17]

Egenvektorer og egenverdier

Når en operator ${\hat {A}}$ virker på en tilstand eller vektor $|\Psi \rangle$ og resultatet er en vektor i samme retning slik at

{\hat {A}}|\Psi \rangle =a|\Psi \rangle ,

sies vektoren å være en egenvektor til denne operatoren. Tallet a vil i alminnelighet være komplekst og kalles en egenverdi til operatoren. Men i det tilfellet at operatoren er hermitisk, er egenverdien et reelt tall. Det følger fra en multiplikasjon med den adjungerte brå-vektoren $\langle \Psi |$ fra venstre som gir $\langle \Psi |{\hat {A}}|\Psi \rangle =a\langle \Psi |\Psi \rangle .$ Begge de to indreproduktene her er nå reelle og derfor er også egenverdien a reell.

En operator kan generelt ha flere forskjellige egenverdier. De tilsvarende egenvektorene vil da være ortogonale. Det følger fra de to egenverdiligningene

{\hat {A}}|\Psi _{m}\rangle =a_{m}|\Psi _{m}\rangle ,\;\;\;{\hat {A}}|\Psi _{n}\rangle =a_{n}|\Psi _{n}\rangle

Her kan den første ligningen multipliseres med $\langle \Psi _{n}|$ fra venstre. Når man så benytter samtidig den andre ligningen på formen $\langle \Psi _{n}|{\hat {A}}=a_{n}\langle \Psi _{n}|,$ ser man at $(a_{m}-a_{n})\langle \Psi _{n}|\Psi _{m}\rangle =0.$ Hvis de to egenverdiene er forskjellige, må derfor indreproduktet av de tilsvarende egenvektorene være lik med null.^[17]

På lignende måte er det lett å vise at hvis en vektor $|\Psi \rangle$ er samtidig egenvektor til to forskjellige operatorer ${\hat {A}}$ og ${\hat {B}},$ må disse operatorene kommutere med hverandre, det vil si $[{\hat {A}},{\hat {B}}]=0.$ En egentilstand kan derfor karakteriseres ved egenverdiene til alle operatorer som kommuterer med hverandre. Hvis derimot de to operatorene ikke kommuterer med hverandre, kan de ikke måles eller bestemmes samtidig. Gjøres det, vil resultatet være beheftet med en usikkerhet som matematisk kan uttrykkes ved Heisenbergs uskarphetsrelasjon.

Et grunnleggende teorem i lineær algebra er at alle egenvektorene til en hermitisk operator utgjør et «fullstendig sett». Det betyr at de kan benyttes som basisvektorer i det tilsvarende Hilbert-rommet. Hver slik operator gir derfor et gangspunkt for å konstruere en tilsvarende basis i dette rommet. Det muliggjør også transformasjoner mellom matriserepresentasjoner av operatorer i forskjellige basissystem.

Kvantemekanikkens postulater

Klassisk mekanikk er basert på forskjellige lover. De kan være utformet på forskjellig vis, men beskriver de samme fysiske fenomen. Eksempel på slike ulike formuleringer kan være Newtons bevegelseslover eller Hamiltons virkningsprinsipp.

På samme måte er kvantemekanikk basert på noen få antagelser.^[17] Disse kan summeres opp i tre grunnleggende postulat:

For hver observerbar størrelse A eller obervabel finnes det en tilsvarende, hermitisk operator ${\hat {A}}.$ En måling av denne størrelsen vil gi en av operatorens egenverdier. Den viktigste operatoren er Hamilton-operatoren ${\hat {H}}$ hvis egenverdier er systemets mulige energier.
Resultatet av en måling av en eller flere observable til et kvantesystem ved tiden t er kodet inn i en tilstandsvektor $|\Psi \rangle =|\Psi ,t\rangle$ i Hilbert-rommet for systemet. Så lenge vektoren ikke er en egentilstand av den observable ${\hat {A}},$ vil en måling av denne gi et midlere resultat $\langle {\hat {A}}\rangle =\langle \Psi |{\hat {A}}|\Psi \rangle$ når tilstanden er normert som $\langle \Psi |\Psi \rangle =1.$
Tilstandsvektoren til systemet forandrer seg med tiden ifølge den tidsavhengige Schrödinger-ligningen

\;\;\;\;\;\;\;\;\;\;\;\;i\hbar {\partial  \over \partial t}|\Psi ,t\rangle ={\hat {H}}|\Psi ,t\rangle

Størrelsen til alle resulterende kvanteeffekter er bestemt av den reduserte Planck-konstanten ħ = h/2π som Dirac innførte.

Observasjon og målinger

Begrepene oberservasjon og måling av en observabel ${\hat {A}}$ brukes ofte om hverandre. Ved én enkelt måling tilordnes en verdi til denne størrelsen som er en av operatorens egenverdier $a_{m}$ bestemt ved egenverdiligningen ${\hat {A}}|m\rangle =a_{m}|m\rangle .$ Dette representerer en observasjon og betyr i praksis en forandring i en makroskopisk, klassisk størrelse som kan registrere og lagre verdien. Direkte etter observasjonen befinner kvantesystemet seg i egentilstanden $|n\rangle$ og vil videre utvikle seg med tiden på en deterministisk måte gitt ved Schrödinger-ligningen.^[10]

På et senere tidspunkt befinner systemet seg i en ny tilstand $|\Psi \rangle$ som i alminnelighet ikke er noen egentilstand til den samme operatoren. En ny måling vil derfor kanskje gi en annen egenverdi. Men operatorens egenvektorer danner et fullstendig sett slik at man generelt har $|\Psi \rangle =\sum _{n}\psi _{n}|n\rangle$ med $\psi _{n}=\langle n|\Psi \rangle .$ Da vil

\langle \Psi |{\hat {A}}|\Psi \rangle =\sum _{n}\psi _{n}\langle \Psi |{\hat {A}}|n\rangle =\sum _{n}a_{n}|\psi _{n}|^{2}

Hvis man nå benytter normeringen $\langle \Psi |\Psi \rangle =1$ som betyr at

\sum _{n}|\psi _{n}|^{2}=1,

kan man betrakte $P_{n}=|\psi _{n}|^{2}$ som sannsynligheten for at systemet $|\Psi \rangle$ er i egentilstanden $|n\rangle .$ Av denne grunn kalles det komplekse tallet $\psi _{n}=\langle n|\Psi \rangle$ for sannsynlighetsamplituden for at dette skal være tilfelle. Uttrykket $\langle \Psi |{\hat {A}}|\Psi \rangle$ gir derfor den midlere verdi for den observable ${\hat {A}}$ når systemet er i en vilkårlig tilstand $|\Psi \rangle .$ Den kalles også for forventningsverdien.^[16]

En måling av denne midlere verdien er ganske omstendelig. Mens hver enkeltmåling gir en egenverdi, vil forventningsverdien kreve at man disponerer over et stort antall identiske system som tilberedes i eksakt samme tilstand. Den midlere verdien av et stort antall målinger av samme observabel på disse systemene, som hver for seg gir en egenverdi, vil da gi dens forventningsverdi $\langle {\hat {A}}\rangle$ utregnet som i vanlig sannsynlighetsregning.

Tidsutvikling og Heisenberg-bilde

For et stasjonært system er Hamilton-operatoren uavhengig av tiden. Den tidsavhengige Schrödinger-ligningen kan da integreres direkte til å gi tilstandsvektoren ved et senere tidspunkt. Resultatet kan skrives som $|\Psi ,t\rangle ={\hat {U}}(t)|\Psi ,0\rangle$ hvor

{\hat {U}}(t)=e^{-i{\hat {H}}t/\hbar }

er «tidsutviklingsoperatoren». Mens denne bringer systemet fremover i tid, vil den inverse operatoren

{\hat {U}}^{-1}(t)={\hat {U}}(-t)=e^{i{\hat {H}}t/\hbar }

bringe det bakover i tid. Da Hamilton-operatoren er hermitisk, vil dette også være lik med den adjungerte operatoren ${\hat {U}}^{\dagger }(t).$ Det betyr at den oppfyller ${\hat {U}}^{\dagger }{\hat {U}}={\hat {U}}{\hat {U}}^{\dagger }={\hat {I}}.$ En slik operator sies å være unitær. For tidsutviklingsoperatoren betyr det rent fysisk at systemet vil forbli i en eller annen kvantetilstand i det samme Hilbert-rommet.^[18]

Hvis man betrakter et veldig kort tidsrom τ , så vil ikke systemet forandres så mye. Tidsutviklingsoperatoren kan da skrives som

{\hat {U}}(\tau )={\hat {I}}-{i \over \hbar }{\hat {H}}\tau +\cdots

Fra denne sammenhengen ser man at Hamilton-operatoren får systemet til å forandre seg i korte øyeblikk eller at den er en generator for slike forandringer. En endelig forandring over en tid t = nτ kan så bygges opp av n små transformasjoner etterfulgt av hverandre eller ${\hat {U}}(t)={\hat {U}}(\tau ){\hat {U}}(\tau )\cdots {\hat {U}}(\tau ).$ I grensen hvor τ blir tilstrekkelig liten har man da

{\hat {U}}(t)=\left({\hat {I}}-{i \over \hbar }{\hat {H}}{t \over n}\right)^{n}=e^{-i{\hat {H}}t/\hbar }

ut fra definisjonen av eksponentialfunksjonen i grensen der n blir veldig stor.

Denne fremstilling av tidsutviklingen er gjort i det som kalles «Schrödinger-bildet». Den skyldes at tilstandsvektoren for systemet varierer med tiden. Forventningsverdien av en operator

\langle {\hat {A}}\rangle (t)=\langle \Psi ,t|{\hat {A}}|\Psi ,t\rangle =\langle \Psi ,0|e^{i{\hat {H}}t/\hbar }{\hat {A}}\,e^{-i{\hat {H}}t/\hbar }|\Psi ,0\rangle

vil dermed også variere med tiden. Formen til dette uttrykket kan også beskrives som om tilstanden til systemet ikke forandrer seg, men at det er operatoren som blir tidsavhengige. Man sier da at man har en fremstilling i «Heisenberg-bildet» hvor tilstandsvektoren er konstant $|\Psi \rangle _{H}=|\Psi ,0\rangle ,$ og operatorene varierer med tiden som

{\hat {A}}_{H}(t)=e^{i{\hat {H}}t/\hbar }{\hat {A}}\,e^{-i{\hat {H}}t/\hbar }

Den samme forventningsverdien kan derfor skrives alternativt som $\langle {\hat {A}}\rangle (t)=\;_{H}\langle \Psi |{\hat {A}}_{H}(t)|\Psi \rangle _{H}.$

Ved derivasjon finnes den differensielle formen

{\begin{aligned}i\hbar {d \over dt}{\hat {A}}_{H}(t)&=-e^{i{\hat {H}}t/\hbar }{\hat {H}}{\hat {A}}e^{-i{\hat {H}}t/\hbar }+e^{i{\hat {H}}t/\hbar }{\hat {A}}{\hat {H}}e^{-i{\hat {H}}t/\hbar }\\&=[{\hat {A}}_{H}(t),{\hat {H}}]\end{aligned}}

for tidsutvikling av en operator i Heisenberg-bildet. Det er den samme loven som Heisenberg kom frem til i sitt arbeid som grunnla matrisemekanikken.^[18]

Stasjonære tilstander og energibasis

En stasjonær tilstand med energi E er definert å ha den enkle tidsavhengigheten

|E,t\rangle =|E\rangle e^{-iEt/\hbar }

hvor tilstanden $|E\rangle$ må være en egentilstand av Hamilton-operatoren ${\hat {H}}.$ For et vilkårlig sett av N ortonormerte basisvektorer kan den da skrives som

|E\rangle =\sum _{n=1}^{N}u_{n}|n\rangle

hvor $u_{n}=\langle n|E\rangle$ nå er sannsynlighhetsamplituden for å finne systemet $|E\rangle$ I tilstand $|n\rangle .$ Egenverdiligningen ${\hat {H}}|E\rangle =E|E\rangle$ i denne basisen tar dermed formen

\sum _{n=1}^{N}H_{mn}u_{n}=Eu_{m}

hvor tallene $H_{mn}=\langle m|{\hat {H}}|n\rangle$ er matriseelementene av Hamilton-operatoren. Disse ligningene for de ukjente sannsynlighhetsamplitudene utgjør nå et lineært ligningssett som kun har løsninger for bestemte verdier av E. De er dermed egenverdier E_n til Hamilton-operatoren og kan finnes ved å diagonalisere den tilsvarende N × N dimensjonell matrisen.^[16]

Tidsutviklingen til en vilkårlig tilstand $|\Psi \rangle$ følger fra den tidsavhengige Schrödinger-ligningen. Sannsynligheten for at denne tilstanden skal befinne seg i basistilstanden $|m\rangle$ ved tiden t er gitt ved amplituden $\psi _{m}(t)=\langle m|\Psi ,t\rangle .$ Dennes forandring med tiden følger derfor fra

i\hbar {\partial  \over \partial t}\langle m|\Psi ,t\rangle =\langle m|{\hat {H}}|\Psi ,t\rangle

Ved her å sette inn enhetsoperatoren ${\hat {I}}=\sum _{n}|n\rangle \langle n|,$ tar denne ligningen formen

i\hbar {d\psi _{m} \over dt}=\sum _{n=1}^{N}H_{mn}\psi _{n}(t)

som utgjør et sett av N lineære differensialligninger av første orden.^[16] De kan nå formelt løses ved å første uttrykke tilstanden $|\Psi \rangle$ i energibasisen $|E_{n}\rangle$ som egenvektorene til Hamilton-operatoren danner. Det gir

|\Psi \rangle =\sum _{n=1}^{N}C_{n}|E_{n}\rangle

hvor koeffisientene C_n spesifiserer tilstanden. Den har nå en tidsutvikling

|\Psi ,t\rangle =e^{-i{\hat {H}}t/\hbar }|\Psi \rangle =\sum _{n=1}^{N}C_{n}e^{-iE_{n}t/\hbar }|E_{n}\rangle

Dermed kan den generelle løsningen av den tidsavhengige Schrödinger-ligningen skrives som

\psi _{m}(t)=\langle m|\Psi ,t\rangle =\sum _{n=1}^{N}C_{n}e^{-iE_{n}t/\hbar }\langle m|E_{n}\rangle

og inneholder eksplisitt egenverdiene til Hamilton-operatoren. I tillegg avhenger den av sannsynlighetsamplitudene $\langle m|E_{n}\rangle$ som er m-komponentene til de tilsvarende egenvektorene.

I Heisenbergs første arbeid om matrisemekanikk benyttet han en slik energibasis hvor Hamilton-operatoren var representert ved en diagonal matrise.^[9]

Eksempel: Hydrogenmolekyl

Et system med bare to tilstander vil gi en enkel illustrasjon av denne kvantemekaniske formalismen. Hamilton-operatoren er da representert ved en 2×2 matrise og systemets tidsutvikling kan lett beregnes. For å være mer konkret, kan man tenke seg et ionisert hydrogenmolekyl. Det har ett elektron som er påvirket av to proton som man kan tenke seg ligger i ro. I den enkleste beskrivelsen av dette systemet tenker man seg at elektronet kan befinne seg ved det ene eller det andre protonet. Det tilsvarer å innføre N = 2 basistilstander $|1\rangle$ og $|2\rangle .$ En mer detaljert fremstilling av molekylet ville krevd en enda større basis, men dette minimale valget vil likevel gi nyttig informasjon om dets kvantefysikk.^[19]

Den tidsavhengige Schrödinger-ligningen gir nå de to ordnære differensialligningene

{\begin{aligned}i\hbar {d\psi _{1} \over dt}&=H_{11}\psi _{1}+H_{12}\psi _{2}\\i\hbar {d\psi _{2} \over dt}&=H_{21}\psi _{1}+H_{22}\psi _{2}\end{aligned}}

Da Hamilton-operatoren er hermitisk, må de to elementene H₁₁ = E₁ og H₂₂ = E₂ være reelle. I tillegg må man ut fra symmetrien til systemet ha at de er like store, E₁ = E₂ = E₀. De ikke-diagonale elementene H₁₂ og H₂₁ er av samme grunn komplekst konjugerte av hverandre, men kan velges reelle med den hensiktsmessige verdien -A ved et passende valg av basisvektorer. Hamilton-operatoren for dette systemet blir på denne måten representert ved matrisen

H={\begin{pmatrix}E_{0}&-A\\-A&E_{0}\end{pmatrix}}

hvor både E₀ og A antas å være positive størrelser. De ikke-diagonale elementene betyr at hvis elektronet befinner seg ved ett proton, har det en viss sannsynlighet for å hoppe over til det andre.^[19]

Elektronet kan være nær det ene eller det andre protonet i hydrogenmolekylet. Det tilsvarer de to kvantetilstandene $|1\rangle$ og $|2\rangle .$

Egenverdiene til systemet kan nå finnes direkte ved å legge sammen eller ved å trekke de to ligningene fra hverandre. Det gir at ψ₁ + ψ₂ er amplituden for en egentilstand med energi E₀ - A. Den tilsvarende egenvektorer er $|E_{+}\rangle =|1\rangle +|2\rangle .$ Likedan representerer ψ₁ - ψ₂ en egenvektor $|E_{-}\rangle =|1\rangle -|2\rangle$ med egenverdi E₀ + A. De utgjør de to stasjonære tilstandene for systemet. Hvis elektronet starter ut i en av disse tilstandene, vil sannsynligheten for at det forblir i samme tilstand, ikke forandre seg med tiden.

Hvis derimot elektronet i utgangspunktet ikke befinner seg i en energetisk egentilstand, vil sannsynligheten for å bli værende i denne, variere ettersom tiden går. Det kan man for eksempel se ved å anta at elektronet ved tiden t = 0 befinner seg i posisjon $|1\rangle .$ Løsning av de to ligningene gir da

\psi _{1}(t)=e^{-iE_{0}t/\hbar }\cos At/\hbar ,\;\;\;\;\psi _{2}(t)=ie^{-iE_{0}t/\hbar }\sin At/\hbar

Sannsynligheten for å være ved det ene eller ved det andre protonet vil da variere som $P_{1}=|\psi _{1}(t)|^{2}=\cos ^{2}\!At/\hbar$ og $P_{2}=|\psi _{2}(t)|^{2}=\sin ^{2}\!At/\hbar .$ Elektronet vil oscillere mellom de to protonene med en frekvens som er gitt ved det ikke-diagonale elementet A. Systemet er unitært i den forstand at $P_{1}+P_{2}=1$ og uttrykker bevarelse av sannsynlighet.

Den stasjonære tilstanden $|E_{+}\rangle$ representerer en bunden tilstand da den har lavere energi enn om elektronet sitter bundet til bare én av protonene. Tilstanden er symmetrisk i de to protonene og man kan ikke med sikkerhet si om elektronet er på det ene eller andre av disse. Det befinner seg på et vis mellom dem og holder molekylet sammen. I denne tilstanden er det plass til enda et elektron som gir et sterkere bundet, nøytralt hydrogenmolekyl. På grunn av Paulis eksklusjonsprinsipp vil et tredje elektron måtte plasseres i den energetisk høyere tilstanden $|E_{-}\rangle$ . Et negativt ladet hydrogenmolekyl vil dermed være ustabilt i overensstemmelse med hva som er kjent fra dets kjemi.^[20]

Posisjonsbasis

Hvis man betrakter en partikkel som kan klassisk kan befinne seg på et av en mengde diskrete punkter x₁, x₂, .., x_N i et større molekyl eller i en krystall, kan en man i en kvantemekanisk beskrivelse benytte et tilsvarende sett med basisvektorer $|x_{1}\rangle ,|x_{2}\rangle ,\ldots |x_{N}\rangle$ . De er ortonormerte på den måten at $\langle x_{i}|x_{j}\rangle =\delta _{ij}$ når man på høyre side benytter et Kronecker-delta. Identitetsoperatoren i denne basisen er dermed

{\hat {I}}=\sum _{n=1}^{N}|x_{n}\rangle \langle x_{n}|

En vilkårlig tilstandsvektor $|\psi \rangle$ kan da representeres ved N sannsynlighetsamplituder $\psi _{n}=\langle x_{n}|\psi \rangle$ som generelt vil variere med tiden.

Av større betydning er å betrakte en partikkel som kan bevege seg på en rett linje med en koordinat. Kalles denne for x, vil man da innføre kvantemekaniske basistilstander $|x\rangle .$ De må da betraktes som egenvektorer til en posisjonsoperator ${\hat {x}}$ slik at ${\hat {x}}|x\rangle =x|x\rangle .$

Da koordinaten x varierer kontinuerlig , vil det tilsvarende Hilbert-rommet dermed få uendelig mange dimensjoner. Som for det diskrete tilfellet er det nå naturlig å definere identitetsoperatoren ved integralet

{\hat {I}}=\int _{-\infty }^{\infty }\!dx\,|x\rangle \langle x|

som har et abstrakt innhold, men kan benyttes på en konkret måte. For eksempel, en tilstand $|x'\rangle .$ kan skrives som

|x'\rangle ={\hat {I}}|x'\rangle =\int _{-\infty }^{\infty }\!dx\,|x\rangle \langle x|x'\rangle

For at dette sal være konsistent, må man derfor ha den kontinuerlige normeringen

\langle x|x'\rangle =\delta (x-x')

som uttrykkes ved Diracs deltafunksjon. For en vilkårlig funksjon f(x ) er den definert ved integralet

\int _{-\infty }^{\infty }\!dx\,f(x)\delta (x-a)=f(a)

Den bidrar bare i punktet x = a og er null ellers. Denne singulære egenskapen er ikke noe problem i praktiske anvendelser av funksjonen. På samme måte vil representasjon av operatorer i denne basisen gi opphav til matriser med kontinuerlige indekser. Likevel vil den formelle strukturen av Diracs kvantemekanikk ble bevart uten særlige forandringer.^[17]

Når partikkelen befinner seg i en generell tilstand $|\psi \rangle$ , er sannsynlighetsamplituden for at den befinner seg i posisjon x gitt ved projeksjonen

\psi (x)=\langle x|\psi \rangle

Dette er bølgefunksjonen til partikkelen og kan betraktes som komponenten av tilstandsvektoren i x-retning.

Translasjoner og impuls

For partikler som kan bevege seg på en åpen linje, kan vi fritt velge origo hvor vi vil. Det tilsvarer at i stedet for basisvektorene $|x\rangle$ kan vi benytte et nytt sett

|x'\rangle =|x+a\rangle ={\hat {T}}(a)|x\rangle

som finnes ved bruk av «translasjonsoperatoren» ${\hat {T}}(a).$ På samme måte som tidsutviklingsoperatoren ${\hat {U}}(t)$ foretar en forflytning av systemet i tid, vil translasjonsoperatoren forflytte systemet i rommet. Den må på samme måte være en unitær operator som kan skrives på den generelle formen

{\hat {T}}(a)=e^{-i{\hat {p}}a/\hbar }

hvor ${\hat {p}}$ er en hermitisk operator. Den er generator for infinitesimale eller veldig korte translasjoner i rommet.^[18]

Under en endelig translasjon vil bølgefunksjonen forandres til

\psi (x+a)=\langle x+a|\psi \rangle =\langle x|e^{i{\hat {p}}a/\hbar }|\psi \rangle

I grensen der a → 0, er derfor forandringen generelt gitt ved

{\begin{aligned}&\psi (x)+a{\partial \psi  \over \partial x}=\langle x|{\hat {I}}+{i \over \hbar }{\hat {p}}a|\psi \rangle \\&=\psi (x)+{i \over \hbar }a\langle x|{\hat {p}}|\psi \rangle \end{aligned}}

På denne måten kommer man frem til det viktige resultatet

\langle x|{\hat {p}}|\psi \rangle =-i\hbar {\partial  \over \partial x}\langle x|\psi \rangle

for denne generatoren. Da den er en hermitisk operator, vil den ha reelle egenverdier. Skriver man de tilsvarende egenvektorene som $|p\rangle$ med ${\hat {p}}|p\rangle =p|p\rangle ,$ vil bølgefunksjonen $\psi _{p}(x)=\langle x|p\rangle$ for denne egentilstanden oppfylle den enkle differensialligningen

p\,\psi _{p}(x)=-i\hbar {\partial  \over \partial x}\psi _{p}(x)

Løsningen kan skrives som den plane bølgen

\psi _{p}(x)=\langle x|p\rangle =e^{ipx/\hbar }

når man setter dens amplitude til å være lik med én. Dette er bølgefunksjonen for en fri partikkel med impuls p. Generatoren ${\hat {p}}$ for translasjoner langs x-aksen er derfor impulsoperatoren for samme retning.^[18]

Ut fra dette ser man at Schrödingers bølgemekanikk oppstår som fremstilling av en mer generell kvantemekanikk hvor man har valgt å benytte en koordinatbasis. Generelt har man nå at

\langle x|{\hat {p}}^{n}|\psi \rangle =(-i\hbar \partial _{x})^{n}\langle x|\psi \rangle

og derfor

\langle x|F({\hat {x}},{\hat {p}})|\psi \rangle =F(x,-i\hbar \partial _{x})\langle x|\psi \rangle

Hvis ${\hat {F}}=F({\hat {x}},{\hat {p}})$ er en hermitisk operator, er rekkefølgen til operatorene ${\hat {x}}$ og ${\hat {p}}$ viktig der de opptrer sammen. Dette kan tydeliggjøres ved å regne ut amplituden

\langle x|{\hat {x}}{\hat {p}}|\psi \rangle =x\langle x|{\hat {p}}|\psi \rangle =-ix\hbar \partial _{x}\psi

Sammenlignes den med den tilsvarende amplituden

\langle x|{\hat {p}}{\hat {x}}|\psi \rangle =-i\hbar \partial _{x}(x\psi )=-i\hbar (\psi +x\partial _{x}\psi ),

finnes nå ved subtraksjon at kommutatoren

[{\hat {x}},{\hat {p}}]=i\hbar

da det funne resultat må være gyldig for alle funksjoner $\psi (x).$ Det var Heisenberg som kom frem til denne sammenhengen i sitt første arbeid om matrisemekanikk, men det var Max Born som innså dens kanoniske betydning. Den er risset inn på hans gravstein i Göttingen.

Impulsbasis

Egenvektorene $|p\rangle$ til impulsoperatoren ${\hat {p}}$ danner et fullstendig sett og kan benyttes som en ny basis i Hilbert-rommet. Den er nå normert på en tilsvarende måte som for posisjonsbasisen. Det følger fra innsettelse av en enhetsoperator som gir

{\begin{aligned}\langle p'|p\rangle &=\langle p'|{\hat {I}}|p\rangle =\int _{-\infty }^{\infty }\!dx\,\langle p'|x\rangle \langle x|p\rangle =\int _{-\infty }^{\infty }\!dx\,e^{i(p-p')x/\hbar }\\&=2\pi \hbar \,\delta (p'-p)\end{aligned}}

når man benytter standardintegralet som definerer delta-funksjonen.

På lignende måte kan innføre en bølgefunksjon i dette impulsrommet som representasjon av en tilstand $|\psi \rangle .$ Den kan defineres ved komponenten ${\bar {\psi }}(p)=\langle p|\psi \rangle$ og er en projeksjonen av tilstandsvektoren på basisvektoren. Sammenhengen med den tilsvarende bølgefunksjonen i koordinatrommet følger nå på samme vis fra

{\bar {\psi }}(p)=\int _{-\infty }^{\infty }\!dx\,\langle p|x\rangle \langle x|\psi \rangle =\int _{-\infty }^{\infty }\!dx\,\psi (x)\,e^{-ipx/\hbar }

som viser at de er hverandres Fourier-transformerte. Den inverse transformasjonen er derfor

\psi (x)=\int _{-\infty }^{\infty }\!{dp \over 2\pi \hbar }{\bar {\psi }}(p)\,e^{ipx/\hbar }

som igjen følger fra definisjonen av delta-funksjonen.

Mens impulsoperatoren kan her behandles som et vanlig tall, vil posisjonsoperatoren ${\hat {x}}$ virke som en derivasjon. Det følger fra

\langle p|{\hat {x}}|x\rangle =x\langle p|x\rangle =xe^{-ipx/\hbar }=i\hbar \partial _{p}\langle p|x\rangle

som gir mer generelt for en vilkårlig tilstand at

\langle p|{\hat {x}}|\psi \rangle =i\hbar \partial _{p}\langle p|\psi \rangle

Posisjonsoperatoren kan derfor erstattes med derivasjonsoperatoren $i\hbar \partial _{p}$ når den virker på bølgefunksjoner i impulsrommet.

Tre dimensjoner

For å lokalisere en partikkel som kan bevege seg i et tredimensjonalt rom, kan man bruke kartesiske koordinater. Dens posisjon er da gitt ved vektoroperatoren

{\hat {\mathbf {x} }}=\sum _{a=1}^{3}{\hat {x}}_{a}\mathbf {e} _{a}.

med ortonormerte basisvektorer $\mathbf {e} _{a}\cdot \mathbf {e} _{b}=\delta _{ab}.$ Den har egentilstander $|\mathbf {x} \rangle =|x\rangle |y\rangle |z\rangle$ slik at ${\hat {\mathbf {x} }}|\mathbf {x} \rangle =\mathbf {x} |\mathbf {x} \rangle .$ Normeringen tas over fra én dimensjon og er derfor

\langle \mathbf {x} |\mathbf {x} '\rangle =\delta (\mathbf {x} -\mathbf {x} ')

når man skriver $\delta (\mathbf {x} -\mathbf {x} ')=\delta (x-x')\delta (y-y')\delta (z-z').$ Enhetsoperatoren I tre dimensjoner er derfor

{\hat {I}}=\int \!d^{3}x\,|\mathbf {x} \rangle \langle \mathbf {x} |

når man benytter denne normeringen.^[18]

Operatoren for translasjonen $\mathbf {x} \rightarrow \mathbf {x} '=\mathbf {x} +\mathbf {a} \;$ er

{\hat {T}}(\mathbf {a} )=e^{-i{\hat {\mathbf {p} }}\cdot \mathbf {a} /\hbar }

hvor ${\hat {\mathbf {p} }}$ er impulsoperatoren I tre dimensjoner. Dens egentilstander $|\mathbf {p} \rangle$ får nå normeringen

\langle \mathbf {p} '|\mathbf {p} \rangle =(2\pi \hbar )^{3}\delta (\mathbf {p} '-\mathbf {p} )

og kan representeres ved bølgefunksjonen

\psi _{\mathbf {p} }(\mathbf {x} )=\langle \mathbf {x} |\mathbf {p} \rangle =e^{i\mathbf {p} \cdot \mathbf {x} /\hbar }

i koordinatrommet. På tilsvarende vis er en generell tilstand $|\psi \rangle$ representert ved bølgefunksjon

\psi (\mathbf {x} )=\langle \mathbf {x} |\psi \rangle

Den er relatert til en ekvivalent bølgefunksjon ${\bar {\psi }}(\mathbf {p} )=\langle \mathbf {p} |\psi \rangle$ i impulsrommet ved Fourier-integralet

\psi (\mathbf {x} )=\int \!{d^{3}p \over (2\pi \hbar )^{3}}{\bar {\psi }}(\mathbf {p} )\,e^{i\mathbf {p} \cdot \mathbf {x} /\hbar }

Impulsoperatoren ${\hat {\mathbf {p} }}$ er representert ved $-i\hbar \partial _{\mathbf {x} }$ i koordinatrommet hvor $\partial _{\mathbf {x} }$ er nabla-operatoren ${\boldsymbol {\nabla }}$ med komponenter $(\partial _{x},\partial _{y},\partial _{z}).$ Egenverdiligningen ${\hat {H}}|\psi \rangle =E|\psi \rangle$ med Hamilton-operatoren

{\hat {H}}={{\hat {\mathbf {p} }}^{2} \over 2m}+V({\hat {\mathbf {x} }})

gir dermed den tidsuavhengige Schrödinger-ligningen

{\Big [}-{\hbar ^{2} \over 2m}{\boldsymbol {\nabla }}^{2}+V(\mathbf {x} ){\Big ]}\psi (\mathbf {x} )=E\psi (\mathbf {x} )

når den blir representert i det tredimensjonale koordinatrommet.

På tilsvarende vis er posisjonsoperatoren ${\hat {\mathbf {x} }}$ representert ved $i\hbar \partial _{\mathbf {p} }$ i impulsrommet som også kan benyttes til å gi en ny representasjon av Schrödinger-ligningen. Derimot vil den kanoniske kommutator i tre dimensjoner alltid være

[{\hat {x}}_{a},{\hat {p}}_{b}]=i\hbar \,\delta _{ab}

uansett hvordan disse to konjugerte operatorene blir representert.

Rotasjoner og dreieimpuls

Under rotasjon med en vinkel φ om z-aksen vil de to andre koordinatene forandres til

{\begin{aligned}x\rightarrow x'&=x\cos \phi -y\sin \phi \\y\rightarrow y'&=x\sin \phi +y\cos \phi \end{aligned}}

Når dreievinkelen blir tilstrekkelig liten δφ, kan man sette cosφ = 1 og sinφ = δφ. Koordinatforandringene blir dermed δx = x' - x = -yδφ og δy = y' - y = xδφ. Ved å benytte enhetsvektoren e_z langs z-aksen, kan denne forandringen skrives mer kompakt som δ r = δφ e_z × r. Generelt kan derfor effekten av den samme rotasjonen om en vilkårlig enhetsvektor n skrives

\delta \mathbf {r} =\mathbf {r} '-\mathbf {r} =\delta \phi \,\mathbf {n} \times \mathbf {r}

Det er derfor naturlig å betrakte δφ n = δ φ som en vektoriell vinkel som også angir retningen til rotasjonsaksen.

På samme måte som en klassisk translasjon av en posisjonsvektor fører til en tilsvarende translasjonsoperator, vil en rotasjon kvantemekanisk være gitt ved en rotasjonsoperator ${\hat {R}}$ definert ved

|\mathbf {r} \rangle \rightarrow |\mathbf {r} '\rangle ={\hat {R}}({\boldsymbol {\phi }})|\mathbf {r} \rangle

for en endelig rotasjon ${\boldsymbol {\phi }}=\phi \,\mathbf {n} .$ Operatoren må være unitær og vil derfor ha formen

{\hat {R}}({\boldsymbol {\phi }})=\exp(-{i \over \hbar }{\hat {\mathbf {L} }}\cdot {\boldsymbol {\phi }})

hvor $\;{\hat {\mathbf {L} }}\;$ er en hermitisk operator som genererer infinitesemale rotasjoner. Da vil bølgefunksjon $\psi (\mathbf {r} )=\langle \mathbf {r} |\psi \rangle$ gå over til å bli

\psi (\mathbf {r} +\delta \mathbf {r} )=\langle \mathbf {r} '|\psi \rangle =\psi (\mathbf {r} )+{i \over \hbar }\langle \mathbf {r} |{\hat {\mathbf {L} }}\cdot \delta {\boldsymbol {\phi }}|\psi \rangle

Da denne lille forandringen er

{\begin{aligned}\delta \psi (\mathbf {r} )&=\psi (\mathbf {r} ')-\psi (\mathbf {r} )=\delta \mathbf {r} \cdot {\boldsymbol {\nabla }}\psi \\&=(\delta {\boldsymbol {\phi }}\times \mathbf {r} )\cdot {\boldsymbol {\nabla }}\psi =\delta {\boldsymbol {\phi }}\cdot (\mathbf {r} \times {\boldsymbol {\nabla }})\psi ,\end{aligned}}

kommer man frem til det viktige resultatet

\langle \mathbf {r} |{\hat {\mathbf {L} }}|\psi \rangle =-i\hbar \,\mathbf {r} \times {\boldsymbol {\nabla }}\psi (\mathbf {r} )

Selv om det er her utledet i koordinatbasis, er likevel dreieimpulsoperatoren ${\hat {\mathbf {L} }}={\hat {\mathbf {r} }}\times {\hat {\mathbf {p} }}$ alltid generatoren for rotasjoner.^[14]

Aktive transformasjoner

Når rotasjonsoperatoren ${\hat {R}}({\boldsymbol {\phi }})$ utledes som her ved å ta den virke på basisvektorene, sies transformasjonen å være passiv. I dette bildet påvirkes ikke tilstandsvektoren $|\psi \rangle$ av operasjonen. Men vektoren vil ha nye komponenter i den transformerte basisen

\psi (\mathbf {r} ')=\langle \mathbf {r} '|\psi \rangle =\langle \mathbf {r} |{\hat {R}}(-{\boldsymbol {\phi }})|\psi \rangle

da ${\hat {R}}^{\dagger }({\boldsymbol {\phi }})={\hat {R}}^{-1}({\boldsymbol {\phi }})={\hat {R}}(-{\boldsymbol {\phi }}).$ Denne sammenhengen kan alternativt forstås som at den samme transformasjonen virker på selve tilstandsvektoren og dreier den i motsatt retning $-{\boldsymbol {\phi }}.$ En aktiv rotasjon med rotasjonsvinkel ${\boldsymbol {\phi }}$ vil da være

|\psi \rangle \rightarrow |\psi '\rangle ={\hat {R}}({\boldsymbol {\phi }})|\psi \rangle

Den påvirker ikke basisvektorene slik at komponentene til den roterte tilstandsvektoren blir

\psi '(\mathbf {r} )=\langle \mathbf {r} |\psi '\rangle =\langle \mathbf {r} |{\hat {R}}({\boldsymbol {\phi }})|\psi \rangle

uttrykt i de opprinnelige koordinatene. Denne nye funksjonen har den spesielle egenskapen at $\;\psi '(\mathbf {r'} )=\psi (\mathbf {r} ).$ Det er en konsekvens av det unitære kravet ${\hat {R}}^{\dagger }{\hat {R}}={\hat {I}}$ og gjelder også for translasjoner i rommet. For de fleste anvendelser av kvantemekanikken benyttes slike aktive transformasjoner.

Videre utvikling

Men de grunnleggende idéene til kvantemekanikken kom fra beskrivelsen av enkelte partikler, skyldtes dens videre utvikling en utvidet forståelse av egenskapene til mange identiske partikler. Allerede i 1924 hadde den indiske fysiker Satyendra Nath Bose vist hvordan Plancks teori for varmestrålingen kunne forklares ved å benytte en ny opptelling av kvantetilstandene for et slikt system. Einstein forsto med en gang at denne nye kvantestatistikken også kan benyttes for massive partikler og kalles nå for Bose-Einstein-statistikk. Den er tett knyttet til bølgemekanikken og var det problemet Schrödinger arbeidet med da han utviklet sin bølgeligning. Partikler som beskrives ved denne type statistisk mekanikk kalles nå for bosoner.^[1]

Spinn-1/2 og fermioner

For å forklare oppbyggingen av det periodiske systemet og egenskapene til karakteristisk røntgenstråling innførte Wolfgang Pauli i 1925 sitt eksklusjonsprinsipp for elektroner. Det sa at kun ett elektroner kan befinne seg i samme kvantetilstand når man tar hensyn til dets spinn-1/2 som ble oppdaget senere samme år.

Basert på dette prinsippet beregnet Enrico Fermi i 1926 de statistiske egenskapene til et stort antall elektroner bundet i et tredimensjonalt, harmonisk oscillator potensial. Lignende betraktninger av Paul Dirac som benyttet at bølgefunksjonen for et slikt system må være antisymmetrisk, førte til Fermi-Dirac-statistikk. Den gjelder for partikler med halvtallig spinn eller fermioner, mens Bose-Einstein statistikk må anvendes for partikler med heltallig spinn.^[14]

Andrekvantisering

En helt ny måte å beskrive kvantesystemer med mange partikler ble klarlagt av Dirac i 1927 da han viste hvordan det elektromagnetiske feltet kan kvantiseres. På denne måten ble bølge–partikkel-dualiteten mellom et foton som på den ene siden kan omtales som en partikkel og samtidig beskrives som en bølge, bedre forstått. Denne første feltkvantisering blir i dag vanligvis omtalt som kvantisert strålingsteori som etter hvert utviklet seg til dagens kvanteelektrodynamikk.

Da det ikke lenger var posisjonen og impulsen til en partikkel som kvantiseres, men det klassiske Maxwell-feltet styrt av Maxwells ligninger, ble denne utvidelsen omtalt som en andrekvantisert teori. Da er ikke lenger antall partikler konstant, men de kan oppstå og forsvinne i forskjellige prosesser. Når et foton for eksempel blir sendt ut fra et atom ved en overgang fra et energinivå til et lavere nivå, så blir fotonet skapt i det øyeblikket. Det eksisterte ikke i atomet på et tidligere tidspunkt. Teorien vil derfor inneholde kreasjon og annihilasjonsoperator som adderer eller fjerner partikler fra systemet.^[1]

Omtrent på samme tid utviklet Pascual Jordan og Oskar Klein en tilsvarende beskrivelse for ikke-relativistiske partikler. Deres bølgeligning vil da være den tidsavhengige Schrödinger-ligningen hvor bølgefunksjonen må betraktes som en felt-funksjon for disse identiske bosonene.

Sammen med Eugene Wigner viste Jordan noen måneder senere hvordan også ikke-relativistiske fermioner kan beskrives på denne måten. Ved utsendelse av lys fra et atom, er det da ikke bare et foton som blir skapt, men et elektron blir fjernet fra en tilstand i atomet og et nytt elektron blir skapt i en ny tilstand med lavere energi.

Relativistisk kvantemekanikk

Da Schrödinger utviklet sin kvantemekaniske bølgeligning, ville han at den skulle være i overensstemmelse med Einsteins spesielle relativitetsteori. Ved å anvende den på hydrogenatomet kom han frem til Bohrs formel for energinivåene, men også med mindre, relativistiske korreksjoner til disse. De viste seg å ikke stemme med målte verdier. Han forkastet derfor denne relativistiske bølgeligningen som senere har fått navnet Klein-Gordon-ligningen og publiserte bare den ikke-relativistiske Schrödinger-ligningen.^[8]

Et annet og viktigere problem med den relativistiske bølgeligningen var at den ikke kunne gi en positiv sannsynlighetstetthet. Grunnen var at den i tillegg til de andrederiverte med hensyn på de romlige koordinatene, også inneholdt en andrederivert med hensyn på tiden. Denne observasjon fikk Dirac til å søke etter en relativistisk bølgeligning som var lineær i de førstederiverte med hensyn på alle fire koordinater. Resultatet ble hans relativistiske Dirac-ligning som ble publisert i 1928. Den viste seg også å gi relativistiske korreksjoner til energinivåene i hydrogenatomet som var i overensstemmelse med observasjonene.^[21]

I tillegg ble det klart at ligningen til Dirac automatisk beskriver partikler med spinn s = 1/2 som man allerede visste elektronet måtte ha. Dette spinnet koblet også til et ytre magnetfelt med en gyromagnetisk faktor g = 2. Denne verdien er dobbelt så stor som den klassiske og var tidligere et mysterium.

Men både Klein-Gordon-ligningen og Dirac-ligningen ga opphav til nye problem. Det første ble påvist av Oskar Klein i 1929 da han beregnet spredning av elektroner mot en tilstrekkelig høy potensialbarriere. Han kom da frem til at det ble reflektert flere partikler enn det ble sendt inn, noe som synes å stride mot bevarelse av sannsynlighet i kvantemekanikken. Dette problemet er i ettertid blitt kalt for Kleins paradoks.^[21]

Det andre problemet var at begge disse relativistiske bølgeligningene forutsa frie partikler som kunne ha negative energier. Slike løsninger kan ikke aksepteres i klassisk fysikk. Dirac argumenterte med at alle disse uønskete tilstandene var fylt opp i en negativ bakgrunn eller «sjø» i overensstemmelse med Paulis eksklusjonsprinsipp for elektroner. En eksitasjon av et slikt elektron med negativ energi til en tilstand med positiv energi, ville skape et «hull i sjøen» som kunne observeres som en partikkel med positiv ladning. Han trodde først at det kunne være et proton, men Robert Oppenheimer påpekte i 1930 at da ville hydrogenatomet bli ustabilt ved at elektron og proton kunne annihihilere hverandre. Året etter konkluderte Dirac med at løsningene med negativ energi må beskrive elektronets antipartikkel som må ha samme masse og motsatt ladning. Vel ett år senere ble positronet oppdaget i kosmisk stråling.^[1]

Kvantefeltteori

Problemene rundt Kleins paradoks og partikler med negativ energi skyldes at både Klein-Gordon-ligningen og Dirac-ligningen var blitt benyttet som om de skulle gi en relativistisk beskrivelse av kun én partikkel. Tilstedeværelse av antipartikler kan generelt ikke unngås. Ligningene er ikke bølgeligninger på like fot med den ikke-relativistiske Schrödinger-ligningen, men dermot bevegelsesligninger for relativistiske felt. Mens Klein-Gordon-ligningen beskriver et bosonfelt for partikler med spinn s = 0, gjelder Dirac-ligningen for fermionfelt med spinn s = 1/2.

Den første kvantisering av Maxwell-feltet for fotoner ble gjort av Dirac i 1927. Året etterpå viste Jordan og Pauli hvordan dette var konsistent med spesiell relativitetsteori. Den første, systematiske kvantisering av felt for massive partikler ble lansert av Heisenberg og Pauli i 1929. Dermed var en ikke-kovariant kvanteelektrodynamikk etablert hvor både partikler og det elektromagnetiske feltet var kvantiserte. Det var nå mulig å beregne spredningstverrsnittet for relativistisk Compton-spredning som kan uttrykkes ved Klein-Nishinas formel.^[22]

Relativistisk kvanteelektrodynamikk omhandlet de første årene bare fotoner og elektroner. I 1932 publiserte Enrico Fermi en mer pedagogisk fremstilling av teorien som fikk stor betydning.^[23] Samme år ble nøytronet påvist som en fri partikkel. Tidligere hadde man indirekte betraktet det i atomkjernen som en bunden tilstand av et proton og et elektron. Ved betahenfall ble elektronet sendt ut sammen med et nøytrino, og nøytronet gikk over til å bli et proton. Hvis nå elektronet likevel ikke fantes bundet i atomkjernen, ble spørsmålet hvor det kom fra i denne prosessen. Svaret kom med Fermis vekselvirkning som inneholder kvantefeltoperatorer for elektronet og nøytrinoet. Begge må da tenkes skapt fra intet. Denne forklaringen som stemte i detalj med nøyaktige observasjoner, kom Fermi med allerede i 1933 og styrket troen på at relativistisk kvantefeltteori ville gi en korrekt beskrivelse av egenskapene til også andre elementærpartikler.

I de følgende årene ble det konstatert at kvantefeltteoriene ga divergent resultat for de fleste prosesser når man foretok beregninger til høyere orden i perturbasjonsteori. Først etter andre verdenskrig ble disse nye problemene forstått og løst med en fremgangsmåte som nå omtales som renormalisering. Siden er det blitt utviklet kvantefeltteorier for alle elementærpartiklene. Det har gjort det mulig å beregne deres egenskaper og vekselvirkninger i full overennsstemmelse med alle observasjoner. Disse teoriene utgjør det som i dag omtales som Standardmodellen.^[22]

Feynmans veiintegral

Etter andre verdenskrig utviklet Richard Feynman en ny formulering av kvantemekanikken som på noen måter var mer generell enn den som tidligere var etablert av Heisenberg og Schrödinger. Den tok sitt utgangspunkt i den klassiske Lagrange-funksjonen istedenfor Hamilton-funksjonen som den kvantemekaniske Hamilton-operatoren bygger på. Denne gir energien til systemet og peker dermed ut en bestemt retning i det firedimensjonale Minkowski-rommet. Av den grunn kan dette gi vanskeligheter med å bevare overensstemmelse med Einsteins spesielle relativitetsteori. Derimot er Lagrange-funksjonen en skalar størrelse slik at disse problemene med relativistisk invarians ikke er tilstede i Feynmans formulering.

Basert på Lagrange-funksjonen for et system kan dets klassiske virkning beregnes. Feynman viste at denne kunne benyttes til å gi hver mulig tidsutvikling som et system kunne ha, en kvantemekanisk sannsynlighetsamplitude. Den totale amplituden for en overgang fra en tilstand til en annen, ville da være gitt ved summen av alle enkeltamplitudene for hver slik vei. I den kontinuerlige grensen går denne summen over i et veiintegral. Dette kan formuleres både for ikke-relativistiske partikler og relativistiske kvantefeltteorier.^[24]

De første årene ble Feynmans veiintegral lite brukt i konkrete beregninger. Men i det arbeidet som var forbundet med å etablere Standardmodellen for elementærpartiklene, viste det seg snart at denne alternative formuleringen hadde store fordeler. I dag er det denne som dominerer alle teoretisk betraktninger på dette feltet.^[25]

Se også

Referanser

^ ^a ^b ^c ^d ^e ^f ^g A. Pais, Inward Bound, Oxford University Press, England (1986). ISBN 0-19-851971-0.
^ ^a ^b ^c ^d ^e D. Bohm, Quantum Theory, Dover Books, New York (1989). ISBN 0-486-65969-0.
^ A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt, Annalen der Physik 322 (6), 132-148 (1905). PDF
^ R.P. Feynman, Photons - Corpuscles of Light, forelesning ved universitetet i Auckland (1979).
^ H. Kragh, Niels Bohr and the Quantum Atom, Oxford University Press, Oxford (2012). ISBN 0-19-965498-0.
^ A. Sommerfeld, Atombau und Spektrallinien, Verlag von Friedrich Vieweg & Sohn, Braunschweig (1919).
^ ^a ^b M. Born, Atomic Physics, Blackie & Son Limited, Glasgow (1962).
^ ^a ^b ^c ^d ^e M. Longair, Quantum Concepts in Physics, Cambridge University Press, England (2014). ISBN 978-1-107-01709-2.
^ ^a ^b M. Born, Problems of Atomic Dynamics, MIT Press, Massachusetts (1970). ISBN 0-262-52019-2. Forelesninger ved MIT 1925-26.
^ ^a ^b ^c S. Weinberg, Lectures on Quantum Mechanics, Cambridge University Press, England (2015). ISBN 978-1-107-11166-0.
^ W. Pauli, Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik, Zeitschrift für Physik 36 (5), 336–363 (1926). PDF
^ P.A.M. Dirac, Quantum mechanics and a preliminary investigation of the hydrogen atom, Proc. Roy. Soc. A110, 561-579 (1926).
^ ^a ^b ^c ^d ^e D.J. Griffiths, Quantum Mechanics, Pearson Education International, Essex (2005). ISBN 1-292-02408-9.
^ ^a ^b ^c ^d A.S. Davydov, Quantum Mechanics, Pergamon Press, London (1965).
^ P. Ball, Beyond Weird, Penguin Random House, London (2018). ISBN 978-1-84792457-5.
^ ^a ^b ^c ^d R.P. Feynman, Lectures on Physics, Volume III, Caltech (1964). Online versjon
^ ^a ^b ^c ^d P.A.M. Dirac, The Principles of Quantum Mechanics, Oxford at the Clarendon Press, Oxford (1947).
^ ^a ^b ^c ^d ^e E. Merzbacher, Quantum Mechanics, John Wiley & Sons, New York (1961).
^ ^a ^b R.P. Feynman, Other Two-State Systems, Feynman Lectures at Caltech (1964).
^ P.W. Atkins, Physical Chemistry, Oxford University Press, Oxford (1988). ISBN 0-19-855186-X.
^ ^a ^b J.D. Bjorken and S.D. Drell, Relativistic Quantum Mechanics, McGraw-Hill Book Company, New York (1964).
^ ^a ^b S.S. Schweber, QED and the Men Who Made It, Princeton University Press, New Jersey (1994). ISBN 0-691-03327-7.
^ E. Fermi, Quantum Theory of Radiation, Reviews of Modern Physics 4 (1), 87–132 (1932). PDF
^ R.P. Feynman and A.R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill Book Company, New York (1965).
^ M.E. Peskin and D.V. Schroeder, An Introduction to Quantum Field Theory, Addison-Wesley, Reading MA (1995). ISBN 0-201-50397-2.

Eksterne lenker

Kvantefysisk abrakadabra - artikkel fra forskning.no 5.10.05
Den knøttlille fysikken- artikkel fra forskning.no 20.4.13

[Pais-1-1] ^ ^a ^b ^c ^d ^e ^f ^g A. Pais, Inward Bound, Oxford University Press, England (1986). ISBN 0-19-851971-0.

[Bohm-2] D. Bohm, Quantum Theory, Dover Books, New York (1989). ISBN 0-486-65969-0.

[Einstein-1-3] A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt, Annalen der Physik 322 (6), 132-148 (1905). PDF

[Feynman-photon-4] R.P. Feynman, Photons - Corpuscles of Light, forelesning ved universitetet i Auckland (1979).

[Kragh-1-5] H. Kragh, Niels Bohr and the Quantum Atom, Oxford University Press, Oxford (2012). ISBN 0-19-965498-0.

[Sommerfeld-6] A. Sommerfeld, Atombau und Spektrallinien, Verlag von Friedrich Vieweg & Sohn, Braunschweig (1919).

[Born-7] M. Born, Atomic Physics, Blackie & Son Limited, Glasgow (1962).

[Longair-8] M. Longair, Quantum Concepts in Physics, Cambridge University Press, England (2014). ISBN 978-1-107-01709-2.

[MIT-9] M. Born, Problems of Atomic Dynamics, MIT Press, Massachusetts (1970). ISBN 0-262-52019-2. Forelesninger ved MIT 1925-26.

[Weinberg-10] S. Weinberg, Lectures on Quantum Mechanics, Cambridge University Press, England (2015). ISBN 978-1-107-11166-0.

[Pauli-11] W. Pauli, Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik, Zeitschrift für Physik 36 (5), 336–363 (1926). PDF

[12] P.A.M. Dirac, Quantum mechanics and a preliminary investigation of the hydrogen atom, Proc. Roy. Soc. A110, 561-579 (1926).

[Griffiths-13] D.J. Griffiths, Quantum Mechanics, Pearson Education International, Essex (2005). ISBN 1-292-02408-9.

[Davydov-14] A.S. Davydov, Quantum Mechanics, Pergamon Press, London (1965).

[Ball-15] P. Ball, Beyond Weird, Penguin Random House, London (2018). ISBN 978-1-84792457-5.

[RPF-QM-16] R.P. Feynman, Lectures on Physics, Volume III, Caltech (1964). Online versjon

[Dirac-QM-17] P.A.M. Dirac, The Principles of Quantum Mechanics, Oxford at the Clarendon Press, Oxford (1947).

[Merzbacher-18] E. Merzbacher, Quantum Mechanics, John Wiley & Sons, New York (1961).

[RPF-mol-19] R.P. Feynman, Other Two-State Systems, Feynman Lectures at Caltech (1964).

[Atkins-20] P.W. Atkins, Physical Chemistry, Oxford University Press, Oxford (1988). ISBN 0-19-855186-X.

[BD-21] J.D. Bjorken and S.D. Drell, Relativistic Quantum Mechanics, McGraw-Hill Book Company, New York (1964).

[Schweber-22] S.S. Schweber, QED and the Men Who Made It, Princeton University Press, New Jersey (1994). ISBN 0-691-03327-7.

[Fermi-1-23] E. Fermi, Quantum Theory of Radiation, Reviews of Modern Physics 4 (1), 87–132 (1932). PDF

[RPF-Hibbs-24] R.P. Feynman and A.R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill Book Company, New York (1965).

[PS-25] M.E. Peskin and D.V. Schroeder, An Introduction to Quantum Field Theory, Addison-Wesley, Reading MA (1995). ISBN 0-201-50397-2.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

Fagområder innen fysikk
Akustikk · Astrofysikk · Kondenserte fasers fysikk · Elektromagnetisme · Geofysikk · Mekanikk · Klassisk mekanikk · Kontinuumsmekanikk · Kvantemekanikk · Termodynamikk · Kjernefysikk · Optikk · Partikkelfysikk · Psykofysikk · Kvantefeltteori · Relativitetsteorien (spesiell · generell)
Kategori