Informatics Educational Institutions & Programs

有限状态机（英語：finite-state machine，縮寫：FSM）又稱有限状态自动机（英語：finite-state automaton，縮寫：FSA），简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型。

概念和术语

状态存储关于过去的信息，就是说：它反映从系统开始到现在时刻的输入变化。转移指示状态变更，并且用必须满足确使转移发生的条件来描述它。动作是在给定时刻要进行的活动的描述。有多种类型的动作：

进入动作（entry action）：在进入状态时进行
退出动作（exit action）：在退出状态时进行
输入动作：依赖于当前状态和输入条件进行
转移动作：在进行特定转移时进行

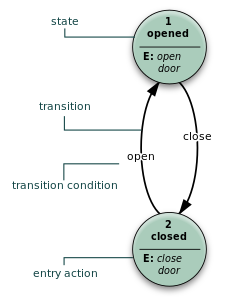
FSM（有限状态机）可以使用上面图1那样的状态图（或状态转移图）来表示。此外可以使用多种类型的状态转移表。下面展示最常见的表示：当前状态（B）和条件（Y）的组合指示出下一个状态（C）。完整的动作信息可以只使用脚注来增加。包括完整动作信息的FSM定义可以使用状态表。

**状态转移表**
当前状态→ 条件↓	状态A	状态B	状态C
条件X	…	…	…
条件Y	…	状态C	…
条件Z	…	…	…

除了建模这里介绍的反应系统之外，有限状态自动机在很多不同领域中是重要的，包括电子工程、语言学、计算机科学、哲学、生物学、数学和逻辑学。有限状态机是在自动机理论和计算理论中研究的一类自动机。在计算机科学中，有限状态机被广泛用于建模应用行为、硬件电路系统设计、软件工程，编译器、网络协议、和计算与语言的研究。

分类

有两个不同的群组：接受器／识别器和变换器。

接受器和识别器

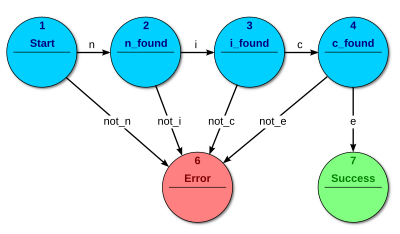
接受器和识别器（也叫做序列检测器）产生一个二元输出，说要么“是”要么“否”来回答输入是否被机器接受。所有FSM的状态被称为要么接受要么不接受。在所有输入都被处理了的时候，如果当前状态是接受状态，输入被接受，否则被拒绝。作为规则，输入是符号（字符）；动作不使用。图2中的例子展示了接受单词"nice"的有限状态自动机，在这个FSM中唯一的接受状态是状态7。

机器还可以被描述为定义了一个语言，它包含了这个机器所接受而非拒绝的所有字词；我们称这个语言被这个机器接受。通过定义，FSM接受的语言是正则语言 - 就是说，如果一个语言被某个FSM接受，那么它是正则的（cf. Kleene的定理）。

开始状态

开始状态通常用“没有起点的箭头”指向它来表示^[1]

图3：一個FSM的示意圖：检测二进制数是否含有偶数个0，其中 $S_{1}$ 是**接受狀態**

接受状态（或稱最終狀態）是一個机器回報到目前為止，輸入字串屬於它所接受的內容之狀態。狀態圖中通常將其標示为双圓圈。
開始狀態也可以是接受狀態，此情況下自動機會接受空字串。如果開始狀態不是接受狀態，且沒有可以連到任何接受狀態的箭頭，那麼此自動機就不會「接受」任何輸入。
一个接受状态的例子如图3：一台判断输入二进位字串是否含有偶数个0的确定有限自动机（DFA）。
S₁ 代表着已经输入了偶数个0，因此S₁ 即為接受状态（同時亦為開始狀態）。若輸入含有偶數個0（包含沒有0的字串），則此機器會以接受狀態來結束。
被這台DFA接受的字串，舉例來說是ε（空字串）, 1, 11, 11…, 00, 010, 1010, 10110…等等。

变换器

变换器使用动作基于给定输入和／或状态生成输出。它们用于控制应用。常分为两种类型：

Moore机

只使用进入动作的FSM，就是说输出只依赖于状态。Moore模型的好处是行为的简单性。图1的例子展示了一个电梯门的Moore FSM。这个状态机识别两个命令：“command_open”和“command_close”触發状态变更。在状态“Opening”中的进入动作 (E:)开启电机开门，在状态“Closing”中的进入动作以反方向开启电机关门。状态“Opened”和“Closed”不进行任何动作。它们信号通知外部世界（比如其他状态机）情况：“门开着”或“门关着”。

Mealy机

只使用输入动作的FSM，就是说输出依赖于输入和状态。Mealy FSM的使用经常导致状态数目的简约。在图4中的例子展示了实现同上面Moore机同样行为的Mealy FSM（行为依赖于实现的FSM执行模型，比如对虚拟FSM可工作但对事件驱动FSM不行）。有两个输入动作（I:）：“开启电机关门如果command_close下达”和“反向开启电机开门如果command_open下达”。

在实践中经常使用混合模型。

进一步可区分为确定型（DFA）和非确定型（NDFA、GNFA）自动机。在确定型自动机中，每个状态对每个可能输入只有精确的一个转移。在非确定型自动机中，给定状态对给定可能输入可以没有或有多于一个转移。这个区分在实践而非理论中更有用，因为存在算法把任何NDFA转换成等价的DFA，尽管这种转换一般会增加自动机的复杂性。

只有一个状态的FSM叫做组合FSM并只使用输入动作。这个概念在多个FSM要一起工作的情况下是有用的，这时把纯组合部分看作一种形式的FSM来适合设计工具可能是方便的。

FSM逻辑

FSM的下一个状态和输出是由输入和当前状态决定的。FSM逻辑在图5中展示。

数学模型

依据类型不同有多种定义。接受器有限状态机是五元组 $(\Sigma ,S,s_{0},\delta ,F)$ ，这里的：

$\Sigma$ 是输入字母表（符号的非空有限集合）。
$S$ 是状态的非空有限集合。
$s_{0}$ 是初始状态，它是 $S$ 的元素。在非确定有限状态自动机中， $s_{0}$ 是初始状态的集合。
$\delta$ 是状态转移函数： $\delta :S\times \Sigma \rightarrow S$ 。
$F$ 是最终状态的集合， $S$ 的（可能为空）子集。

变换器有限状态自动机是六元组 $(\Sigma ,\Gamma ,S,s_{0},\delta ,\omega )$ ，这里的：

$\Sigma$ 是输入字母表（符号的非空有限集合）。
$\Gamma$ 是输出字母表（符号的非空有限集合）。
$S$ 是状态的非空有限集合。
$s_{0}$ 是初始状态，它是 $S$ 的元素。在非确定有限状态自动机中， $s_{0}$ 是初始状态的集合。
$\delta$ 是状态转移函数： $\delta :S\times \Sigma \rightarrow S$ 。
$\omega$ 是输出函数。

如果输出函数是状态和输入字母表的函数（ $\omega :S\times \Sigma \rightarrow \Gamma$ ），则定义对应于Mealy模型，它可以建模为Mealy机。如果输出函数只依赖于状态 ( $\omega :S\rightarrow \Gamma$ ），则定义对应于Moore模型，它可建模为Moore机。根本没有输出函数的有限状态机叫做半自动机或转移系统。

优化

优化一个FSM意味着缩减状态机的状态数目，同时保证状态机能实现同样功能。一种可能是使用真值表或Moore简约过程。另一种可能是无环FSA的自底向上算法（页面存档备份，存于互联网档案馆）。

实现

硬件应用

在数字电路中，FSM可以用可编程逻辑设备、可编程逻辑控制器、逻辑门和触发器或继电器来建造。更明确的说，硬件实现要求寄存器来存储状态变量，确定状态转移的一块组合逻辑，和确定FSM输出的另一块组合逻辑。一类经典硬件实现是Richards 控制器。

软件应用

下列概念经常用来建造有有限状态机的软件应用：

參考文獻

^ Sipser, Introduction to the Theory of Computation (2006), p. 34

參考書目

Wagner, F., "Modeling Software with Finite State Machines: A Practical Approach", Auerbach Publications, 2006, ISBN 0-8493-8086-3.
Samek, M., Practical Statecharts in C/C++^{[永久失效連結]}, CMP Books, 2002, ISBN 1-57820-110-1.
Samek, M., Practical UML Statecharts in C/C++, 2nd Edition （页面存档备份，存于互联网档案馆）, Newnes, 2008, ISBN 0-7506-8706-1.
Cassandras, C., Lafortune, S., "Introduction to Discrete Event Systems". Kluwer, 1999, ISBN 0-7923-8609-4.
Timothy Kam, Synthesis of Finite State Machines: Functional Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
Tiziano Villa, Synthesis of Finite State Machines: Logic Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
Carroll, J., Long, D. , Theory of Finite Automata with an Introduction to Formal Languages. Prentice Hall, Englewood Cliffs, 1989.
Kohavi, Z., Switching and Finite Automata Theory. McGraw-Hill, 1978.
Gill, A., Introduction to the Theory of Finite-state Machines. McGraw-Hill, 1962.
Ginsburg, S., An Introduction to Mathematical Machine Theory. Addison-Wesley, 1962.

外部链接

Description from the Free On-Line Dictionary of Computing^{[永久失效連結]}
NIST Dictionary of Algorithms and Data Structures entry （页面存档备份，存于互联网档案馆）
Hierarchical State Machines （页面存档备份，存于互联网档案馆）
Round-trip Engineering State Machines
Using state machines in practical applications
Flash based demonstration of Finite State Machines being used in regular expressions
"Moore or Mealy model?" （页面存档备份，存于互联网档案馆）关于使用Moore和Mealy模型的区别的细节，包括执行例子

参见

[1] Sipser, Introduction to the Theory of Computation (2006), p. 34

[1]

数字电路
概念	数字信号布尔代数開關组合逻辑电路时序逻辑电路同步異步真值表卡诺图有限状态机米利机摩尔机
硬件模块	邏輯閘与或非同与非或非异或同或蘊含 TTL 74190 CMOS 加法器乘法器编码器译码器数据选择器锁存器寄存器触发器 RS D JK T 儲存裝置 ROM RAM 類比數位轉換器數位類比轉換器
IC、VLSI	定制程度（半、全） PLD PAL PLA GAL CPLD FPGA ASIC 设计验证电子设计自动化（EDA）硬件描述语言 Verilog VHDL 逻辑综合硬件验证语言 SystemVerilog