Histopathology image classification: Highlighting the gap between manual analysis and AI automation

Brzina svetlosti

Sunčevoj svjetlosti je potrebno oko 8 minuta i 17 sekundi da pređe prosečno rastojanje od površine Sunca do Zemlje.
Tačne vrednosti
metara u sekundi	Šablon:FormattingError
Plankova dužina po Plankovom vremenu (i.e., Plankove jedinice)	1
Aproksimativne vrednosti (do tri značajne cifre)
Kilometara na sat	Šablon:FormattingError milion (Šablon:FormattingError)
milja po sekundi	Šablon:FormattingError
milja po satu[1]	671 milion (Šablon:FormattingError)
astronomskih jedinica na dan	173[Note 1]
parseka godišnje	0,307[Note 2]
Aproksimativno vreme putovanja svetlosnog signala
Rastojanje	Vreme
jedna stopa	1,0 ns
jedan metar	3,3 ns
od geostacionarne orbite do Zemlje	119 ms
dužina Zemljinog ekvatora	134 ms
od Meseca do Zemlje	1,3 s
od Sunca do Zemlje (1 AU)	8,3 min
jedna svetlosna godina	1,0 godina
jedan parsek	3,26 godina
od najbliže zvezde do Sunca (1,3 pc)	4,2 godina
od najbliže galaksije (patuljaste galaksije Veliki pas) do Zemlje	Šablon:FormattingError
preko Mlečnog puta	Šablon:FormattingError
od galaksije Andromeda do Zemlje	2,5 miliona godina
od Zemlje do kraja vidljivog svemira	46,5 milijardi godina

Brzina svetlosti u vakuumu iznosi tačno 299.792.458 m/s (približno 300.000 km/s), predstavlja važnu fizičku konstantu i zato se obeležava posebnim slovom c. U različitim sredinama (tečnostima, gasovima itd.) brzina svetlosti je različita i uvek manja nego u vakuumu.^[2] S obzirom da je svetlost oblik elektromagnetnog zračenja, njena brzina zavisi od električnih i magnetnih svojstava sredine kroz koju se kreće i konstantna je za tu sredinu.^[3] Izračunava se na osnovu formule: . U vakuumu je .

Brzina svetlosti je jedan od važnijih pojmova u Ajnštajnovoj teoriji relativnosti. U teoriji relativnosti, c međusobno povezuje prostor i vreme, a isto tako se javlja u poznatoj jednačini jednakosti mase i energije E = mc².^[4] Prema istoj teoriji nije moguće kretanje brzinama većim od brzine svetlosti u vakuumu.^[5]

Prvu poznatu naučnu metodu za merenje brzine svetla izveo je danski astronom Ole Kristensen Remer 1675. godine. Posle njega, Fizo bez astronomskih metoda dolazi do brzine svetlosti koja iznosi 313.870 km/s. Najpoznatije merenje brzine je izveo Albert Majkelson, uz pomoć rotirajućih ogledala u Kaliforniji. Zahvaljujući tim eksperimentima, utvrđeno je da je brzina svetlosti 299.792,458 km/s, a sam Majkelson je dobio Nobelovu nagradu 1907.

S obzirom da se osnovna merna jedinica za vreme, sekunda, može preciznije izmeriti od osnovne jedinica za dužinu, metra, brzina svetlosti je iskorišćena za preciznu definiciju ove merne jedinice. Tako je od 21. oktobra 1983. godine metar određen kao rastojanje koje svetlost pređe u vakuumu za 1/299.792.458 deo sekunde.^[6]

Brzina svetlosti u vakuumu se obično označava malim slovom c, za constant ili lat. celeritas (sa značenjem „brzina“). Istorijski, simbol V je korišten kao alternativni simbol za brzinu svetlosti, koji je uveo Džejms Klerk Maksvel 1865. godine. Pol Drud je 1894. godine redefinisao simbol c u njegovo sadašnje značenje. Ajnštajn je koristio V u svojim originalnim publikacijama na nemačkom o specijalnoj relativnosti 1905, ali je 1907. prešao na c, koje je u to vreme postalo standardni simbol za brzinu svetlosti.^[7][8]

Ponekad se c koristi za brzinu talasa u bilo kom materijalnom mediju, a c₀ za brzinu svetlosti u vakuumu.^[9] Ova usvojena notacija, koja je podržana u zvaničnoj SI literaturi,^[6] ima istu formu kao i druge srodne konstante: naime, μ₀ za permeabilnost vakuuma ili magnetna konstanta, ε₀ za dielektričnu konstantu vakuuma ili električnu konstantu, i Z₀ za otpornost prostora. Ovaj članak isključivo koristi c za brzinu svetlosti u vakuumu.

Od 1983, metar je definisan u Međunarodnom sistemu jedinica (SI) kao rastojanje koje svetlost pređe u vakuumu za ¹⁄_{Šablon:FormattingError} sekundi. Ova definicija podrazumeva brzinu svetlosti u vakuumu na tačno Šablon:FormattingError.^[10][11][12] Kao dimenziona fizička konstanta, numerička vrednost c se razlikuje za različite sisteme jedinica. Brzina svetlosti u imperijalnim (britanskim) jedinicama i SAD jedinicama je bazirana na inču sa tačno Šablon:FormattingError i njena vrednosti je tačno 186.282 milja, 698 jardi, 2 stope, i 5+²¹⁄₁₂₇ inča po sekundi.^[13] U granama fizike u kojima se c često javlja, kao što je teorija relativnosti, uobičajeno se koriste sistemi prirodnih jedinica kretanja ili geometrijski sistem jedinica gde c = 1.^[14][15] Koristeći ove jedinice, c se ne pojavljuje eksplicitno pošto množenje ili deljenje sa 1 ne utiče na rezultat.

Pre prvih naučnih pokušaja merenja brzine svetlosti, najveće rasprave su se vodile oko toga putuje li svetlost konačnom brzinom, ili se širi prostorom trenutno (beskonačno brzo). Više fizičara je pokušalo da izmeri brzinu svetlosti kroz istoriju. Galileo je pokušao da to uradi u sedamnaestom veku.

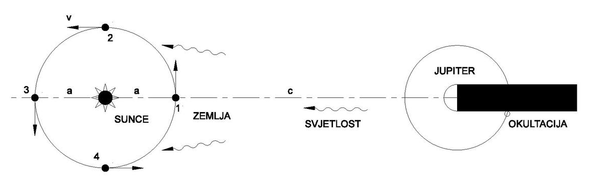
Danski astronom Ole Rømer je izveo rani eksperiment merenja brzine svetlosti 1676. godine. Koristeći teleskop, Rømer je posmatrao kretanje Jupitera i jednog od njegovih satelita, Io. Uočivši odstupanja u uočenom periodu Iove orbite, on je izračunao da je svetlosti potrebno oko 22 minuta da pređe dijametar Zemljine orbite.^[16] On je ustanovio da trenuci opažanja okultacija (kad se nebesko telo, gledano sa Zemlje, skriva iza drugog) Jupiterovih satelita zavise od brzine širenja svetlosti. Do tada se smatralo da se svetlost širi beskonačnom brzinom. Kada se Zemlja nalazi u položaju 1. (vidi sliku), posmatrač uočava da do okultacija dolazi u jednakim vremenskim razmacima, tada se Zemlja niti približava niti udaljava od Jupitera. U položaju 2. Zemlja se udaljava od Jupitera, a posmatrač nalazi da trenuci okultacije kasne. Razlog je u tome što je svetlosti potrebno dodatno vreme da prevali povećanu udaljenost do Zemlje. Znajući u kojim su se razmacima vremena okultacije pojavljivale u položaju 1, može se predvideti vreme okultacije kada se dođe u položaju 3. Međutim do nje ne bi dolazilo još toliko vremena koliko je svetlosti potrebno da prevali udaljenost od položaja Zemlje 1. do položaja Zemlje 3, a to je dužina 2a. Remer je izmerio da ukupno kašnjenje iznosi oko t = 1,000 sekundi. Za brzinu svetlosti sledi:^[17]

gde je: c – brzina svetlosti, a – udaljenost Zemlje od Sunca, t – vreme kašnjenja svetlosti.

Brojna vrednost brzine svetlosti direktno zavisi od tačnosti s kojom je poznata srednja udaljenost do Sunca (u ono vreme poznata kao 140 milona kilometara). Odnos brzine svetlosti i brzine Zemlje ne zavisi od srednje udaljenosti do Sunca. Naime, kako je brzina kretanja Zemlje po stazi jednaka v = 2aπ / Z, gde je Z siderička godina, to je:

gde je: c – brzina svetlosti, v = brzina kretanja Zemlje, a – udaljenost Zemlje od Sunca, Z - siderička godina Zemlje, π = 3.14, t – vreme kašnjenja svetlosti.

Remer je vršio merenja oko 8 godina i odnos c : v je izašao oko 7600. No veličina Zemljine orbite nije bila poznata u to vreme. Na osnovu njegovih merenja brzinu svetlosti je izračunao Kristijan Hajgens i on je dobio za oko 25% manju vrednost od današnjih merenja, odnosno 227.000.000 m/s. Današnje vrednosti su 299.792 km/s : 29,8 km/s ≈ 10,100.

Značajno je da je Remer dokazao da je brzina svetlosti konačna. Njegovi rezultati nisu u početku prihvaćeni, sve dok Džejms Bredli 1727. nije otkrio aberaciju svetlosti.

Godine 1809. francuski astronom Žan-Batist-Žozef Delambr je ponovio Remerova merenja, koja su tada obavljena s mnogo tačnijim mernim instrumentima i dobio za brzinu svetlosti oko 300.000 km/s. On je u stvari izmerio da svetlost putuje sa Sunca do Zemlje 8 minuta i 12 sekundi (stvarna vrednost je 8 minuta i 19 sekundi).

Pored astronomskih merenja, naučnici su pokušali da mere brzinu svetlosti na Zemlji, na relativno malim udaljenostima. Ipolit Fizo je 1849. godine izveo jedno takvo merenje. On je usmerio zrak svetlosti u ogledalo udaljeno nekoliko kilometara. Rotirajući zupčanik je postavljen na putu svetlosnog zraka koji se kretao od njegovog izvora do ogledala i nazad. Fizo je utvrdio da pri određenoj brzini rotacije, zrak prolazi kroz jedan otvor na zupčaniku na svom putu ka ogledalu i kroz sledeći otvor na povratku. Polazeći od rastojanja do ogledala, broja zuba na zupčaniku, i brzine rotacije, Fizo je dobio brzinu svetlosti od oko 313.300 km/s.

Leon Fuko je 1862. godine izvršio eksperiment u kome su korišćena rotirajuća ogledala i došao je do vrednosti od 298.000.000 m/s.

Američki fizičar Albert Abraham Majkelson je sprovodio eksperimente određivanja brzina svetlosti od 1877. do svoje smrti 1931. Koristio se osmostaničnim rotirajućim ogledalom i izvorom svetlosti udaljenim oko 35 km. On je rafinirao Fukove metode 1926. godine koristeći poboljšana rotirajuća ogledala da izmeri vreme neophodno da svetlost napravi povratno putovanje od Mount Wilson do Mount San Antonio u Kaliforniji. Precizna merenja su proizvela vrednost brzine od 299.796,000 m/s.^[18] Za svoja je merenja svetlosti primio Nobelovu nagradu za fiziku. Posle je s kolegom Edvardom Morlejem sproveo Majkelson—Morlijev eksperiment, u kojem su dokazali da brzina svetlosti ne zavisi od izvora, niti od brzine kretanja izvora.

Savremena merenja su utvrdila brzinu svetlosti na tačno 299.792.458 m/s.

Efektivna brzina svetlosti u raznim transparentnim supstancama je manja od brzine u vakuumu. Na primer brzina svetlosti u vodi je oko 3/4 brzine u vakuumu.

Dva nezavisna tima fizičara su dovela svetlost u „kompletan zastoj“ propuštajući je kroz Bose–Ajnštajnov kondenzat elementa rubidijuma. Jedan tim je bio sa Harvarda i Roulandovog instituta za nauku u Kambridžu, Masačusets, a drugi sa Harvard–Smitsonijanskog centra za astrofiziku, takođe u Kembridžu.^[19] Međutim, taj „zastoj“ se odnosi samo na zastavljanje svetlosti u pobuđenim stanjima atoma, i njeno reemitovanje nakon arbitrarnog vremenskog razmaka, nakon stimulacije drugim laserskim pulsom. Tokom vremena u kome je svetlost bila „zaustavljena“, ona je prestala da bude svetlost.

Glavni članak: Granična brzina

Prema posebnoj teoriji relativnosti, energija predmeta mase m i brzine v data je jednačinom γmc², gde je γ Lorencov faktor. Ako telo miruje, v je jednaka nuli, pa je γ jednak 1, iz čega sledi E = mc², kojim se definiše ekvivalencija mase i energije. γ se približava beskonačnosti kako se v približava c, pa bi bila potrebna beskonačna količina energije kako bi objekt mase m dostigao brzinu svetlosti. Drugim rečima, masa m tela koje miruje manja je od mase m₀ tela koje se kreće: u skladu sa formulom . To znači da što je telo brže, i što se više približava brzini svetlosti, treba mu sve više energije kako bi svoju, sve veću masu, uspelo da ubrza. Brzina svetlosti je time gornja granica brzine za objekte koji posjeduju masu, pa zbog toga pojedinačni fotoni ne mogu putovati brzinama većim od brzine svetlosti.^[20][21] Ovo je eksperimentalno dokazano u mnogim testiranjima relativističke energije i momenta.^[22]

• Stachel, JJ (2002). Einstein from "B" to "Z" – Volume 9 of Einstein studies. Springer. str. 226. ISBN 978-0-8176-4143-6. 
• Larson, Ron; Hostetler, Robert P. (2007). Elementary and Intermediate Algebra: A Combined Course, Student Support Edition (4th illudtrated izd.). Cengage Learning. str. 197. ISBN 978-0-618-75354-3. 
• Rømer, O (1676). „Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Academie Royale des Sciences” (French). Journal des sçavans: 223–36. Arhivirano iz originala na datum 29. 7. 2007. 
• Halley, E (1694). „Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London”. Philosophical Transactions of the Royal Society 18 (214): 237–56. DOI:10.1098/rstl.1694.0048. 
• Foucault, JL (1862). „Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil” (French). Comptes rendus de l'Académie des sciences 55: 501–503,792–796. 
• Michelson, AA (1878). „Experimental Determination of the Velocity of Light”. Proceedings of the American Association of Advanced Science 27: 71–77. 
• Michelson, AA; Pease, FG; Pearson, F (1935). „Measurement of the Velocity of Light in a Partial Vacuum”. Astrophysical Journal 82: 26–61. Bibcode 1935ApJ....82...26M. DOI:10.1086/143655. 
• Newcomb, S (1886). „The Velocity of Light”. Nature 34 (863): 29–32. Bibcode 1886Natur..34...29.. DOI:10.1038/034029c0. 
• Perrotin, J (1900). „Sur la vitesse de la lumière” (French). Comptes rendus de l'Académie des sciences 131: 731–4. 
• Brillouin, L (1960). Wave propagation and group velocity. Academic Press. 
• Jackson, JD (1975). Classical Electrodynamics (2nd izd.). John Wiley & Sons. ISBN 978-0-471-30932-1. 
• Keiser, G (2000). Optical Fiber Communications (3rd izd.). McGraw-Hill. str. 32. ISBN 978-0-07-232101-2. 
• Ng, YJ (2004). „Quantum Foam and Quantum Gravity Phenomenology”. u: Amelino-Camelia, G. Planck Scale Effects in Astrophysics and Cosmology. Springer. str. 321ff. ISBN 978-3-540-25263-4. 
• Helmcke, J; Riehle, F (2001). „Physics behind the definition of the meter”. u: Quinn, TJ. Recent advances in metrology and fundamental constants. IOS Press. str. 453. ISBN 978-1-58603-167-1. 
• Duff, MJ (2004). „Comment on time-variation of fundamental constants”. arXiv:hep-th/0208093 [hep-th]. 

Brzina svjetlosti na Wikimedijinoj ostavi

• Svetlost