Histopathology image classification: Highlighting the gap between manual analysis and AI automation
فهرست
-
بخش آغازین
-
۱ مشتق تابع
-
۲ نمادهای مشتق
-
۳ مشتقهای یک طرفه
-
۴ مشتقپذیری
-
۵ دامنهٔ تابع مشتق
-
۶ مشتق تابع نسبت به تابع
-
۷ مشتق مراتب بالاتر
-
۸ قضیهٔ رول
-
۹ قضیهٔ لاگرانژ
-
۱۰ قضیهٔ کوشی
-
۱۱ کاربرد مشتق
-
۱۲ قواعد مشتقگیری
-
۱۳ جستارهای وابسته
-
۱۴ منابع
-
۱۵ پیوند به بیرون
| بخشی از سری مقالات |
| حسابان |
|---|

| بخشی از سری مقالات |
| حسابان |
|---|
مشتق (به انگلیسی: Derivative) ایدهٔ اصلی حساب دیفرانسیل، بخش اول آنالیز ریاضی است که نرخ تغییرات تابع را نشان میدهد. مشتق نیز، نظیر انتگرال، از مسئلهای در هندسه، یعنی یافتن خط مماس در یک نقطه از منحنی ناشی شدهاست.
عملیات مشتق گیری همانند یا شبیه دیفرانسیل گیری و برعکس عملیات انتگرال گیری است.
در نگاه نخست اینطور به نظر میرسید که بین مسئلهٔ یافتن مساحت سطح زیر یک نمودار و موضوع تعیین خط مماس بر منحنی در یک نقطه رابطهای وجود ندارد، اما اولین کسی که دریافت این دو مفهومِ به ظاهر دور از هم، در واقع ارتباط نسبتاً نزدیکی با هم دارند آیزاک بارو معلم آیزاک نیوتون بودهاست.
اما مفهوم مشتق به شکل امروزی آن، نخستین بار در سال ۱۶۶۶ میلادی توسط نیوتون و به فاصلهٔ چند سال بعد از او، توسط گوتفرید لایبنیتس، مستقل از یکدیگر پدید آمد. این دو دانشمند در ادامهٔ کار خود، باز هم بهطور مستقل، بخش دوم آنالیز ریاضی یعنی حساب انتگرال را عرضه کردند که اساس آن بر عمل انتگرالگیری قرار دارد.
نیوتون از شیوهٔ استدلال سینماتیک و با دیدگاه فیزیکی به بررسی مشتق پرداخته و از آن برای بدست آوردن سرعت لحظهای استفاده میکرد. اما لایبنیتس با دیدگاهی هندسی، از مشتق برای بدست آوردن ضریب زاویهٔ مماس در منحنیها استفاده میکرد. هر یک از این دو دانشمند نمادهای جداگانهای را برای نشان دادن مشتق به کار میبردند.[۱][۲]
پیشرفت حساب دیفرانسیل و انتگرال در دوران بعد به آگوستَن لویی کوشی، برنهارد ریمان و برادران برنولی، یعنی یاکوب و یوهان، مربوط میشود. گیوم لوپیتال (به فرانسوی: Guillaume de l'Hôpital)، دانشمند فرانسوی، در سال ۱۶۹۶ نخستین کتاب درسی مربوط به آنالیز ریاضی را با نام «آنالیز بینهایت کوچکها برای بررسی منحنیها» منتشر کرد که در واقع خلاصهای از درسهایی بود که یوهان برنولی به عنوان معلم برای او نوشته بود. در این کتاب، قاعدهٔ رفع ابهام در حد، با استفاده از مشتق نیز آمده که به قاعدهٔ هوپیتال مشهور است ولی در واقع متعلق به یوهان برنولی بودهاست.
مشتق تابع
اگر نقطهای از نمودار تابع و نقطهٔ دیگری از این نمودار باشد، آنگاه و شیب خط قاطع عبارت است از:
کسر فوق، خارج قسمت تفاضلی در نامیده میشود. اگر ثابت نگه داشته شود و به سمت صفر میل کند، آنگاه خارج قسمت تفاضلی در اگر فقط به بستگی داشته باشد به مقداری میل میکند که به آن شیب خط مماس گفته میشود. به عبارت دیگر، حاصل حد زیر در صورت وجود ضریب زاویهٔ خط مماس نمودار تابع در را بدست میدهد:
تعریف مشتق تابع
برای تابع که در همسایگی نقطهٔ تعریف شدهاست، اگر وجود داشته باشد، در مشتقپذیر است. این حد (ریاضی) یکتا را با نمایش داده و آن را مشتق تابع در نقطهٔ مینامند.
بر طبق این تعریف، مقدار مشتق برابر نرخ تغییرات مقدار تابع است زمانی که تغییرات مربوط به متغیر مستقل به سمت صفر میل میکند.[۳]
با تبدیل به تعریف دوم مشتق به صورت زیر حاصل میشود:
نمادهای مشتق
لایبنیتس، نیوتون، لاگرانژ، آربوگاست و اویلر هر یک نماد جداگانهای را برای نمایش مشتق بکار میبردند؛ اما در میان پیشگامان اولیهٔ آنالیز ریاضی، لایبنیتس بیش از هر کس دیگری به اهمیت علامات مناسب پی برده بود. او علامات را با حوصلهٔ زیادی آزمایش میکرد و با سایر ریاضیدانان مکاتبات بسیاری داشت و از این طریق معایب و محاسن نمادهای مختلف را برای آنها مطرح میساخت. پیشرفت حساب دیفرانسیل و انتگرال و گسترش ریاضیات نوین تا حدود زیادی بواسطهٔ علامتهای پیشرفتهای است که بسیاری از آنها توسط لایبنیتس ابداع شدهاند.
لایبنیتس در سال ۱۶۷۵ میلادی با استفاده از عملگر تفاضلی خارج قسمت تفاضلی را به شکل نوشت و برای مشتق تابع در نماد را معرفی کرد که به صورت نیز نوشته میشود. این نماد که نمایش دیفرانسیلی مشتق نامیده میشود، برای نمایش مشتق مراتب بالاتر به شکل نوشته میشود. با استفاده از این نماد تعریف مشتق به صورت در میآید.
نیوتون برای نشان دادن مشتق اول از و برای مشتق دوم از استفاده میکرد. نمادهای نقطهدار نیوتون در برخی مسائل فیزیکی مانند سرعت و شتاب بکار میروند.
مشتق تابع را با نیز میتوان نشان داد. این نماد بر آن تأکید دارد که تابع جدیدی است که با مشتقگیری از تابع بدست آمدهاست و مقدارش در با نموده میشود. مختصات و واقع بر نمودار با معادلهٔ به هم مربوط میشوند، و علامت نیز برای نمایش بکار میرود که مقدارش در به صورت نوشته میشود. این نماد در سال ۱۷۷۰ میلادی توسط ژوزف لویی لاگرانژ مورد استفاده قرار گرفت و مشتق مراتب بالاتر را به صورت (مشتق اول)، (مشتق دوم)، (مشتق سوم)، (مشتق چهارم) … (مشتق ام) نشان میدهد.
در سال ۱۸۰۰ میلادی نماد دیگری توسط لوییس آربوگاست معرفی شد و توسط لئونارد اویلر مورد استفاده قرار گرفت. این نماد مشتق را به شکل نشان میدهد. علامت یک عملگر دیفرانسیلی است و این فکر را القا میکند که تابع جدیدی است که با مشتقگیری از بدست آمدهاست. مشتق مراتب بالاتر به صورت و مقدار آن در به صورت نوشته میشود.[۴]
مشتقهای یک طرفه
مشتق راست: اگر تابع در فاصلهٔ تعریف شده باشد آنگاه حاصل حد زیر، در صورت وجود، مشتق راست تابع در میباشد:
|
|
مشتق چپ: اگر تابع در فاصلهٔ تعریف شده باشد آنگاه حاصل حد، زیر در صورت وجود، مشتق چپ تابع در میباشد:
|
|
مشتقپذیری

تابع در مشتقپذیر است هرگاه در این نقطه پیوسته باشد و مشتق چپ و راست تابع با هم برابر و مساوی یک عدد حقیقی معین باشد.
تعبیر هندسی مشتقپذیری: تابع در مشتقپذیر است هرگاه بتوان در این نقطه یک خط کامل مماس و غیر موازی با محور yها بر منحنی رسم کرد.
اگر تابع در نقطهٔ مشتقپذیر باشد، آنگاه در آن نقطه پیوسته نیز هست.
ولی عکس قضیهٔ فوق صحیح نمیباشد یعنی ممکن است تابع پیوسته باشد اما مشتقپذیر نباشد؛ به عبارت دیگر، پیوستگی تابع در شرط لازم برای مشتقپذیری تابع است، نه شرط کافی. پس اگر تابع در ناپیوسته باشد، آنگاه در مشتقپذیر نیست.[۶]
موارد مشتقناپذیری

مواردی که تابع در نقطهٔ مفروض مشتقپذیر نیست:
- نقاط ناپیوسته: تابع در نقاط ناپیوسته مشتقناپذیر است و از دید هندسی نمیتوان در این نقاط مماس بر منحنی رسم کرد.
- نقاط زاویهدار: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها دو عدد حقیقی نابرابر، یا یکی عدد و دیگری بینهایت باشد، مشتقپذیر نیست. از دید هندسی، در این نقاط دو نیممماس بر منحنی رسم میشود که با هم زاویه میسازند.
- نقاط عطف قائم: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها بینهایتهای همعلامت باشد مشتقناپذیر است. از دید هندسی، در این نقاط میتوان یک خط کامل مماس به موازات محور yها رسم کرد. نقطهٔ عطف قائم تنها نقطهای است که تابع در آن مشتقپذیر نیست ولی مماس کامل دارد.
- نقاط بازگشت: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها بینهایتهای غیر همعلامت باشد مشتقناپذیر است. از دید هندسی، در این نقاط میتوان یک نیممماس، به موازات محور yها رسم کرد.
- تابع در نقاطی که پیوستهاند ولی مشتق در آنها به سمت عدد مشخصی میل نمیکند نیز مشتقناپذیر است. از دید هندسی، در این نقاط نمیتوان مماس مشخصی بر منحنی رسم کرد.
دامنهٔ تابع مشتق
منظور از دامنهٔ تابع مشتق مجموعهٔ نقاطی است که تابع در آنها مشتقپذیر است. بهطور کلی برای تابع داریم:
- مجموعه نقاطی که در آن تعریف نشدهاست
مشتق تابع نسبت به تابع
هرگاه بخواهیم انتگرال یک تابع مانند را نسبت به تابع دیگری مانند بدست آوریم، کافی است مشتق این توابع را نسبت به متغیرشان محاسبه نموده و سپس برهم تقسیم کنیم.
مشتق توابع پارامتری
توابع که به فرم هستند را توابع پارامتری مینامند. در این حالت، مشتق نسبت به از رابطهٔ زیر قابل محاسبه است:
مشتق تابع مرکب
اگر تابع در نقطهٔ و تابع در مشتقپذیر باشد، آنگاه تابع نیز در مشتقپذیر است و داریم:
به بیان دیگر، هرگاه تابعی از و تابعی از باشد، برای بدست آوردن مشتق نسبت به ، مشتق نسبت به را در مشتق نسبت به ضرب میکنیم.
همچنین به شکل دیگری برای توابع ، و داریم:
مشتق توابع زوج و فرد
مشتق هر تابع زوج، تابعی فرد است و مشتق هر تابع فرد، تابعی زوج است.
اگر تابعی زوج و موجود نباشد ولی و موجود باشند آنگاه خواهیم داشت:
اگر تابعی فرد و موجود نباشد ولی و موجود باشند آنگاه خواهیم داشت:
پادمشتق
اگر تابعی پیوسته در بازهٔ شامل نقطهٔ باشد، آنگاه تابع با دامنهٔ و با ضابطهٔ:
تابع اولیه یا پادمشتق تابع نامیده میشود. تابع روی مشتقپذیر است و برای هر داریم:
اگر آنگاه مشتق تابع از رابطهٔ زیر بدست میآید:
مشتق جزئی
مشتق جزئی، پارهای یا نسبی، به مشتق تابع چند متغیرهٔ نسبت به یکی از متغیرها با ثابت در نظر گرفتن سایر متغیرها گفته میشود. مشتق جزئی را به جای با نمایش میدهند که «دِل»، «دِر» یا «پارشال» خوانده میشود. برای مثال، مشتق جزئی تابع نسبت به به صورت زیر نوشته میشود:
بهطور کلی، حاصل حد زیر، در صورت وجود برابر مشتق جزئی تابع چند متغیرهٔ نسبت به در است:
|
|
مشتق ضمنی
در مقابل رابطهٔ صریح تابع به شکل کلی ، رابطهٔ ضمنی آن به صورت قرار میگیرد. برای محاسبهٔ مشتق توابع ضمنی دو روش کلی وجود دارد:
- استفاده از قاعدهٔ زنجیری: در این روش، از طرفین رابطه نسبت به مشتق میگیریم و با فاکتورگیری، را بدست میآوریم. (اگر بخواهیم مشتق را نسبت به حساب کنیم آنگاه و خواهد بود)
- استفاده از مشتق جزئی: در این روش از رابطهٔ زیر استفاده میشود:
مشتق جهتدار
مشتق جزئی تابع میزان تغییرات را در امتداد محورهای مختصات به دست میدهد در حالیکه مشتق جهتدار، سویی یا جهتی، میزان تغییرات را در امتداد یک بردار دلخواه در فضا حساب میکند. اگر در همسایگی نقطهٔ تعریف شده باشد و برداری شامل نقطهٔ باشد، مشتق جهتدار در به صورت زیر محاسبه میشود:
|
|
که در آن نقطهٔ باید متعلق به باشد و فاصلهٔ علامتدار تا است یعنی اگر و همجهت باشند و در غیر این صورت در نظر گرفته میشود.
مشتق تابع برداری
مشتق تابع برداری با فرض اینکه مؤلفههای سمت راست بامعنی باشند، به صورت زیر تعریف میشود:
|
|
تابع بر بازهٔ پیوسته و مشتقپذیر است، هرگاه تک تک مؤلفههای بر بازهٔ پیوسته و مشتقپذیر باشند. با توجه به این تعریف، بسیاری از قضایای مشتق توابع حقیقی برای توابع برداری نیز صادقاند.
برای محاسبهٔ مشتق یک تابع برداری، میتوان آن را برحسب مؤلفههای قائم خود، به صورت و نوشت و از هر کدام بهطور جداگانه مشتق گرفت؛ یعنی اگر و وجود داشته باشند مشتق تابع برداری به صورت زیر نوشته میشود:
|
|
مشتق کل
هرگاه تابعی از به باشد، آنگاه مشتق جهتدار در یک جهت بخصوص، بهترین تقریب خطی در آن نقطه و جهت است. اما هرگاه باشد، دیگر مشتق جهتدار نمیتواند به تنهایی، تصویر کاملی از رفتار تابع نشان دهد. مشتق کل، که دیفرانسیل کل نیز نامیده میشود با در نظر گرفتن رفتار تابع در تمام جهتها میتواند تصویر کاملی از رفتار تابع ارائه کند.
برخلاف مشتق جزئی، در محاسبهٔ مشتق کل تابع نسبت به متغیر ، متغیرهای دیگر ثابت در نظر گرفته نمیشوند بلکه به بستگی خواهند داشت و مشتق کل به صورت زیر تعریف میشود:
مشتق کل در حساب دیفرانسیل با مفهومی مشابه، به یک عملگر دیفرانسیلی نیز گفته میشود. این عملگر دیفرانسیلی، مشتق کل تابع را نسبت به صورت زیر محاسبه میکند:
مشتق تابع معکوس

اگر تابع در همسایگی نقطهٔ پیوسته و یک به یک بوده و موجود و غیر صفر باشد، آنگاه تابع در نقطهٔ مشتقپذیر است و داریم:
تعبیر هندسی: شیب خط مماس بر منحنی در نقطهٔ برابر است با عکس شیب خط مماس بر منحنی در نقطهٔ . (نقاط و متناظر هستند)
از قضیهٔ مشتق تابع معکوس، روابط زیر را نیز خواهیم داشت:
|
|
مشتق مراتب بالاتر
اگر تابع روی بازهٔ مشتقپذیر باشد تابع خود ممکن است در نقطهای مثل مشتقپذیر باشد. به عبارتی اگر موجود باشد، میگوییم مشتق مرتبهٔ دوم تابع در موجود است و آن را با نمایش میدهیم.
مشتق مراتب بالاتر یک تابع، از تعریف اصلی مشتق بدست میآید. بهطوریکه با مشتق گرفتن از مشتق اول تابع به مشتق دوم آن میرسیم و به همین ترتیب مشتق مراتب بالاتر نیز تعریف میشوند. به صورت کلی داریم:
مشتق nام چند تابع مهم
مشتق ام چند تابع مهم نسبت به که و اعداد ثابت هستند:
|
|
قاعدهٔ لایبنیتس
قاعدهٔ لایبنیتس بیان میکند که اگر دو تابع و روی بازهٔ دارای مشتقهای متوالی تا مرتبهٔ باشند، آنگاه حاصلضرب نیز روی این بازه دارای مشتقهای متوالی تا مرتبهٔ است و داریم:
|
|
قضیهٔ رول
اگر تابع روی پیوسته، روی بازهٔ مشتقپذیر و باشد آنگاه حداقل یک نقطهٔ در بازهٔ وجود دارد که در آن است. عدد با خاصیت فوق منحصر به فرد نیست و باید یک نقطهٔ درونی بازهٔ باشد.
نقاط در قضیهٔ رول نقاطی هستند که مماس بر نمودار در آنها خطوط افقی است، یعنی قضیهٔ رول شرایط وجود مماس افقی را برآورد میکند.
نتیجهٔ قضیهٔ رول: اگر تابع روی پیوسته باشد و آنگاه حداقل یک نقطهٔ اکسترمم نسبی در بازهٔ وجود دارد.
حالت خاص قضیهٔ رول: اگر فرض کنیم با استفاده از قضیهٔ رول میتوان گفت که بین هر دو ریشهٔ تابع مشتقپذیر مشتقِ تابع یعنی حداقل یک ریشه دارد.[۷]
قضیهٔ لاگرانژ
قضیهٔ لاگرانژ یا مقدار میانگین مشتق بیان میکند که هرگاه تابع روی پیوسته و روی بازهٔ مشتقپذیر باشد، آنگاه حداقل یک نقطهٔ در بازهٔ وجود دارد که در آن:
- تعبیر هندسی: قضیه بیان میکند که در بازهٔ حداقل یک نقطه وجود دارد که مماس بر منحنی در آن نقطه به موازات خط واصل نقاط دو سر منحنی است.
- تعبیر فیزیکی: اگر نمودار را مکان-زمان در نظر بگیریم و بازهٔ بازهٔ زمانی باشد، قضیهٔ فوق میگوید، حداقل یک لحظه در بازهٔ وجود دارد که سرعت لحظهای با سرعت متوسط برابر میشود.که این لحظه برابر است با لحظه وسط بازه.
قضیهٔ کوشی
قضیهٔ کوشی که صورت تعمیم یافتهٔ قضیهٔ لاگرانژ است، بیان میکند که هرگاه توابع و روی بازهٔ پیوسته و روی بازهٔ مشتقپذیر باشند، آنگاه حداقل یک نقطهٔ در بازهٔ وجود دارد که در آن:
کاربرد مشتق
خط مماس و قائم
مشتق به ازای مختصات نقطهٔ تماس برابر است با ضریب شیب خط مماس. پس برای تعیین شیب خط مماس یا قائم بر منحنی و تعیین معادلهٔ آنها میتوان از مشتق استفاده کرد.

معادلهٔ خط مماس در نقطهٔ واقع بر منحنی:
معادلهٔ خط قائم در نقطهٔ واقع بر منحنی:

معادلهٔ خط مماس بر منحنی از نقطهای خارج از منحنی: اگر بخواهیم از نقطهٔ مماسی بر منحنی رسم کنیم، نقطهٔ تماس را در نظر میگیریم، چون نقطهٔ روی منحنی قرار گرفته از منحنی مشتق میگیریم و مختصات را قرار میدهیم تا شیب معادله بدست آید.
در نهایت چون نقطهٔ روی خط مماس قرار دارد، در معادلهٔ فوق قرار داده تا یک معادلهٔ یک مجهولی بر حسب بدست آید.
آهنگ تغییر
نسبت تغییرات دو کمیت را آهنگ تغییر یکی نسبت به دیگری میگویند.
آهنگ تغییر متوسط
آهنگ متوسط تغییرات در فاصلهٔ عبارت است از:
آهنگ متوسط تغییرات نسبت به متغیر عبارت است از:
آهنگ تغییر لحظهای
اگر تغییرات نسبت به تغییرات را آهنگ آنی (لحظهای) تغییر نسبت به گویند.
کمیتهای وابسته

در برخی موارد دو کمیت (متغیر)، علاوه بر اینکه به هم مربوطاند، هر دو به متغیر سومی که معمولاً زمان است، بستگی دارند. در این موارد آهنگ تغییر این دو کمیت، نسبت به کمیت سوم در نظر گرفته میشود. به عنوان مثال، حد تغییرات مسافت پیموده شده به تغییرات زمانی را سرعت لحظهای گویند:
|
|
زاویهٔ بین دو تابع
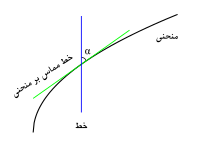
زاویهٔ بین خط و منحنی
زاویهٔ بین یک خط و منحنی عبارت است از زاویهٔ بین مماس رسم شده بر منحنی در نقطهٔ تقاطع با خط. برای تعیین زاویهٔ بین خط و منحنی به ترتیب زیر عمل میکنیم:
- خط را با منحنی قطع داده و مختصات نقطهٔ تقاطع را بدست میآوریم.
- از منحنی مشتق گرفته و ضریب زاویهٔ خط مماس بر منحنی را در نقطهٔ تقاطع مییابیم.
- با کمک رابطهٔ زاویهٔ بین خط مماس و منحنی را بدست میآوریم.
زاویهٔ بین دو منحنی
برای یافتن زاویهٔ بین دو منحنی، ابتدا آنها را با هم تلاقی داده و طول نقطهٔ تلاقی را مییابیم. سپس از دو منحنی مشتق گرفته و ضریب زاویههای بدست آمده را در رابطهٔ قرار میدهیم تا زاویهٔ بین دو منحنی بدست آید.
نقاط بحرانی
نقطهٔ درونی را نقطهٔ بحرانی تابع گویند هرگاه یا موجود نباشد. ریشههای مشتق، نقاط بازگشتی، زاویهدار، ناپیوستگی و عطف قائم، همگی جزو نقاط بحرانی تابع محسوب میشوند و نقاط ابتدا و انتها بازه به دلیل اینکه نقاط درونی بازه نیستند جزو نقاط بحرانی محسوب نمیشوند.
در ضمن، اگر تابع روی تعریف شده باشد و نقطهٔ درون این بازه، اکسترمم مطلق تابع روی این بازه باشد، آنگاه نقطهٔ بحرانی است. هر نقطهٔ اکسترمم نسبی نقطهٔ بحرانی نیز هست، در صورتیکه یک نقطهٔ بحرانی ممکن است نقطهٔ اکسترمم نسبی نباشد.
اگر تابع روی بازهٔ پیوسته باشد برای بدست آوردن مقادیر و مطلق ابتدا نقاط بحرانی را در بازه مشخص کرده و در تابع اصلی قرار میدهیم سپس و را نیز بدست میآوریم و با مقایسهٔ اعداد بدست آمده، اگر کمترین یا بیشترین مقدار مربوط به حدهای فوق باشد تابع فاقد یا مطلق است. در غیر این صورت یا مطلق را مشخص میکنیم.
اگر در بازهٔ فوق نقطهای مثل وجود داشته باشد که تابع در آن نقطه ناپیوسته باشد، میبایست و را نیز بدست آورد و مانند موارد بالا وجود یا را بررسی کرد.[۱۱]
تشخیص یکنوایی تابع
در تابع پیوستهٔ ، برای هر اگر آنگاه روی صعودی اکید است و اگر آنگاه روی نزولی اکید است؛ ولی اگر باشد، تابع صعودی غیر اکید است و اگر باشد، تابع نزولی غیر اکیداست
در این حالت برای تشخیص اکید یا غیر اکید بودن تابع ریشههای مشتق را بدست میآوریم، اگر ریشههای مشتق، تمام نقاط روی یک بازه باشند، تابع صعودی غیر اکید است و در غیر این حالت صعودی اکید است.
اگر تابع پیوسته نباشد، دامنهٔ تابع را به فاصلههایی که تابع در آنها پیوستهاست، تقسیم میکنیم و به کمک مشتق وضعیت یکنوایی تابع را در هر بازه مشخص میکنیم. سپس نقاط انتهایی هر بازه (یا حد انتهایی هر بازه) را با نقاط ابتدایی بازهٔ بعد (یا حد ابتدایی بازهٔ بعد) مقایسه میکنیم.
آزمونهای مشتق
آزمون مشتق اول
با فرض اینکه نقطهٔ بحرانی تابع است و و روی پیوسته و به جز احتمالاً در مشتقپذیر باشد:
- اگر روی مثبت و روی منفی باشد، آنگاه در ماکزیمم نسبی دارد.
- اگر روی منفی و روی مثبت باشد، آنگاه در مینیمم نسبی دارد.
- اگر روی و همعلامت باشد، آنگاه در اکسترمم ندارد.
آزمون مشتق دوم
فرض کنید نقطهٔ بحرانی تابع و موجود باشد:
- اگر باشد آنگاه در دارای نسبی است.
- اگر باشد آنگاه در دارای نسبی است.
- اگر باشد آزمون بینتیجه است.
جهت تقعر و نقطهٔ عطف
اگر نمودار تابعی به صورت باشد، تقعر آن به سمت بالاست. در این حالت منحنی بالای هر خطی که بر آن مماس شود، قرار میگیرد. به عبارت دیگر اگر صعودی اکید باشد یا روی بازهٔ موجود و همواره مثبت باشد، آنگاه جهت تقعر نمودار روی این بازه رو به بالاست.
اگر نمودار تابعی به صورت باشد، تقعر آن به سمت پایین است. در این حالت منحنی پایین هر خطی که بر آن مماس شود، قرار میگیرد. به عبارت دیگر اگر نزولی اکید باشد یا روی بازهٔ موجود و همواره منفی باشد، آنگاه جهت تقعر نمودار روی این بازه رو به پایین است.
نقطهٔ عطف
اگر جهت تقعر نمودار در نقطهٔ تغییر کند و مماس نیز داشته باشد، آنگاه را نقطهٔ عطف گویند. در بررسی نقطهٔ عطف تابع، سه شرط زیر باید برقرار باشد:
- در پیوسته باشد.
- در فقط یک مماس داشته باشد. (مایل، افقی یا قائم)
- جهت تقعر در تغییر کند.
پس برای یافتن نقاط عطف نمودار تابع کافی است، نقاطی که در آنها وجود ندارد یا برابر صفر است را تعیین و علامت را قبل و بعد از این نقاط و نیز وجود خط مماس را در این نقاط بررسی کنیم.
قاعدهٔ هوپیتال
از قاعدهٔ هوپیتال برای رفع ابهام و در حد استفاده میشود بهطوریکه اگر و در مشتقپذیر باشند و آنگاه:
اگر و در از راست مشتق داشته باشد از قاعدهٔ هوپیتال برای وقتی میتوان استفاده کرد و به همین ترتیب، اگر مشتق چپ داشته باشد برای .[۲]
بهینهسازی
بسیاری از مسائلی که در علوم تجربی و ریاضیات مطرح میشوند، در جستجوی یافتن مقادیر ماکزیمم و مینیممی هستند که یک تابع مشتقپذیر میتواند در دامنهٔ خاص اختیار کند و مشتق ابزار مناسبی برای یافتن این مقادیر است.
برای حل مسائل بهینهسازی لازم است ابتدا کمیتهایی مانند حجم، مساحت، فاصله و… که بیشترین یا کمترین مقدار آن مورد نیاز است، به صورت تابعی از متغیرهای دیگر نوشته شود و چنانچه معادلهٔ حاصل بیش از یک متغیر داشت با استفاده از فرضیات مسئله و ارتباط متغیرها با هم، معادله را به معادلهای با یک متغیر مستقل تبدیل کرد و در انتها به کمک مشتق، نقاط بحرانی را یافت، تا بتوان ماکزیمم و مینیمم مطلق تابع را مشخص کرد.[۱۲]
معادلات دیفرانسیل
معادلات دیفرانسیل یک معادله ریاضی است و بیانگر یک تابع مجهول از یک یا چند متغیر مستقل و مشتقهای مرتبههای مختلف آن نسبت به متغیرهای مستقل میباشد. فرض کنید f تابعی معین از x, y و مشتقات y باشد. در این صورت معادلهای به فرم زیر:
یک معادلهٔ دیفرانسیل معمولی صریح از مرتبهٔ n نامیده میشود. در حالت کلی تر فرم ضمنی معادلهٔ دیفرانسیل معمولی از مرتبهٔ n به صورت زیر میباشد:
بهطور کل معادلات دیفرانسیل به سه روش تحلیلی، نیمه تحلیلی و عددی قابل حل میباشد.[۱۳]
قواعد مشتقگیری
در روابط زیر ، و اعداد ثابت، ،،،، متغیر و عدد نپر است.[۱۴][۱۵][۱۶]
توابع جبری
مشتق تمامی توابع جبری به شکل زیر است:
|
|
توابع مثلثاتی
تقریباً مشتق تمامی توابع مثلثاتی مشهور و پر کاربرد به شکل زیر است:
|
|
|
|
|
|
توابع معکوس مثلثاتی
|
|
|
توابع نمایی و لگاریتمی
تقریباً مشتق تمامی توابع نمایی مشهور و پر کاربرد به شکل زیر است:
|
|
|
توابع هذلولی
مشتق یکسری از توابع هذلولی به صورت زیر میباشد:
|
|
|
جستارهای وابسته
منابع
پانویس
- ↑ آدامز، کریستوفر اسکس (۲۰۰۹). حساب دیفرانسیل و انتگرال. Pearson Education Canada. شابک ۹۷۸۰۳۲۱۵۴۹۲۸۰.
- ↑ ۲٫۰ ۲٫۱ کارل بویر (۱۹۶۸). A History of Mathematics.
- ↑ فرانک آیرز، الیوت مندلسون (۱۳۸۹). حساب دیفرانسیل و انتگرال- رئوس مطالب. ترجمهٔ لیلا فرخی. سناباد. شابک ۹۷۸-۹۶۴-۶۶۸۶-۶۶-۳.
- ↑ محمد حسن بیژن زاده، وحید عالمیان، غلامعلی فرشادی (۱۳۹۳). حساب دیفرانسیل و انتگرال- دوره پیش دانشگاهی-رشته علوم ریاضی. شرکت چاپ و نشر کتابهای درسی ایران. شابک ۹۷۸-۹۶۴-۰۵-۲۰۰۹-۳.
- ↑ جورج توماس (۲۰۱۴). حساب دیفرانسیل و انتگرال توماس (ویراست دوازدهم). شابک ۹۷۸-۹۶۴-۲۰۸-۰۶۹-۴.
- ↑ Banach, S. (1931), "Uber die Baire'sche Kategorie gewisser Funktionenmengen", Studia. Math. (3): 174–179.. Cited by Hewitt, E; Stromberg, K (1963), Real and abstract analysis, Springer-Verlag, Theorem 17.8
- ↑ حساب دیفرانسیل و انتگرال (جلد اول)، دکتر مسعود نیکوکار و بهمن عرب زاده، تهران، انتشارات آزاده، ۱۳۸۲، شابک ۹۶۴−۸۰۲۰−۴۷−۷
- ↑ جورج توماس - راس فینی (۱۳۷۰). حساب دیفرانسیل و انتگرال و هندسه تحلیلی (جلد اول). ترجمهٔ سیامک کاظمی - مهدی بهزاد - علی کافی. مرکز نشر دانشگاهی. شابک ۹۶۴-۰۱-۰۵۳۶-۸.
- ↑ ریچارد سیلورمن (۱۳۷۶). حساب دیفرانسیل و انتگرال و هندسه تحلیلی جدید. ترجمهٔ علیاکبر عالمزاده. شابک ۹۶۴-۶۲۱۵-۰۶-۸.
- ↑ دکتر مسعود نیکوکار و بهمن عرب زاد (۱۳۸۴). حساب دیفرانسیل و انتگرال. ج. اول. انتشارات آزاده. شابک ۹۶۴-۸۰۲۰-۴۷-۷.
- ↑ Stewart، James (۲۰۰۸). Calculus: Early Transcendentals. Brooks/Cole. شابک ۰-۴۹۵-۰۱۱۶۶-۵.
- ↑ بردلی اس هاکس (۱۹۷۷). برنامهنویسی کاربردی ریاضیات. ادیسون وسلی.
- ↑ سیمونز. جورج اف. معادلات دیفرانسیل وکاربردآنها. ترجمهٔ علی اکبر بابایی.
- ↑ Complex Variables, M.R. Speigel, S. Lipschutz, J.J. Schiller, D. Spellman, Schaum's Outlines Series, McGraw Hill (USA), 2009, ISBN 978-0-07-161569-3
- ↑ Calculus (5th edition), F. Ayres, E. Mendelson, Schuam's Outline Series, 2009, ISBN 978-0-07-150861-2.
- ↑ Advanced Calculus (3rd edition), R. Wrede, M.R. Spiegel, Schuam's Outline Series, 2010, ISBN 978-0-07-162366-7.
کتابشناسی
- باریس پاولوویچ دمیدوویچ (۱۳۸۹)، تمرینها و مسائل آنالیز ریاضی، پرویز شهریاری، وزارت علوم و آموزش عالی، شابک ۹۷۸-۹۶۴-۰۰-۰۲۸۲-۷
- جورج توماس و راس فینی (۱۳۷۰)، حساب دیفرانسیل و انتگرال و هندسهٔ تحلیلی، مرکز نشر دانشگاهی، شابک ۹۷۸-۹۶۴-۰۱-۰۵۳۶-۸
- ریچارد سیلورمن (۱۳۷۸)، حساب دیفرانسیل و انتگرال و هندسهٔ تحلیلی، انتشارات علمی و فنی، شابک ۹۶۴-۶۲۱۵-۰۶-۸
- تام اپوستل (۱۳۷۵)، حساب دیفرانسیل و انتگرال، مرکز نشر دانشگاهی، شابک ۹۶۴-۰۱-۰۰۰۷-۲
- پرویز شهریاری (۱۳۸۳)، تاریخ ریاضیات، انتشارات مدرسه، شابک ۹۶۴-۳۸۵-۳۰۱-۲
- ویلفرد کاپلان و دونالد جی لوییس (۱۳۶۹)، حساب دیفرانسیل و انتگرال و جبر خطی، مؤسسهٔ انتشارات دانشگاه تهران
پیوند به بیرون
- ماشین مشتقگیر برای نمونه معادله در این لینک موجود است.
- حسابگر توابع WIMS محاسبهٔ برخط مشتق توابع؛ این نرمافزار، شامل تمرینهای تعاملی نیز هست.
- دستیار ریاضی روی وب محاسبهٔ برخط مشتق توابع؛ شامل توضیح مراحل محاسبه.
- تمرین مشتقگیری از توابع تصادفی



























































![{\displaystyle (c,a]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17969d8bb1d3afd713d9133af0227f32fe54524c)















































































![{\displaystyle [a,b]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6db8e01502a6bed98f89b7bb2127c620f288f605)






























































![{\displaystyle \left({\sqrt[{m}]{u}}\;\right)'={\frac {u'}{m{\sqrt[{m}]{u^{m-1}}}}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0803fd382995e56caf255727740030ea9e65ced2)




![{\displaystyle \left({\sqrt[{m}]{u^{p}}}\;\right)'={\frac {pu'}{m{\sqrt[{m}]{u^{m-p}}}}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2934f79540fa2b662dc41d20ef8b8003e1308e4a)

























