Histopathology image classification: Highlighting the gap between manual analysis and AI automation
Contents
-
(Top)
-
1 History
-
2 Parallel Implementation of Isolation Forest
-
3 Isolation trees
-
4 Anomaly detection
-
5 Properties
-
6 Parameter Selection
-
7 SCiForest
-
8 SCiForest Implementation Differences
-
9 Extended Isolation Forest
-
10 Improvements in Extended Isolation Forest
-
11 Open source implementations
-
12 Python implementation with Scikit-learn
-
13 Isolation Forest example
-
14 Diagrams for comparing path lengths for normal vs anomalous points:
-
15 Sub-sampling affects performance of isolation forest:
-
16 See also
-
17 References
Isolation Forest is an algorithm for data anomaly detection using binary trees. It was developed by Fei Tony Liu in 2008.[1] It has a linear time complexity and a low memory use, which works well for high-volume data.[2][3] It is based on the assumption that because anomalies are few and different from other data, they can be isolated using few partitions. Like decision tree algorithms, it does not perform density estimation. Unlike decision tree algorithms, it uses only path length to output an anomaly score, and does not use leaf node statistics of class distribution or target value.
Isolation Forest is fast because it splits the data space, randomly selecting an attribute and split point. The anomaly score is inversely associated with the path-length because anomalies need fewer splits to be isolated, because they are few and different.
History
The Isolation Forest (iForest) algorithm was initially proposed by Fei Tony Liu, Kai Ming Ting and Zhi-Hua Zhou in 2008.[2] In 2012 the same authors showed that iForest has linear time complexity, a small memory requirement, and is applicable to high-dimensional data.[3] In 2010, an extension of the algorithm, SCiforest, was published to address clustered and axis-paralleled anomalies.[4]
Parallel Implementation of Isolation Forest
The Isolation Forest algorithm is well-suited for parallelization because the trees in the forest are built independently. This allows for efficient scaling, particularly when working with large datasets. Below are the key aspects of how parallel implementation is achieved:
Parallel Tree Construction:
Independent Trees: Each tree in the Isolation Forest is built independently, making it possible to construct multiple trees in parallel.
Task Distribution: The process of building trees can be divided across multiple processors or computing nodes. For example, if there are t trees and n processors, each processor can handle t/n trees.
Concurrency: Parallel computing tools like Apache Spark, Hadoop, or Python libraries such as joblib or multiprocessing can manage the concurrent construction of trees.
Data Partitioning:
Random Sampling: Each tree is built using a random sample from the dataset. This sampling can be parallelized, with each processor working on a different subset of data.
Data Distribution: In a distributed system, the dataset can be divided into smaller chunks and assigned to different nodes, which will each independently build their portion of the trees.
Parallel Anomaly Scoring:
Independent Scoring: Scoring the data points for anomalies can also be parallelized. Each data point is processed by each tree independently.
Task Distribution: Scoring tasks can be distributed across processors or nodes, allowing for efficient handling of large datasets.
Aggregating Results:
Combining Scores: After scoring, the anomaly scores from all trees need to be combined for each data point. This involves gathering the scores and calculating the final anomaly score.
Efficient Aggregation: The aggregation process can be parallelized using reduction operations in parallel computing frameworks, which speeds up the process.
Implementation Frameworks:
Apache Spark: Spark’s distributed data processing capabilities (using RDDs or DataFrames) make it a good choice for implementing a parallel Isolation Forest.
Hadoop MapReduce: While not typically used for machine learning, Hadoop’s MapReduce framework can be adapted for parallel tree construction and anomaly scoring.
Python Libraries: Python tools like joblib, multiprocessing, and Dask make it easy to implement parallelism, whether on a single machine or across multiple nodes in a cluster.
Isolation trees
The premise of the Isolation Forest algorithm is that anomalous data points are easier to separate from the rest of the sample. In order to isolate a data point, the algorithm recursively generates partitions on the sample by randomly selecting an attribute and then randomly selecting a split value between the minimum and maximum values allowed for that attribute.
An example of random partitioning in a 2D dataset of normally distributed points is shown in the first figure for a non-anomalous point and in the second one for a point that is more likely to be an anomaly. It is apparent from the pictures how anomalies require fewer random partitions to be isolated, compared to normal points.
Recursive partitioning can be represented by a tree structure named Isolation Tree, while the number of partitions required to isolate a point can be interpreted as the length of the path, within the tree, to reach a terminating node starting from the root. For example, the path length of point in the first figure is greater than the path length of in the second figure.
Let be a set of d-dimensional points and . An Isolation Tree (iTree) is defined as a data structure with the following properties:
- for each node in the Tree, is either an external-node with no child, or an internal-node with one “test” and exactly two child nodes ( and )
- a test at node consists of an attribute and a split value such that the test determines the traversal of a data point to either or .
In order to build an iTree, the algorithm recursively divides by randomly selecting an attribute and a split value , until either
- the node has only one instance, or
- all data at the node have the same values.
When the iTree is fully grown, each point in is isolated at one of the external nodes. Intuitively, the anomalous points are those (easier to isolate, hence) with the smaller path length in the tree, where the path length of point is defined as the number of edges traverses from the root node to get to an external node.
A probabilistic explanation of iTree is provided in the original iForest paper.[2]
Anomaly detection
Anomaly detection with Isolation Forest is done as follows:[4]
- Use the training dataset to build some number of iTrees
- For each data point in the test set:
- Pass it through all the iTrees, counting the path length for each tree
- Assign an “anomaly score” to the instance
- Label the point as “anomaly” if its score is greater than a predefined threshold, which depends on the domain
Anomaly score
The algorithm for computing the anomaly score of a data point is based on the observation that the structure of iTrees is equivalent to that of Binary Search Trees (BST): a termination to an external node of the iTree corresponds to an unsuccessful search in the BST.[4] Therefore the estimation of average for external node terminations is the same as that of the unsuccessful searches in BST, that is[5]
where is the test set size, is the sample set size and is the harmonic number, which can be estimated by , where is the Euler-Mascheroni constant.
Above, is the average given , so we can use it to normalize to get an estimate of the anomaly score for a given instance x:
where is the average value of from a collection of iTrees. For any data point :
- if is close to then is very likely an anomaly
- if is smaller than then is likely normal
- if all points in the sample score around , then likely they are all normal
Properties
- Sub-sampling: Because iForest does not need to isolate normal instances, it can often ignore most of the training set. Thus, it works very well when the sampling size is kept small, unlike most other methods, which benefit from a large sample size.[2][3]
- Swamping: When normal instances are too close to anomalies, the number of partitions required to separate anomalies increases, a phenomenon known as swamping, which makes it more difficult for iForest to discriminate between anomalies and normal points. A main reason for swamping is the presence of too much data; so a possible solution is sub-sampling. Because iForest performs well under sub-sampling, reducing the number of points in the sample is also a good way to reduce the effect of swamping.[2]
- Masking: When there are many anomalies, some of them can aggregate in a dense, large cluster, making it more difficult to separate the single anomalies and so to identify them. This phenomenon is called “masking”, and as with swamping, is more likely when the sample is big and can be alleviated through sub-sampling.[2]
- High-dimensional data: A main limitation of standard, distance-based methods is their inefficiency in dealing with high dimensional data.[6] The main reason is that in a high-dimensional space, every point is equally sparse, so using a distance-based measure of separation is ineffective. Unfortunately, high-dimensional data also affects the detection performance of iForest, but the performance can be vastly improved by using feature selection, like Kurtosis, to reduce the dimensionality of the sample.[2][4]
- Normal instances only: iForest performs well even if the training set contains no anomalous points.[4] This is because iForest describes data distributions such that long tree paths correspond to normal data points. Thus, the presence of anomalies is irrelevant to detection performance.
Parameter Selection
Selecting appropriate parameters is the key to the performance of the Isolation Forest algorithm. Each of the parameters influences anomaly detection differently.
Key parameters include:
- Number of Trees : The number of trees in the ensemble. More trees make it better at finding unusual patterns but also raise the cost of computing. Commonly used range is 100 to 300 which balances accuracy with how efficiently it uses computing power.[2]
- Subsample Size : The size of the sample that is used to construct each tree. Smaller sample sizes reduce computational complexity, while larger sample sizes capture more data variability. A common value for subsample size is 256, though the optimal value can vary depending on the dataset's characteristics.[2]
- Contamination Factor : An estimate of the proportion of outliers in the dataset. The higher the contamination factor, the more points are flagged as anomalies, and the lower it is, the fewer points it marks. It is usually determined by knowledge of the field or cross-validation. Finding the right value for contamination is important to avoid false positives and false negatives.[3]
- Tree Depth : This refers to the number of features that can be considered for a split in each tree. The smaller the tree depth, the faster the training is; however, it can make it difficult for the model to find anomalies, especially in complex datasets. Finding the right balance between depth and training speed is crucial. For example, shallow trees may perform well for simple datasets but struggle with high-dimensional or noisy data.[3]
- Split Selection Strategy : Splits are selected randomly between the minimum and maximum values of each feature in the sample, while maintaining efficiency and reducing overfitting. In the case of more complex data, other methods can be used.[4]
- Random Seed : Setting a fixed random seed ensures that the results from the algorithm will be reproducible over multiple runs. This is very important when comparing models or tuning hyperparameters because it avoids differences due to randomness. The stability of the results in each stage of running many iterations or cross-validation is essential.[7] [8]
The table below shows the summary of parameter selection based on dataset characteristics:
| Parameter | Small Datasets | Large Datasets | High-Dimensional Data | Imbalanced Datasets |
|---|---|---|---|---|
| Number of Trees | 50–100 | 200+ | Higher values for better accuracy | Increase if many anomalies are expected |
| Subsample Size | 100+ | 512+ | Reduce to avoid overfitting | Larger subsample size for better accuracy |
| Contamination Factor | Set based on domain knowledge | Set based on domain knowledge | Default (None) | Increase for many anomalies |
| Tree Depth | Shallow (1–2) | Deeper (max features) | Limit to prevent overfitting | Set lower for generalization |
| Split Selection Strategy | Random splits | Random splits | Random splits (default) | Default, unless anomalies are complex |
| Random Seed | Set for reproducibility | Set for reproducibility | Set for reproducibility | Set for consistency |
SCiForest
SCiForest (Isolation Forest with Split-selection Criterion) is an extension of the original Isolation Forest algorithm. It targets specifically clustered anomalies through selecting a split criterion and finding hyper-planes that are more likely to produce good results. SCiForest introduces random hyper-planes which are non-axis-parallel to the original attributes. Since it is not necessary to have the optimal hyper-plane in every node, with sufficient trials of randomly generated hyper-planes a good enough hyper-plane will emerge. Therefore, the resulting model is considerably effective due to aggregate power of the ensemble learner[4].
SCiForest Implementation Differences
SciForest introduces several key differences from traditional Isolation Forest, particularly in its ability to handle streaming data, adapt to evolving patterns, and optimize memory and computational efficiency.
Streaming Capability:
SCiForest is specifically engineered for streaming data, enabling real-time anomaly detection. It processes data in a single pass, making it well-suited for continuous, incoming data streams. In contrast, traditional Isolation Forest typically operates in batch mode, requiring the entire dataset to be available for processing, which can be inefficient for real-time applications.
Contextual Information:
SCiForest enhances anomaly detection by incorporating contextual information, such as additional features or metadata, into the analysis. This allows the algorithm to consider the broader context of the data, improving detection accuracy. Traditional Isolation Forest focuses primarily on the features of the data itself without explicitly including external contextual information.
Adaptability:
Unlike the traditional Isolation Forest, which is generally static once trained, SCiForest is capable of adapting to changes in data distribution over time. It updates its model incrementally as new data arrives, making it more resilient to evolving data patterns and dynamic environments.
Memory Efficiency:
SCiForest is designed with memory efficiency in mind, which is essential for handling large-scale streaming data. By maintaining a compact representation of the data, it reduces memory usage. Traditional Isolation Forest may require significant memory resources to store the entire dataset and forest of trees, which can be a limitation when dealing with large datasets.
Computational Efficiency:
SCiForest minimizes computational load by updating its model incrementally, enabling efficient real-time processing. In contrast, traditional Isolation Forest is computationally demanding, as it requires building and traversing multiple trees, especially for large datasets.
Anomaly Scoring:
SCiForest employs a dynamic anomaly scoring mechanism that adjusts as new data is processed and contextual information is integrated. Traditional Isolation Forest uses a static scoring method based on isolation paths within the feature space, which may not be as responsive to changing data.
Use Cases:
SCiForest is particularly suited for applications that require real-time anomaly detection, such as fraud detection, network security monitoring, and predictive maintenance. On the other hand, traditional Isolation Forest is more appropriate for offline anomaly detection tasks involving static datasets, such as historical data analysis[9]
Extended Isolation Forest
Extended Isolation Forest (Extended IF or EIF) is another extension of the original Isolation Forest algorithm. Extended IF uses rotated trees in different planes, similarly to SCiForest and random values are selected to split the data, such as a random slope or intercept.
The standard Isolation Forest requires two pieces of information, those being 1) a random feature or coordinate, and 2) a random value for the feature from the range of available values in the data. The Extended IF also requires only two pieces of information, this time being 1) a random feature or coordinate, and 2) a random value for the feature from the range of available values in the data. This makes the Extended IF simpler than using rotation trees[10].

The figure depicts a score map of a regular Isolation Forest in comparison to an Extended Isolation Forest for a sinusoidal-shaped data-set. This image allows us to clearly observe the improvement made by the Extended Isolation Forest in evaluating the scores much more accurately when compared to the shape of the data. The original EIF publication includes also this comparison with a single-blob-shaped data-set and a two-blob-shaped data-set, also comparing the EIF results to isolation forest using rotation trees[10].
Improvements in Extended Isolation Forest
The Extended Isolation Forest enhances the traditional Isolation Forest algorithm by addressing some of its limitations, particularly in handling high-dimensional data and improving anomaly detection accuracy. Key improvements in EIF include:
Enhanced Splitting Mechanism: Unlike traditional Isolation Forest, which uses random axis-aligned splits, EIF uses hyperplanes for splitting data. This approach allows for more flexible and accurate partitioning of the data space, which is especially useful in high-dimensional datasets.
Improved Anomaly Scoring: EIF refines the anomaly scoring process by considering the distance of data points from the hyperplane used in splitting. This provides a more granular and precise anomaly score, leading to better differentiation between normal and anomalous points.
Handling of High-Dimensional Data: The use of hyperplanes also improves EIF’s performance in high-dimensional spaces. Traditional Isolation Forest can suffer from the curse of dimensionality in such scenarios, but EIF mitigates this issue by creating more meaningful and informative partitions in the data space.[11]
Open source implementations
Original implementation by Fei Tony Liu is Isolation Forest in R.
Other implementations (in alphabetical order):
- ELKI contains a Java implementation.
- Isolation Forest - A distributed Spark/Scala implementation with Open Neural Network Exchange (ONNX) export for easy cross-platform inference.[12]
- Isolation Forest by H2O-3 - A Python implementation.
- Package solitude implementation in R.
- Python implementation with examples in scikit-learn.
- Spark iForest - A distributed Apache Spark implementation in Scala/Python.
- PyOD IForest - Another Python implementation in the popular Python Outlier Detection (PyOD) library.
Other variations of Isolation Forest algorithm implementations:
- Extended Isolation Forest – An implementation of Extended Isolation Forest. [10]
- Extended Isolation Forest by H2O-3 - An implementation of Extended Isolation Forest.
- (Python, R, C/C++) Isolation Forest and variations - An implementation of Isolation Forest and its variations.[13]
Python implementation with Scikit-learn
The isolation forest algorithm is commonly used by data scientists through the version made available in the scikit-learn library. The snippet below depicts a brief implementation of an isolation forest:
import pandas as pd
from sklearn.ensemble import IsolationForest
# Consider 'data.csv' is a file containing samples as rows and features as column, and a column labeled 'Class' with a binary classification of your samples.
df = pd.read_csv('data.csv')
X = df.drop(columns=['Class'])
y = df['Class']
# Determine how many samples will be outliers based on the classification
outlier_fraction = len(df[df['Class']==1])/float(len(df[df['Class']==0]))
# Create and fit model, parameters can be optimized
model = IsolationForest(n_estimators=100, contamination=outlier_fraction, random_state=42)
model.fit(df)
This snippet is a shortened adapted version of an implementation explored by GeeksforGeeks, which can be accessed for further explorations[14].
Isolation Forest example
An example using isolation forest for anomaly detection will be visualize the decision boundary of an Isolation Forest trained on a toy dataset.
- [15]
-
1.1) It is example of generating 2 clusters and each one containing no.of samples=n and sampling randomly the standard normal distribution using the function called
numpy.random.randn[16]. The two of the Clusters (Gaussian inliers ) are assigned with ground truth label 1 and outliers created usingnumpy.random.uniform[17] is assigned with label -1.
Plotting discrete decision boundary:
-
[1] 1.2) The color in the background represents that the sample present in that area is outlier or not a outlier. And the scatter plot represents the true labels.
Plotting path length decision boundary:
-
[2]1.3)response_method="decision_function"[18] here by setting response method to decision function , the
DecisionBoundaryDisplay[19] displays the value of normality of an observation. The path length averaged over a forest of random trees, which is in turn determined depth of the leaf (or same the no.of splits) necessary to isolate a particular sample, provides this score. when forest of random tree produces shortest path lengths for isolating particular samples, those are most likely to be anomalies and the normality value is close to 0 and large path the value close to 1 are inliers.
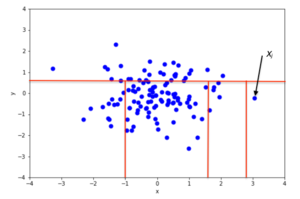
Diagrams for comparing path lengths for normal vs anomalous points:
-
1.4)anomaly point A is isolated by just one split on x1.[20]
-
1.5)Anomaly point A has less average length compared to Normal Point.[21]
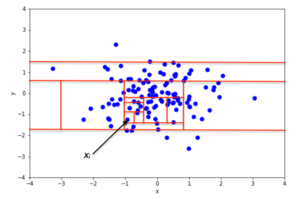
Sub-sampling affects performance of isolation forest:
-
1.6)As the image of sub-sampling shows two clusters one is standalone cluster and other one is mix of normal and anamalous points by removing the clutter. And the no.of samples increases each individual tree becomes a tuning parameter in addition to no.of trees are mentioned.[22]
See also
References
- ^ Liu, Fei Tony. "First Isolation Forest implementation on Sourceforge".
- ^ a b c d e f g h i Liu, Fei Tony; Ting, Kai Ming; Zhou, Zhi-Hua (December 2008). "Isolation Forest". 2008 Eighth IEEE International Conference on Data Mining. pp. 413–422. doi:10.1109/ICDM.2008.17. ISBN 978-0-7695-3502-9. S2CID 6505449.
- ^ a b c d e Liu, Fei Tony; Ting, Kai Ming; Zhou, Zhi-Hua (December 2008). "Isolation-Based Anomaly Detection". ACM Transactions on Knowledge Discovery from Data. 6: 3:1–3:39. doi:10.1145/2133360.2133363. S2CID 207193045.
- ^ a b c d e f g Liu, Fei Tony; Ting, Kai Ming; Zhou, Zhi-Hua (September 2010). "On Detecting Clustered Anomalies Using SCiForest". Joint European Conference on Machine Learning and Knowledge Discovery in Databases - ECML PKDD 2010: Machine Learning and Knowledge Discovery in Databases. Lecture Notes in Computer Science. Vol. 6322. pp. 274–290. doi:10.1007/978-3-642-15883-4_18. ISBN 978-3-642-15882-7.
- ^ Shaffer, Clifford A. (2011). Data structures & algorithm analysis in Java (3rd Dover ed.). Mineola, NY: Dover Publications. ISBN 9780486485812. OCLC 721884651.
- ^ Dilini Talagala, Priyanga; Hyndman, Rob J.; Smith-Miles, Kate (12 Aug 2019). "Anomaly Detection in High Dimensional Data". arXiv:1908.04000 [stat.ML].
- ^ "numpy.random.randn — NumPy v2.1 Manual". numpy.org. Retrieved 2024-11-21.
- ^ "numpy.random.uniform — NumPy v2.1 Manual". numpy.org. Retrieved 2024-11-21.
- ^ Heigl, Michael; Anand, Kumar Ashutosh; Urmann, Andreas; Fiala, Dalibor; Schramm, Martin; Hable, Robert (2021-06-24). "On the Improvement of the Isolation Forest Algorithm for Outlier Detection with Streaming Data". Electronics. 10 (13): 1534. doi:10.3390/electronics10131534. ISSN 2079-9292.
- ^ a b c d Hariri, Sahand; Kind, Matias Carrasco; Brunner, Robert J. (April 2021). "Extended Isolation Forest". IEEE Transactions on Knowledge and Data Engineering. 33 (4): 1479–1489. arXiv:1811.02141. doi:10.1109/TKDE.2019.2947676. ISSN 1558-2191. S2CID 53236735.
- ^ Hariri, Sahand; Kind, Matias Carrasco; Brunner, Robert J. (2021-04-01). "Extended Isolation Forest". IEEE Transactions on Knowledge and Data Engineering. 33 (4): 1479–1489. doi:10.1109/TKDE.2019.2947676. ISSN 1041-4347.
- ^ Verbus, James (13 August 2019). "Detecting and preventing abuse on LinkedIn using isolation forests". LinkedIn Engineering Blog. Retrieved 2023-07-02.
- ^ Cortes, David (2019). "Distance approximation using Isolation Forests". arXiv:1910.12362 [stat.ML].
- ^ GeeksforGeeks, What is Isolation Forest?, accessed November 19th, 2024.
- ^ "Gaussian Clusters vs Uniform distributed outliers".
- ^ "numpy.random.randn — NumPy v2.1 Manual". numpy.org. Retrieved 2024-11-21.
- ^ "numpy.random.uniform — NumPy v2.1 Manual". numpy.org. Retrieved 2024-11-21.
- ^ scikitlearn.org (Jul 11, 2019). "IsolationForest example".
- ^ "DecisionBoundaryDisplay".
- ^ "Plotting of anomaly point". 11 July 2019.
- ^ "Shorter average length for anomaly point". 11 July 2019.
- ^ "sub-sampling affects isolation forest". 11 July 2019.












































![1.1) It is example of generating 2 clusters and each one containing no.of samples=n and sampling randomly the standard normal distribution using the function called numpy.random.randn[16]. The two of the Clusters (Gaussian inliers ) are assigned with ground truth label 1 and outliers created using numpy.random.uniform[17] is assigned with label -1.](https://upload.wikimedia.org/wikipedia/commons/c/c9/Gaussian_inliers_vs_Distributed_outliers.png)
![[1] 1.2) The color in the background represents that the sample present in that area is outlier or not a outlier. And the scatter plot represents the true labels.](https://upload.wikimedia.org/wikipedia/commons/thumb/9/98/Discrete_decision_boundary.png/500px-Discrete_decision_boundary.png)
![[2]1.3)response_method="decision_function"[18] here by setting response method to decision function , the DecisionBoundaryDisplay[19] displays the value of normality of an observation. The path length averaged over a forest of random trees, which is in turn determined depth of the leaf (or same the no.of splits) necessary to isolate a particular sample, provides this score. when forest of random tree produces shortest path lengths for isolating particular samples, those are most likely to be anomalies and the normality value is close to 0 and large path the value close to 1 are inliers.](https://upload.wikimedia.org/wikipedia/commons/thumb/0/07/Path_length_decision_boundary.png/500px-Path_length_decision_boundary.png)
![1.4)anomaly point A is isolated by just one split on x1.[20]](https://upload.wikimedia.org/wikipedia/commons/thumb/2/23/Anomaly_Point.png/400px-Anomaly_Point.png)
![1.5)Anomaly point A has less average length compared to Normal Point.[21]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/14/Comparsion_of_Normal_vs_anomalous_points.png/400px-Comparsion_of_Normal_vs_anomalous_points.png)
![1.6)As the image of sub-sampling shows two clusters one is standalone cluster and other one is mix of normal and anamalous points by removing the clutter. And the no.of samples increases each individual tree becomes a tuning parameter in addition to no.of trees are mentioned.[22]](https://upload.wikimedia.org/wikipedia/commons/thumb/b/b7/Sub-sampling_affects_performance_of_isolation_forest.png/400px-Sub-sampling_affects_performance_of_isolation_forest.png)

