FAIR and interactive data graphics from a scientific knowledge graph

Den analytiska geometrin är en gren av geometrin där algebraiska metoder från främst linjär algebra används för att lösa geometriska problem. Att de reella talens algebra kan användas för lösning av geometriska problem vilar på Cantor-Dedekinds axiom.

Metoder från analytisk geometri används inom alla tillämpade vetenskaper, men särskilt inom fysiken, till exempel för beskrivningen av planeternas banor. Ursprungligen behandlade analytisk geometri endast frågor rörande planet och den rumsliga (euklidiska) geometrin. Mera allmänt beskriver den analytiska geometrin affina rum av godtyckliga dimensioner över godtyckliga kroppar.

Koordinatsystem

Grundläggande för analytisk geometri är begagnandet av ett koordinatsystem. Vanligen används ett kartesiskt koordinatsystem ^[1].

Analytisk geometri i R²

Koordinatsystem och transformationer

Med (x, y) betecknas de ursprungliga koordinaterna och med (x', y') de nya.

Parallellförskjutning

Om x₀, y₀ är koordinaterna för origo i det nya systemet, så gäller:

x'=x-x_{0},\quad y'=y-y_{0}\,

Rotation

Om rotationsvinkeln $\alpha$ räknas positiv (den vinkel som positiva x-axeln behöver vridas för att sammanfalla med positiva y-axeln) blir transformationsformlerna

x'=x\cos \alpha +y\sin \alpha \quad x=x'\cos \alpha -y'\sin \alpha \,

y'=y\cos \alpha -x\sin \alpha \quad y=x'\sin \alpha +y'\cos \alpha \,

Avståndet mellan två punkter

Avståndet mellan punkterna (x₁, y₁) och (x₂, y₂) är

{\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\,

Arean av en triangel

Om triangelns hörn har koordinaterna (x₁, y₁), (x₂, y₂) och (x₃, y₃), är dess area

\pm T={\frac {1}{2}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}=

={\frac {1}{2}}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]\,

För att T skall vara positiv, måste punkterna (x₁,y₁), (x₂, y₂) och (x₃, y₃) följa på varandra i positiv led, det vill säga moturs.

Delning av en sträcka

Delas sträckan mellan punkterna (x₁, y₁) och (x₂, y₂), i förhållandet m/n blir delningspunktens koordinater

x={\frac {mx_{2}+nx_{1}}{m+n}},\quad y={\frac {my_{2}+ny_{1}}{m+n}}\,

Vinkelkoefficienten för en rät linje

Låt $\alpha$ vara den vinkel en linje bildar med x-axeln. Om linjen går genom punkterna (x₁, y₁) och (x₂,y₂) blir vinkelkoefficienten

\tan \alpha ={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}};\quad x_{1}\neq x_{2}\,

Räta linjens ekvation

Räta linjens ekvation är en förstgradsekvation i x och y och den allmänna formen är

Ax+By+C=0\,

Varje ekvation av första graden representerar en linje.

x=a\,

betyder en rät linje parallell med y-axeln och

y=b\,

är en linje parallell med x-axeln.

y=k\,x\,

är en linje genom origo.

k-formen

Räta linjen kan skrivas på formen

y=k\,x+m\,

om linjen ej är parallell med y-axeln, det vill säga B är nollskild. Här är k linjens vinkelkoefficient

k=-{\frac {A}{B}},\quad m=-{\frac {C}{B}}\,

och m y-koordinaten för linjens skärning med y-axeln.

Interceptformen

Interceptformens parametrar är linjens skärningspunkter med x-axeln respektive y-axeln och skrivs

{\frac {x}{a}}+{\frac {y}{b}}=1

där a är x-koordinaten för linjens skärningspunkt med x-axeln och b är y-koordinaten för linjens skärningspunkt med y-axeln eller

a=-{\frac {C}{A}},\quad b=-{\frac {C}{B}}\,

Normalformen

x\cos \alpha +y\sin \alpha -m=0\,

är normalformen för den räta linjen. $\alpha$ och m bestäms ur

m=-{\frac {C}{\sqrt {A^{2}+B^{2}}}},

\cos \alpha ={\frac {A}{\sqrt {A^{2}+B^{2}}}},\quad \sin \alpha ={\frac {B}{\sqrt {A^{2}+B^{2}}}}

Kvadratrotens tecken väljs så att m blir positivt.

m är längden av normalen från origo till linjen och $\alpha$ är denna normals vinkel med x-axeln.

Avståndet från en punkt till en rät linje

Räta linjen skrivs på normalformen

x\cos \alpha +y\sin \alpha -m=0\,

Då är avståndet från punkten P med koordinaterna (x₁,y₁):

p=\pm (x_{1}\cos \alpha +y_{1}\sin \alpha -m)\,

där tecknet + väljs om origo och P ligger på olika sidor om linjen.

Enpunktsformen

Ekvationen för en rät linje genom punkten (x₁, y₁) med vinkelkoefficienten k är

y-y_{1}=k(x-x_{1})\,

Tvåpunktsformen

Ekvationen för en rät linje genom punkterna (x₁, y₁) och (x₂, y₂) är

y-y_{1}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}(x-x_{1})\,

Vinkeln mellan två linjer

Om linjernas vinkelkoefficienter är k₁ respektive k₂ bestäms vinkeln mellan linjerna av

\tan \beta ={\frac {k_{2}-k_{1}}{1+k_{1}k_{2}}}\,

Plana kurvor

En kurva i ett ortogonalt koordinatsystem ger ett funktionssamband mellan koordinaterna x och y.

Kurvans ekvation kan vara i explicit form

y=f(x)\,

i implicit form

F(x,y)=0\,

eller i parameterform

x=x(t),\quad y=y(t)\,

I polära koordinater $(r,\psi )$ blir kurvans ekvation

r=f(\psi )\,

eller

F(r,\psi )=0\,

Tangenten

Vinkelkoefficienten för tangenten till en kurva i rätvinkliga koordinater är lika med funktionens derivata i tangeringspunkten:

k={\frac {dy}{dx}}={\frac {d\,f(x)}{dx}}\,

k=-{\frac {\frac {\partial F}{\partial x}}{\frac {\partial F}{\partial y}}}\,\quad {\text{(implicit form)}}

k={\frac {y'(t)}{x'(t)}}\,\quad {\text{(parameterform)}}

Asymptoter

Med en asymptot till en kurva menas en linje sådan att avståndet mellan linjen och en punkt på kurvan går mot noll då punkten går mot oändligheten.

Om en asymptot till kurvan y = f(x) har ekvationen y = kx + m, bestäms k och m enligt

k=\lim _{x\rightarrow \infty }{\frac {f(x)}{x}},\quad m=\lim _{x\rightarrow \infty }[f(x)-kx]\,

Analytisk geometri i R³

Koordinatsystem

Som koordinatsystem i R³ används tre plan, vanligtvis vinkelräta mot varandra. Planens skärningspunkter kallas x-, y- och z-axlarna. De tre planen betecknas efter ingående axlar som xy-planet, yz-planet och xz-planet ^[2].

Rätvinkliga koordinater

Riktningscosiner

Huvudartikel: Riktningscosiner

En punkt P:s koordinater (x, y, z) är de vinkelräta avstånden till yz-, xz- och xy-planen. Om $\alpha ,\,\beta ,\,\gamma \,$ är vinklarna mellan ortsvektorn med längden r och axlarna är

x=r\cos \alpha ,\quad y=r\cos \beta ,\quad z=r\cos \gamma

där

\cos \alpha ,\,\cos \beta ,\,\cos \gamma

är riktningscosinerna vilka betecknas a, b och c och för vilka gäller

a^{2}+b^{2}+c^{2}=1\,

Vinkeln mellan två riktningar

Om två riktningar är givna, OA₁ med riktningscosinerna a₁, b₁ och c₁ och OA₂ med riktningscosinerna a₂, b₂ och c₂, så gäller för vinkeln $\theta$ mellan OA₁ och OA₂:

\cos \theta =a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}\,

Rotation av koordinatsystem

Vid övergång från ett rätvinkligt koordinatsystem (xyz) till ett annat (x'y'z') med gemensamt origo men olika axelriktningar och med riktningscosinerna i xyz-planet betecknade

för x'-axeln med

(a',b',c')\,

för y'-axeln med

(a'',b'',c'')\,

för z'-axeln med

(a''',b''',c''')\,

blir transformationformlerna

{\begin{aligned}x&=a'x'+b'y'+c'z'\\y&=a''z'+b''y'+c''z'\\z&=a'''x'+b'''y'+c'''z'\end{aligned}}{\begin{aligned}\qquad x'&=a'x+a''y+a'''z\\y'&=b'x+b''y+b'''z\\z'&=c'x+c''y+c'''z\end{aligned}}

Avståndet mellan två punkter

Avståndet d mellan punkterna (x₁, y₁, z₁) och (x₂, y₂, z₂) är

d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}\,

Om a, b och c är riktningscosinerna för en linje genom de båda punkterna, beräknas dessa som

a={\frac {x_{2}-x_{1}}{d}},\quad b={\frac {y_{2}-y_{1}}{d}},\quad c={\frac {z_{2}-z_{1}}{d}},\,

Plan i R³

Om (x₀, y₀, z₀) är en ortsvektor till en punkt i planet och (A, B, C) en normalvektor till planet, kan planets ekvation skrivas som skalärprodukten av normalvektorn och vektorn (x - x₀, y - y₀, z - z₀):

(A,B,C)(x-x_{0},y-y_{0},z-z_{0})=0\,

vilket ger den allmänna formen av planets ekvation som

Ax+By+Cz+D=0\,

där D är

-(Ax_{0}+By_{0}+Cz_{0})\,

En ekvation av första graden representerar alltid ett plan. Riktningscosinerna för planets normal är

{\frac {A}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}},\quad {\frac {B}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}},\quad {\frac {C}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}},\,

Tecknet framför roten väljs så att

{\frac {D}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}}\,

alltid är positiv. Därigenom är normalen riktad mot planets "positiva" sida.

Normalform

Genom division med

\pm {\sqrt {A^{2}+B^{2}+C^{2})}}\,

erhålls planets ekvation på normalform

x\cos \alpha +y\cos \beta +z\cos \gamma =p\,

där $\alpha ,\beta ,\gamma$ är de vinklar som planets normal bildar med koordinataxlarna och p är längden av normalen från origo till planet.

Vektorform

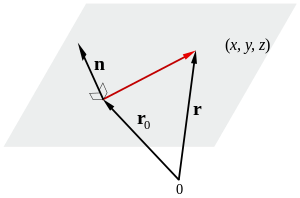
Ekvationen för ett plan med normalvektorn n, en given punkt r₀ och med r som ortsvektor för en godtycklig punkt (x, y, z) i planet är

(\mathbf {r} -\mathbf {r} _{0})\mathbf {n} =0\,

Avståndet från en punkt till ett plan

Punktens koordinater sätts in i planets normalform

x\cos \alpha +y\cos \beta +z\cos \gamma -p=0\,

och avståndet är då lika med vänsterledet med tecknet '-' om punkt och origo ligger på samma sida om planet, annars med tecknet '+'.

Exempel:

Beräkna avståndet från punkten (1, -3, 2) till planet

x+2y-2z+6=0\,

Planets ekvation i normalform

{\frac {x+2y-2z+6}{-3}}=0;\quad d={\frac {1-3\cdot 2-2\cdot 2+6}{-3}}=1\,

Vinkeln mellan två plan

Vinkeln $\omega$ mellan planen

A_{1}x+B_{1}y+C_{1}z+D_{1}=0\,

A_{2}x+B_{2}y+C_{2}z+D_{2}=0\,

bestäms av ekvationen

\cos \omega ={\frac {A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}}{{\sqrt {A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}}{\sqrt {A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}}}\,

Om planens normalvektorer är kända kan skalärprodukten av normalvektorerna användas för att bestämma vinkeln mellan planen:

\cos \omega ={\frac {\mathbf {n} _{1}\mathbf {n} _{2}}{|\mathbf {n} _{1}||\mathbf {n} _{2}|}}\,

Räta linjen

Räta linjen kan betraktas som skärningen mellan två plan och representeras av förstagradsekvationerna

A_{1}x+B_{1}y+C_{1}z+D_{1}=0\,

A_{2}x+B_{2}y+C_{2}z+D_{2}=0\,

En linje är bestämd av en punkt P = (x₀, y₀, z₀) på linjen och en riktningsvektor u:

I parameterform gäller för en punkt (x, y, z) på linjen:

(x,y,z)=(x_{0},y_{0},z_{0})+\lambda (a,b,c)\,

eller

x=x_{0}+a\lambda \,

y=y_{0}+b\lambda \,

z=z_{0}+c\lambda \,

där a, b och c är riktningskoefficienter, eller efter eliminering av parametern

{\frac {x-x_{0}}{a}}={\frac {y-y_{0}}{b}}={\frac {z-z_{0}}{c}}\,

I vektorform kan linjens ekvation skrivas

\mathbf {r} =\mathbf {r} _{0}+t\mathbf {u} \,

Kurvor i R³

En kurva i R³ kan framställas på flera sätt:

Som skärningen mellan två ytor:

F_{1}(x,y,z)=0\quad F_{2}(x,y,z)=0\,

I parameterform:

x=x(t)\quad y=y(t)\quad z=z(t)\,

I vektorform:

\mathbf {r} =x(t)\mathbf {i} +y(t)\mathbf {j} +z(t)\mathbf {k} \,

Exempel:

Skruvlinjen kan framställas i parameterform som

x=r\cos(t)\quad y=r\sin(t)\quad z=kt\,

Båglängd

Längden av ett bågelement på kurvan är

ds={\sqrt {dx^{2}+dy^{2}+dz^{2}}}\,

Längden av kurvbågen mellan t₀ och t är

s=\int _{t_{0}}^{t}{\sqrt {x'(t)^{2}+y'(t)^{2}+z'(t)^{2}}}dt\,

Tangent

Tangentens ekvation i vektorform är

\mathbf {t} =\left({\frac {d\mathbf {r} }{ds}}\right)_{0},\quad \mathbf {r} =\mathbf {r_{0}} +\lambda \left({\frac {d\mathbf {r} }{ds}}\right)_{0}\,

Normalplanet

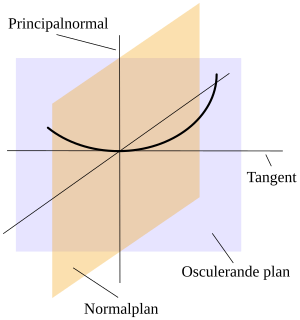
Ekvationen i vektorform för normalplanet i punkten s är

(\mathbf {r} -\mathbf {r_{0}} )\left({\frac {d\mathbf {r} }{ds}}\right)_{0}=0\,

Oskulerande planet

I en punkt på en kurva i R³ kan i allmänhet läggas oändligt många tangentplan till kurvan. Det tangentplan som närmast ansluter till kurvan kallas oskulerande planet och har ekvationen

A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0\,

där A, B och C bestäms ur formlerna

A=y'(s)z''(s)-z'(s)y''(s)\,

B=z'(s)x''(s)-x'(s)z''(s)\,

C=x'(s)y''(s)-y'(s)x''(s)\,

eller i vektorform

(\mathbf {r} -\mathbf {r} _{0})\left({\frac {d\mathbf {r} }{ds}}\times {\frac {d^{2}\mathbf {r} }{ds^{2}}}\right)_{0}=0\,

Principalnormal

Den normal till kurvan som ligger i det oskulerande planet kallas principalnormal. Dess riktning är den samma som för vektorn

\left({\frac {d^{2}\mathbf {r} }{ds^{2}}}\right)_{0}\,

Längden av denna vektor benämns krökning K, varför vektorn också kallas krökningsvektor:

K=\left|{\frac {d^{2}\mathbf {r} }{ds^{2}}}\right|_{0}={\sqrt {\left({\frac {d^{2}x}{ds^{2}}}\right)_{0}^{2}+\left({\frac {d^{2}y}{ds^{2}}}\right)_{0}^{2}+\left({\frac {d^{2}z}{ds^{2}}}\right)_{0}^{2}}}\,

Krökningsradie

Krökningsradien är krökningens inverterade värde:

R={\frac {1}{K}}={\frac {1}{\sqrt {\left({\frac {d^{2}x}{ds^{2}}}\right)_{0}^{2}+\left({\frac {d^{2}y}{ds^{2}}}\right)_{0}^{2}+\left({\frac {d^{2}z}{ds^{2}}}\right)_{0}^{2}}}}\,

Den punkt på principalnormalen som ligger på avståndet R från kurvan kallas krökningscentrum och kan i vektorform anges som

\mathbf {r} =\mathbf {r} _{0}+\left(R^{2}{\frac {d^{2}\mathbf {r} }{ds^{2}}}\right)_{0}=\mathbf {r} _{0}+R\mathbf {n} \,

Ytor i R³

En yta i R³ kan skrivas i parameterform

x=x(u,v)\,

y=y(u,v)\,

z=z(u,v)\,

eller i vektorform

\mathbf {r} =\mathbf {r} (u,v)\,

Ekvationen kan också vara given på formen

F(x,y,z)=0\,

eller

z=f(x,y)\,

I det senare fallet kan x och y betraktas som parametrar, varvid ekvationen i parameterform blir:

{\begin{aligned}x&=u\\y&=v\\z&=f(u,v)\,\end{aligned}}

Linjeelement

{\begin{aligned}d\mathbf {r} ^{2}&=ds^{2}=dx^{2}+dy^{2}+dz^{2}=\\&=\left[1+\left({\frac {\partial z}{\partial x}}\right)^{2}\right]dx^{2}+2{\frac {\partial z}{\partial x}}{\frac {\partial z}{\partial y}}dx\,dy+\left[1+\left({\frac {\partial z}{\partial y}}\right)^{2}\right]dy^{2}\,\end{aligned}}

Tangentplanets ekvation

Om ekvationen för ytan är

F(x,y,z)=0\,

kan tangentplanets ekvation skrivas om tangeringspunkten är (x₀, y₀, z₀):

(x-x_{0})F_{x_{0}}'+(y-y_{0})F_{y_{0}}'+(z-z_{0})F_{z_{0}}'=0\,

eller i vektorform som

(\mathbf {r} -\mathbf {r} _{0})({\text{grad}}\,F)_{0}=0\,

Ytnormalens ekvation

Om ytans ekvation är

F(x,y,z)=0\,

så gäller för ytnormalen i punkten (x₀, y₀, z₀):

{\frac {x-x_{0}}{F_{x_{0}}'}}={\frac {y-y_{0}}{F_{y_{0}}'}}={\frac {z-z_{0}}{F_{z_{0}}'}}\,

eller

\mathbf {r} -\mathbf {r} _{0}=\lambda ({\text{grad}}\,F)_{0}\,

Se även

Referenser

^ Percey Franklyn Smith, Arthur Sullivan Gale (1905)Introduction to Analytic Geometry, Athaeneum Press
^ William H. McCrea, Analytic Geometry of Three Dimensions Courier Dover Publications, Jan 27, 2012

Externa länkar

Wikimedia Commons har media som rör Analytisk geometri.
Bilder & media

[intro-1] Percey Franklyn Smith, Arthur Sullivan Gale (1905)Introduction to Analytic Geometry, Athaeneum Press

[2] William H. McCrea, Analytic Geometry of Three Dimensions Courier Dover Publications, Jan 27, 2012

[1]

[2]

FAIR and interactive data graphics from a scientific knowledge graph

Koordinatsystem

Analytisk geometri i R2

Koordinatsystem och transformationer

Parallellförskjutning

Rotation

Avståndet mellan två punkter

Arean av en triangel

Delning av en sträcka

Vinkelkoefficienten för en rät linje

Räta linjens ekvation

k-formen

Interceptformen

Normalformen

Avståndet från en punkt till en rät linje

Enpunktsformen

Tvåpunktsformen

Vinkeln mellan två linjer

Plana kurvor

Tangenten

Asymptoter

Analytisk geometri i R3

Koordinatsystem

Rätvinkliga koordinater

Riktningscosiner

Vinkeln mellan två riktningar

Rotation av koordinatsystem

Avståndet mellan två punkter

Plan i R3

Normalform

Vektorform

Avståndet från en punkt till ett plan

Vinkeln mellan två plan

Räta linjen

Kurvor i R3

Båglängd

Tangent

Normalplanet

Oskulerande planet

Principalnormal

Krökningsradie

Ytor i R3

Linjeelement

Tangentplanets ekvation

Ytnormalens ekvation

Se även

Referenser

Externa länkar

Analytisk geometri i R²

Analytisk geometri i R³

Plan i R³

Kurvor i R³

Ytor i R³