FAIR and interactive data graphics from a scientific knowledge graph

Viteza sunetului este o mărime care descrie propagarea sunetului printr-un mediu ca unde sonore. Această viteză depinde de proprietățile mediului de propagare, în particular de elasticitatea și densitatea acestuia.

În fluide (gaze și lichide) participă la propagarea sunetului numai deformarea volumică a mediului; la solide mai intervin și forțele de forfecare. Formulele generale pentru viteza sunetului în aceste tipuri de mediu sunt:

Mediu	Formulă	Variabile
Gaze și lichide	$c_{\mathrm {fluid} }={\sqrt {\frac {K}{\rho }}}$	$K=-V{\frac {\partial P}{\partial V}}$ este modulul de elasticitate volumic, adiabatic $\rho$ este densitatea fluidului
Solide	$c_{\mathrm {solid} }={\sqrt {\frac {E}{\rho }}}$	$E$ este modulul lui Young $\rho$ este densitatea solidului

În gaze

Termodinamic, viteza sunetului în gaze este dată de relația:^[1]

c={\sqrt {\gamma R_{M}T}}

unde $\gamma$ este coeficientul de transformare adiabatică,

R M

este constanta caracteristică a gazului,

T

este temperatura, în K.

Pentru aer, $\gamma =1,4\,,$ $R_{M}=287$ J/kg K. La temperatura normală $T$ ₀ = 273,15 K (0 °C) viteza sunetului este:

c_{\mathrm {aer} ,0}={\sqrt {1,4\cdot 287\cdot 273,15}}=331,3

m/s

Dacă se consideră că variația cu temperatura a coeficientului de transformare adiabatică este nulă, relația de mai sus pentru aer devine:

c_{\mathrm {aer} }=331,3{\sqrt {\frac {T}{T_{0}}}}=331,3{\sqrt {1+{\frac {t}{273,15}}}}

m/s

unde $t$ este temperatura, în °C.

Numărul lui Mach

Articol principal: Număr Mach.

Mach (pronunție /mah/, după numele fizicianului austriac Ernst Mach) este o unitate de măsură folosită în aerodinamică pentru a exprima viteza unui corp care se deplasează într-un fluid: proiectil, avion, rachetă etc. Viteza Mach 1 este egală cu viteza sunetului în fluidul respectiv; în condiții standard Mach 1 este egal cu 1224 km/h (sau 340 m/s).

Numărul lui Mach este o mărime adimensională care arată de câte ori este mai mare viteza unui mobil decât viteza sunetului în acel mediu. Valorile subunitare ale numărului lui Mach înseamnă viteze subsonice (mai mici decât viteza sunetului), iar valorile supraunitare înseamnă viteze supersonice. O clasificare mai detaliată definește în plus vitezele transsonice (între Mach 0,8 și Mach 1,2) și vitezele hipersonice (mai mari de Mach 5).

În lichide

Viteza sunetului în lichide este mai mare decât în gaze, pentru că densitatea este mai mare (ceea ce ar însemna o inerție mai mare deci o viteză inferioară), compresibilitatea lichidelor este mult mai mică decât a gazelor, ceea ce face ca o perturbație a presiunii într-un punct să se propage rapid la punctele vecine. Astfel, în aer viteza sunetului este de 330-350 m/s, iar în apă este de aproximativ 1500 m/s.

Cunoașterea precisă a vitezei sunetului în apă este importantă într-o serie de domenii precum cartografierea acustică a fundului oceanic, aplicații ale sonarului subacvatic, comunicații etc. Viteza sunetului în apă depinde de o serie de parametri:

presiune (deci și adâncime);
temperatură: aproximativ 4 m/s la 1 °C;
salinitate: aproximativ 1 m/s la 1‰.

Modul în care se comportă această dependență este complicat, de aceea practic se folosesc formule empirice.^[2] O astfel de formulă, suficient de simplă și de precisă, este cea propusă de Kenneth V. Mackenzie în 1981:^[3]

c(t,s,z) = a₁ + a₂t + a₃t² + a₄t³ + a₅(s - 35) + a₆z + a₇z² + a₈t(s - 35) + a₉tz³,

unde t este temperatura în grade Celsius, s este salinitatea în părți la mie, iar z este adîncimea în metri. Cei nouă coeficienți a₁, a₂, ..., a₉ sînt:

a₁ = 1448,96; a₂ = 4,591; a₃ = -5,304×10^-2; a₄ = 2,374×10^-4; a₅ = 1,340; a₆ = 1,630×10^-2; a₇ = 1,675×10^-7; a₈ = -1,025×10^-2; a₉ = -7,139×10^-13

Pentru parametrii t = 25 °C, s = 35‰ și z = 1000 m se obține valoarea vitezei c = 1550,744 m/s. Eroarea de calcul a vitezei în limitele obișnuite ale parametrilor este de sub 0,2 m/s.

În solide

Într-o bară a cărei secțiune este mult mai mică decât lungimea de undă a sunetului viteza de propagare depinde de modulul lui Young și de densitatea solidului:

c_{\mathrm {solid} }={\sqrt {\frac {E}{\rho }}}

De exemplu, într-o bară de oțel viteza sunetului este de aproximativ 5100 m/s.

Când dimensiunile transversale ale mediului devin comparabile cu lungimea de undă această formulă nu mai este corectă, viteza reală fiind mai mare. Pentru o bară cu secțiunea transversală mult mai mare decât lungimea de undă modulul lui Young trebuie înlocuit cu modulul undei plane, M, care se poate calcula din modulul lui Young și coeficientul lui Poisson, $\nu$ :

M=E{\frac {1-\nu }{1-\nu -2\nu ^{2}}}

Viteza de propagare a sunetului calculată astfel este mai mare. De exemplu oțelul are un coeficient Poisson de aproximativ 0,3, ceea ce face ca viteza sunetului într-un bloc de oțel să fie de aproximativ 5900 m/s.

Viteza maximă teoretică a sunetului

Cercetători de la Universitate Regina Maria din Londra (Queen Mary University of London) au publicat în octombrie 2021 rezultatul unor cercetări efectuate în colaborare cu Universitatea din Cambridge și Institutul pentru Fizica Presiunilor Înalte din Troitsk, în urma cărora au emis ipoteza că limita superioară teoretică a vitezei sunetului se situează în jurul valorii de 36 kilometri pe secundă, de circa două ori mai mare decât viteza sunetului în diamant, substanța naturală cu cea mai mare duritate. Se presupune că această viteză maximă ar putea fi atinsă în hidrogenul metalic (hidrogen atomic solid), care poate exista numai la presiuni ce depășesc 1 milion de atmosfere.^[4]

Cazul deplasării sursei sonore

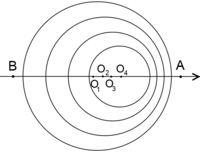
Când izvorul sonor (presupus punctiform) este în repaus, undele sonore care pornesc din acest punct sunt sferice, fronturile de undă fiind suprafețe sferice concentrice. În cazul în care sursa sonoră se mișcă (să presupunem rectiliniu), centrele suprafețelor sferice se vor găsi pe linia care reprezintă traiectoria sursei. În funcție de viteza sursei în raport cu viteza de propagare a sunetului, avem trei situații:

Viteza u a sursei sonore este mai mică decât viteza sunetului v.

Undele sonore nu mai sunt concentrice, dar se aglomerează în sensul propagării sursei de sunet. În acest caz, pentru un observator A, aflat în fața mobilului, frecvența sunetului pare mai ridicată (efectul Doppler), lucru invers în cazul unui observator B aflat în spatele mobilului.

Viteza u a undei sonore este egală cu viteza sunetului v.

Undele sferice au întotdeauna un punct comun, iar un observator aflat în direcția spre care se mișcă sursa recepționează toate undele sonore sub forma unui pocnet (bang-ul sonic).

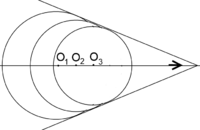
Viteza u a undei sonore mai mare decât viteza sunetului v.

Undele sferice se intersectează, iar înfășurătoarea acestora este un con cu vârful pe direcția de deplasare, în fața sursei. Unghiul $\varphi \!$ dintre generatoarea conului și direcția de deplasare este dat de:

\sin \varphi ={\frac {v\Delta t}{u\Delta t}}={\frac {v}{u}}.\!

Așadar, în cazul vitezei supersonice, un observator aflat în fața sursei sonore care se deplasează va recepta undele în sensul invers producerii acestora. Prin comprimarea aerului în direcția de înaintare, se generează o undă care nu are un caracter periodic, reprezentând doar un domeniu de comprimare care se propagă cu viteza sunetului. O astfel de undă se numește undă de șoc sau undă balistică. Ele provoacă senzația unui șoc puternic. Aceste unde apar de exemplu, în cazul proiectilelor sau al avioanelor cu reacție.

Vezi și

Note

^ Dan Ștefănescu (coord.) ș.a., Lexicon de termodinamică și mașini termice, Vol. IV (S–Z), București: Editura Tehnică, 1991, p. 270
^ en UK National Measurement Laboratory: „Speed of sound in sea-water” (o serie de formule empirice pentru viteza sunetului în oceanului)
^ en Kenneth V. Mackenzie, „Nine-term equation for sound speed in the oceans,” Journal of the Acoustical Society of America, Vol. 70, Nr. 3, septembrie 1981, pp. 801-806 PDF^{[nefuncțională]}
^ Scientists find upper limit for the speed of sound

Bibliografie

V. Kirillin, V. Sîcev, A. Șeindlin, Termodinamica, Editura Științifică și Enciclopedică, 1985, (traducere din limba rusă), p.293-297

[1] Dan Ștefănescu (coord.) ș.a., Lexicon de termodinamică și mașini termice, Vol. IV (S–Z), București: Editura Tehnică, 1991, p. 270

[2] UK National Measurement Laboratory: „Speed of sound in sea-water” (o serie de formule empirice pentru viteza sunetului în oceanului)

[3] Kenneth V. Mackenzie, „Nine-term equation for sound speed in the oceans,” Journal of the Acoustical Society of America, Vol. 70, Nr. 3, septembrie 1981, pp. 801-806 PDF^{[nefuncțională]}

[4] Scientists find upper limit for the speed of sound

[1]

[2]

[3]

[4]