FAIR and interactive data graphics from a scientific knowledge graph

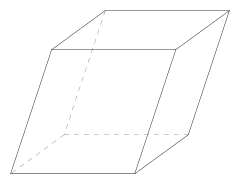
Suuntaissärmiö

Tyyppi	Monitahokas
Sivuja	6 suunnikasta
Särmiä	12
Kärkiä	8
Symmetriaryhmä	Syklinen symmetria C_i
Ominaisuuksia	kupera

Suuntaissärmiö (suunnikassärmiö eli parallelepipedi^[1]) on kuusitahkoinen monitahokas, jonka tahkot ovat suunnikkaita.

Suuntaissärmiöllä on kahdeksan kärkipistettä ja kaksitoista särmää. Särmät muodostavat kolme ryhmää, joissa kussakin on neljä keskenään yhdensuuntaista ja yhtä pitkää särmää. Vastakkaiset tahkot ovat yhdensuuntaiset. Suuntaissärmiö on särmiö, jossa mitkä tahansa kaksi vastakkaista tahkoa voidaan tulkita pohjiksi ja muut neljä tahkoa sivutahkoiksi.

Suuntaissärmiön erikoislajeja ovat suorakulmainen särmiö, jonka sivut ovat suorakulmioita, romboedri, jonka sivut ovat neljäkkäitä, sekä kaikkein säännöllisimpänä kuutio, jonka sivut ovat neliöitä.

Suuntaissärmiön avaruuslävistäjät leikkaavat toisensa samassa pisteessä, joka on suuntaissärmiön symmetriakeskus. Erikoistapauksia lukuun ottamatta suuntaissärmiöllä ei ole symmetria-akselia eikä symmetriatasoa, mutta jokaisella tahkolla on symmetriakeskus.

Tilavuus

Suuntaissärmiön tilavuus saadaan kertolaskulla Ah, jossa A on jonkin tahkon (kannan) pinta-ala ja h on särmiön korkeus eli kyseisen tahkon kohtisuora etäisyys vastakkaisesta tahkosta (ks. kuva).

Tilavuus skalaarikolmitulon avulla

Suuntaissärmiön tilavuus voidaan myös laskea käsittelemällä sen yhdestä kärkipisteestä alkavia, erisuuntaisia särmiä vektoreina:

a = (a₁, a₂, a₃), b = (b₁, b₂, b₃) ja c = (c₁, c₂, c₃).

Tällöin suuntaissärmiön tilavuus on sama kuin näiden vektorien skalaarikolmitulon itseisarvo:

V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|=|\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )|=|\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )|

Näin on, koska jos b ja c muodostamaa sivua käytetään kantana, on näiden sivujen muodostaman suunnikkaan pinta-ala yhtä suuri kuin vastaavien vektorien ristitulo, joka määritelmän mukaan on

A = |b| |c| sin θ = |b × c|,

missä θ on sivujen b välinen kulma.

Suuntaissärmiön korkeus taas on

h = |a| cos α,

missä α on sivun a ja sitä vastaan kohtisuoran korkeussuunnan h välinen kulma. Ristitulon määritelmän mukaan tämä korkeussuunta on samalla ristitulovektorin $b\times c$ suunta.

Tästä seuraa edelleen, että tilavuus

V = Ah = |a| |b × c| |cos β|,

mikä vektorien pistetulon määritelmän mukaan on yhtä suuri kuin a · (b × c).

Tilavuus determinantin avulla

Jos suuntaissärmiön sivut komponenttimuodossa ilmoitettuina vektoreina ovat a = (a₁, a₂, a₃), b = (b₁, b₂, b₃) ja c = (c₁, c₂, c₃), on suuntaissärmiön tilavuus yhtä suuri kuin näistä muodostetun matriisin determinantin itseisarvo :

V=\left|\det {\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{bmatrix}}\right|=|a_{1}b_{2}c_{3}+a_{2}b_{3}c_{1}+a_{3}b_{1}c_{2}-a_{1}b_{3}c_{2}-a_{2}b_{1}c_{3}-a_{3}b_{2}c_{1}|

.

Yksinkertaisimmassa tapauksessa sivut a, b ja c ovat koordinaattiakselien suuntaisia, jolloin kyseessä on suorakulmainen särmiö. Tällöin näistä komponenteista kaikki muut paitsi a₁, b₂ ja c₃ ovat nollia, jolloin tämä lauseke yksinkertaistuu muotoon

V=\left|a_{1}b_{2}c_{3}\right|

eli suorakulmaisen särmiön tilavuus saadaan kertomalla sen erisuuntaisten särmien pituudet keskenään.

Lähteet

↑ Otavan iso Fokus, 5. osa (Ra-Su), art. Suunnikassärmiö, Kustannusosakeyhtiö Otava, 1974, ISBN 951-1-00050-0

Aiheesta muualla

Kuvia tai muita tiedostoja aiheesta Suuntaissärmiö Wikimedia Commonsissa

[1] Otavan iso Fokus, 5. osa (Ra-Su), art. Suunnikassärmiö, Kustannusosakeyhtiö Otava, 1974, ISBN 951-1-00050-0

[1]