FAIR and interactive data graphics from a scientific knowledge graph

Dimentsioa (latineko dimetiri 'neurtu' eta honen abstrakzio den dimensiō hitzetik dator) objektu matematiko baten ezaugarri metriko edo topologikoei lotutako “zenbakia” da. Dimentsioaren kontzeptu abstraktuenak espazioan mugimendu bat egiteko zenbat askatasun-gradu dauden islatu nahi du.  Askatasun-gradu horien kopurua litzateke, hain zuzen, dimentsioa.

"Dimentsio" terminoa; irudi geometriko edo objektu fisiko baten neurri linealaren balioa adierazteko ere erabiltzen da, nahiz eta zentzu horrek ez duen erlaziorik dimentsioaren kontzeptu abstraktuenarekin. Izan ere, dimentsio terminoak definizio desberdinak izan ditzake arloaren arabera, aurrerago jorratuko direnak.  

Fisikan eta matematikan, espazio matematiko (edo objektu) baten dimentsioa haren barruan edozein puntu zehazteko behar den gutxieneko koordenatu-kopurua da^[1][2]. Hortaz,

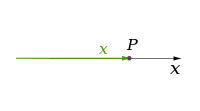
• Zuzen batek bateko dimentsioa du (1D), koordenatu bakarra behar baita puntu bat zehazteko.

• Gainazal batek, zilindro edo esfera baten mugak, adibidez, biren dimentsioa du (2D), bi koordenatu behar baitira bertan puntu bat zehazteko; adibidez, latitudea eta longitudea behar dira esfera baten azalean puntu bat kokatzeko.

• Kubo, zilindro edo esfera baten barrualdea hiru dimentsiokoa da (3D), hiru koordenatu behar baitira espazio horien barruan puntu bat kokatzeko.

• Kasu konplexuagoetan, hala nola dimentsio fraktalean edo multzo abstraktuen dimentsio topologikoan, koordinatuen kopuruaren nozioa ez da aplikagarria, eta kasu horietan dimentsio kontzeptuaren definizio formalak erabili behar dira.

• Mekanika klasikoan, espazioa eta denbora kategoria desberdinak dira, eta espazioari eta denbora absolutuari dagozkie. Espazio-denboraren lau dimentsioak (4D) espazio eta denboraren arabera guztiz definituta ez dauden gertaeretan dautza; izan ere,  behatzaile baten mugimenduarekin lotuta daude.

• Hamar dimentsio erabiltzen dira superkorden teoria deskribatzeko (6D hiperespazioa + 4D) eta hamaika dimentsiok supergrabitatea eta M teoria deskriba dezakete (7D hiperespazioa + 4D).

• Mekanika kuantikoaren egoera-espazioa dimentsio infinituko espazio-funtzioa da.

Dimentsio kontzeptua ez da objektu fisikoetara mugatzen. "Dimentsio handiko espazioak" ohikoak dira matematikan eta zientzietan. Hauek espazio euklidearrak edo espazio parametriko orokorragoak izan daitezke, edota Lagrangeren mekanika edo mekanika hamiltondarra bezalako konfigurazio-espazioak; hauek guztiak espazio abstraktuak dira, bizi garen espazio fisikoarekin zerikusirik ez dutenak.

Matematikan, objektu baten dimentsioa, gutxi gorabehera, objektu horren gainean mugitzen den puntu baten askatasun-graduen kopurua da. Bestela esanda, dimentsioa da objektuan egotera mugatuta dagoen puntu baten posizioa definitzeko behar diren parametro edo koordenatu independenteen kopurua. Adibidez, puntu baten dimentsioa zero da; lerro baten dimentsioa bat da, puntu bat norabide bakarrean mugi daitekeelako (edo kontrako norabidean); plano baten dimentsioa bi da, etab.

Dimentsioa objektu baten berezko propietate bat da, objektua sartuta dagoen edo egon daitekeen espazioaren dimentsioarekiko independentea baita. Adibidez, kurba bat 1 dimentsiokoa da, puntu batek kurba batean duen posizioa zehazteko kurban zeharreko  puntu finko bateraino duen distantzia hartzen baita kontuan.

Tesseract bat lau dimentsioko objektu baten adibidea da. Matematikatik kanpo, "dimentsio" terminoaren erabilera "Tesseract batek lau dimentsio ditu" esaldian islatzen da; matematikariek, berriz, hau adierazten dute eskuarki: "Tesseractak 4 dimentsio ditu", edo "Tesseractaren dimentsioa 4 da" edo "4D".

Dimentsio handiagoen nozioa René Descartesena izan zen arren, geometria matematikoko  dimentsioaren funtsezko garapena XIX. mendean hasi zen, Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli eta Bernhard Riemann-en lanaren bidez. Habilitationsschrift, Riemann-en 1852-ko Theorie der viellote Kontinuität lanek , eta Hamiltonen kuaternioien aurkikuntzak eta John T. Gravesek oktonioiei buruz 1843an egindako aurkikuntzak dimentsio handiko geometriaren hasiera markatu zuten.

Atal honetan dimentsioari buruzko definizio matematiko garrantzitsuenak aztertzen dira.

Gorputz baten gaineko espazio bektorialak n dimentsioa duela esaten da n kardinala duen oinarria badu.  Espazio bektorial batean, oinarri guztiek kardinal bera dute, eta horrek aljebra linealaren lehen inbariantea bihurtzen du dimentsioa. Intuizioz hitz eginez, espazio bektorial baten dimentsioak esaten digu zenbat elementu behar ditugun espazioko edozein elementu adierazteko; lehenengoen konbinazio linealen arabera, hau da, espazioaren zenbat elementu behar ditugun espazioko elementu guztiak elementu horien multiploen batura gisa adierazteko. Dimentsio finituko espazio bektorialak oso ohikoak dira zientziaren arlo askotan, baina matematika eta fisika kuantikoan dimentsio infinituko espazio bektorialen kasu garrantzitsuak ere agertzen dira.

Puntu batez osatutako espazio baterako, dimentsio topologikoa 0 da, zuzen errealerako 1, plano euklidearrerako 2, eta abar.

Formalki idatzita, objektu batek m dimentsio topologikoa du; objektu horren edozein estaldurak gutxienez dimentsio topologiko bat duenean = m+1 (aldez aurretik puntuak dimentsio topologikoa = 0 duela ezarriz).

Are formalago, 0 dimentsio topologikoa duten multzoen definizioa hau da: F multzo batek 0 dimentsio topologikoa, , duela esaten da baldin eta soilik baldin F-ren x orotarako eta U-ren edozein multzo irekirentzat (F-ren topologia erlatiborako) a x duen edozein multzotarako, V ireki bat badago, non x  V-koa den eta V-ren eta F-ren elkargunearen arteko muga hutsik baitago.

Aldaera aljebraiko baten dimentsioa zenbait forma baliokidetan defini daiteke. Forma intuitiboena, seguruenik,  espazio ortogonalaren dimentsioa da, aldaera aljebraiko baten edozein gune erregularretan.Beste modu intuitibo bat dimentsioa definitzeko honako hau da: hiperplanoak eta barietateak duten ebakidura dimentsioko puntu kopuru mugatu batera murrizteko behar diren hiperplano kopurua da.Definizio hori honako honetan oinarritzen da: barietate baten eta hiperplano baten ebakidurak dimentsio bat txikitzen da barietatea hiperplanoaren barruan badago

Multzo aljebraiko bat barietate aljebraikoen bildura finitua izanik, bere  dimentsioa barietate aljebraiko hoien dimentsioetatik maximoa da. Emandako multzo aljebraikoaren azpi-barietate kateen V0⊊V1⊊…⊊Vd luzera maximoaren berdina da (kate horren luzera ⊊ kopurua da).

Barietate bakoitza pila aljebraikotzat har daiteke, eta barietate gisa duen dimentsioarekin bat dator. Hala ere, pila aljebraiko asko ez datoz bat barietateekin, eta horietako batzuek dimentsio negatiboa dute. Zehazki, V m dimentsioko barietatea bada eta G n dimentsioko talde aljebraikoa bada, orduan [V/G] zatiduraren pilak m–n dimentsioa du^[3].

Dimentsio hori Kolmogóroven entropiarekin edo Minkowski Bouligand-en dimentsioarekin nahastu izan da. Hausdorff-Besicovitch-en dimentsioa Hausdorff-en luzeran aukeratutako potentziaren balioaren inflexio-puntu gisa lortzen da, potentzia infinitua izatetik nulua izatera pasatzen denean. Hausdorff-en luzera da objektuaren estaldura osoaren "s" potentzia batera igotzen den diametro topologikoaren batura, delta-diametroa edo objektuaren beraren diametroa baino txikiagoa duten inguruneetatik edo estalduretatik abiatuta.

Hilberten espazio bakoitzak oinarri ortonormal bat onartzen du, eta bi oinarri hauetako edozeinek kardenalitate bera du espazio jakin baterako. Ezaugarri horri Hilbert espazioaren dimentsioa deitzen zaio. Dimentsio hori mugatua da baldin eta espazioko Hamelen dimentsioa mugatua bada, eta, kasu horretan, bi dimentsioak berdinak badira.

Kolmogóroven entropia deitzen zaio kalkuluak erraz egiteko lortutako dimentsioari, hala nola eraldaketagatik objektu batean aurkitutako barne-homotezien kopuruaren eta homotezia horren arrazoiaren alderantzizkoaren arteko zatidura logaritmikoa. Kutxen zenbaketa bidezko dimentsioa ere esaten zaio, eta definizio intuitiboagoa du, baina luzeagoa horri dagokionez.

Horrela, bada, objektu euklidear bereizgarriek bat egiten dute balio dimentsional topologikoan, kaxen kontaketaren dimentsioan eta Hausdorff-Besicovitch-en dimentsioan. Hori ez da gertatzen fraktalekin, non Benoit Mandelbrot-ek honela definitzen baititu:

Hausdorff - Besicovitch-en dimentsioa bere dimentsio topologikoa baino zorrotzagoa duten objektuak.

Azkenik, badakigu zenbait fraktal ez direla definizio horretan sartzen; horietako bat deabruaren kurba da, Cantor-en multzotik eratorritako fraktala.

Eraztun konmutatibo baten Krull dimentsioa eraztuneko ideal nagusien kateen luzera maximoa da, n luzera-kate bat, inklusioarekin lotutako ideal lehenen  sekuentzia bat izanik. Oso lotuta dago aldaera aljebraiko baten tamainarekin, polinomioen eraztunaren azpibarietate eta ideal lehenen arteko korrespondentzia naturalari esker.

Gorputz baten gaineko aljebra baterako, dimentsioa espazio bektorial gisa mugatua da baldin eta Krull dimentsioa 0 bada soilik.

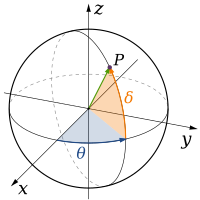
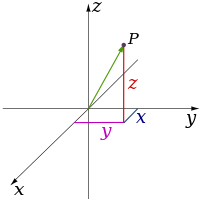
Fisikako teoria klasikoek hiru dimentsio fisiko deskribatzen dituzte: espazioaren puntu jakin batetik mugitzeko oinarrizko norabideak gora/behera, ezkerrera/eskuinera eta aurrera/atzera dira. Beste edozein norabidetako mugimendua hiru norabide horietan oinarrituta adieraz daiteke. Beherantz mugitzea eta gorantz distantzia negatiboarekin mugitzea gauza bera dira. Diagonalean gorantz eta aurrerantz mugitzea, norabidearen izenak adierazten duen bezala, gora eta aurrera mugitzearen konbinazio lineala da. Forma sinpleenean: lerro batek dimentsio bat deskribatzen du, plano batek bi dimentsio deskribatzen ditu eta kubo batek hiru dimentsio deskribatzen ditu. (Ikus Espazioa eta koordenatu kartesiarren sistema).

Dimentsio zenbakia	Sistema koordenatuen adibideak
1	Zuzena Angelua
2	Kartesiarra Polarra Latitudea eta longitudea
3	Kartesiarra Ziklikoa Esferikoa

Denbora dimentsioa denbora aldagaiari dagokion dimentsioa da, alegia, denboraren aldaketaren dimentsioa. Arrazoi horregatik, askotan, denbora kontzeptua hartzen da espazioaren laugarren dimentsiotzat, baina horrek ez du esan nahi dimentsio espaziala denik. Denbora dimentsioa aldaketa fisikoa neurtzeko modu bat da. Alabaina, espazioko hiru dimentsioetan ez bezala, hemen dimentsio bakarra dago eta ezin gara denboran libreki mugitu, norabide batean mugitzen gara.

Fisikan errealitatea modelatzeko erabiltzen diren ekuazioek ez dute denbora hautematen gizakiek egiten duten moduan. Mekanika klasikoaren ekuazioak simetrikoak dira denborarekiko, eta mekanika kuantikoaren ekuazioak simetrikoak izan ohi dira, denbora eta beste kantitate batzuk (karga eta paritatea, esaterako) alderantzikatzen badira. Eredu horietan, denbora noranzko batean doala hautematea termodinamikaren legeen arrazoia da (denbora entropia handitzearen norabidean doala hautematen dugu).

Ouspenskyren arabera, laugarren dimentsioa, gizakientzat kontzeptu oso zaila dena, denboraren dimentsioa da. Ouspenskyk bere ikerketan erantzun zuen denbora dela ulertzeko  zailen egiten zaigun kategoria. Haren arabera, denbora zirkularra izango litzateke. Horregatik, dena errepikatzearen sentsazioa ziklikoa izan daiteke, ez bakarrik gizakiaren bizitzan, giza historian, historia biologikoan, planetenean, eguzkian eta, oro har, unibertsoan ere. Horrela ulertu zuen Ouspenskyk denboraren eta laugarren dimentsioaren izaera zirkularra.

Fisikan, espazioaren hiru dimentsio eta denboraren dimentsio bakarra da onartutako araua. Hala ere, badira oinarrizko lau indarrak batu nahi dituzten teoriak, dimentsio gehigarriak/hiperespazioa sartuz. Nabarmenago, superkorden teoriak 10 dimentsio espazial behar ditu, eta 11 dimentsioko teoria oinarrizkoago batetik sortzen da; behin-behinean M teoria deiturikoa eta aldez aurretik desberdinak diren bost superkorden teoria batzen dituenak. Supergrabitatearen teoriak, halaber, 11D espazio-denbora = 7D hiperespazioa + 4 dimentsio komun sustatzen ditu. Orain arte ez dago dimentsio gehigarri horiek badirela bermatzen duen ebidentziarik edo behaketa zuzenik. Hiperespaziorik existitzen bada, mekanismo fisikoren batek gure ezkutuan du. Dimentsio gehigarriak eskala txikitan "kiribilduta" bizi ahal izatea ondo aztertutako aukera bat da, egungo esperimentuetan benetan ikusezin izateko bezain eskala txikitan.

1921ean, Kaluza-Kleinen teoriak 5D aurkeztu zuen, espazioaren aparteko dimentsio bat barne zuena. Eremu-teoria kuantikoaren mailan, Kaluza-Kleinen teoriak grabitatea eta Gaugeren interakzioak bateratzen ditu, dimentsio txiki eta konpaktuetan hedatzen den grabitatea distantzia luzeetako Gaugen interakzioekin baliokidea dela ulertzean oinarrituta. Batez ere, dimentsio gehigarrien geometria hutsala denean, elektromagnetismoa erreproduzitzen du. Hala ere, energia nahiko altuetan edo distantzia laburretan, grabitate kuantikoa deskribatzeko zuzeneko saiakerak oztopatzen dituzten patologia berberak ditu konfigurazio horrek. Beraz, eredu horiek oraindik ere UV osotasun bat behar dute, harien teoriak eman nahi duen motakoa. Bereziki, superkorden teoriak sei dimentsio trinko eskatzen ditu (6D hiperespazioa), Calabi-Yau barietate bat osatuz. Beraz, Kaluza-Kleinen teoria, bakarrik, osatu gabeko deskribapentzat har daiteke, edo harien teoriaren ereduak eraikitzeko azpimultzotzat.

Neurri txiki eta kiribildutakoez gain, beste dimentsio batzuk ere egon litezke, baina ikusgaiak ez liratekeenak, gure unibertso ikusgaiarekin lotutako materia (3 + 1)-dimentsioko azpieremu batean  baitago. Beraz, neurri osagarriek ez dute txikiak eta trinkoak izan behar; aldiz, neurri gehigarri handiak ere izan litezke.

Artikulu nagusia: Unibertso paraleloak fikzioan.

Zientzia-fikzioan, batzuetan "dimentsio" terminoa unibertso paraleloaren sinonimo gisa erabiltzen da; nahiz eta “dimentsio” eta “mundu paralelo” terminoak erlazionatuta egon, ez dira sinonimoak (ikusi Korden teoria).

Zenbait sistema digital mota oinarritzen dira forma geometrikoak biltegiratzean, aztertzean eta bistaratzean oinarritzen dira, hala nola, ilustrazioko softwarea, ordenagailuz lagundutako diseinua eta Geografia-informazioko sistemak. Bektore-sistema desberdinek askotariko datu-egiturak erabiltzen dituzte formak irudikatzeko, baina ia guztiak espazio-dimentsioei dagozkien geometria primitiboko multzoan oinarritzen dira funtsean, hots, sistemak erabil ditzakeen forma geometriko sinpleenetan:

• Puntua (zero dimentsiokoa), koordenatu kartesiar sistema bateko koordenatu bakarra.
• Zuzena (bat dimentsiokoa). Normalean, lerro jarraitu batetik lagindutako puntuen zerrenda ordenatu gisa irudikatzen da, eta, beraz, softwareak zuzenaren forma lerro zuzen edo kurboko segmentu gisa interpolatuko duela espero da.
• Poligonoa (bi dimentsiokoa). Oro har, ertzetan ixten den zuzena da, eta bi dimentsioko eskualde baten muga adierazten du.  Softwareak muga hori erabiltzea espero da espazio bidimentsionala barnealde eta kanpoalde eremuetan banatzeko.
• Azalera (hiru dimentsiokoa), hainbat estrategia erabiliz irudikatua, hala nola poliedro bat, poligono-aurpegi konektatuak dituena. Softwareak gainazal hori erabiltzea espero da hiru dimentsioko espazioa barnealde eta kanpoalde eremuetan banatzeko.

Sarritan, sistema horietan, batez ere GIS (Geografia-informazioko sistemak) eta kartografian,  mundu errealeko fenomenoen irudikapen batek dimentsio desberdina (gehienetan txikiagoa) izan dezake irudikatzen den fenomenoak baino. Adibidez, hiri bat (bi dimentsioko eskualde bat) puntu gisa adieraz daiteke, edo errepide bat (77777 bolumena) lerro gisa. Dimentsio-orokortze hori espazio ezagutzaren joerekin lotzen da. Adibidez, bi hirien arteko distantzia galdetzeak hirien eredu kontzeptuala puntu gisa adierazten du; aldiz, errepide batean bidaiatzeko erabiltzen diren "gora", "behera" edo "zehar" motako jarraibideak emateak eredu kontzeptual dimentsiobakarra eskatzen du. Hori askotan egiten da datuen eta ikusmenaren eraginkortasunerako, edo eraginkortasun kognitiborako, eta onargarria da irudikapenaren eta irudikatutakoaren arteko bereizketa ulertzen bada. Hala ere,  nahasgarria izan daiteke informazioaren erabiltzaileek forma digitala errealitatearen irudikapen perfektua dela onartzen badute (esate baterako, errepideak benetan lerroak direla sinestea).

1. ↑ «Curious About Astronomy: What is a dimension?» web.archive.org 2014-01-11 (Noiz kontsultatua: 2023-11-29).
2. ↑ (Ingelesez) Weisstein, Eric W.. «Dimension» mathworld.wolfram.com (Noiz kontsultatua: 2023-11-29).
3. ↑ «Wayback Machine» web.archive.org (Noiz kontsultatua: 2023-11-29).