Effects of the storage conditions on the stability of natural and synthetic cannabis in biological matrices for forensic toxicology analysis: An update from the literature

Sistema de referencia
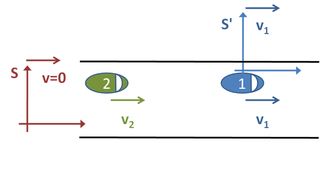
	sistema conceptual (es) , puntu de vista, modelo conceptual (es) y physical concept (en)

Un sistema de referencia o marcu de referencia ye un conxuntu de convenciones usaes por un observador pa poder midir la posición y otres magnitúes físiques d'un sistema físicu y de mecánica. Les trayectories midíes y el valor numbéricu de munches magnitúes son relatives al sistema de referencia que se considere, por esa razón, dizse que'l movimientu ye relativu. Sicasí, anque los valores numbéricos de les magnitúes pueden diferir d'un sistema a otru, siempres tán rellacionaos por rellaciones matemátiques tales que dexen a un observador predicir los valores llograos por otru observador.

En mecánica clásica frecuentemente úsase'l términu pa referise a un sistema de coordenaes ortogonales pal espaciu euclideu (daos dos sistemes de coordenaes d'esi tipu, esiste un xiru y una traslación que rellacionen les midíes d'esos dos sistemes de coordenaes).

En teoría de la relatividá mecánica relativista refierse usualmente al conxuntu de coordenaes espaciu-temporales que dexen identificar cada puntu del espaciu físicu d'interés y l'orde cronolóxicu de sucesos en cualquier eventu, más formalmente un sistema de referencia en relatividá puede definise a partir de cuatro vectores ortonormales (ún temporal y trés espaciales).

Introducción

Mecánica newtoniana

En física clásica un sistema de referencia cartesianu definir por un par (P, Y), onde'l primer elementu P ye un puntu de referencia arbitrariu, de normal perteneciente a un oxetu físicu, a partir del cual considérense les distancies y les coordenaes de posición. El segundu elementu Y ye un conxuntu d'exes de coordenaes. Les exes de coordenaes tienen como orixe de coordenaes nel puntu de referencia (P), y sirven pa determinar la direición del cuerpu en movimientu (o espresar al respective de ellos cualesquier otra magnitú física vectorial o tensorial).

Un tercer elementu ye l'orixe nel tiempu, un intre a partir del cual mídese'l tiempu. Esti intre acostuma a coincidir con un sucesu concretu. En cinemática l'orixe temporal coincide davezu col entamu del movimientu que s'estudia.

Estos trés elementos: puntu de referencia, exes de coordenaes cartesianos y orixe temporal, formen el sistema de referencia. Pa poder utilizar un sistema de referencia, sicasí, precísense unes unidaes de midida que nos sirvan pa midir. Les unidaes son convencionales y defínense tomando como referencia elementos físicamente constantes. A un conxuntu d'unidaes y les sos rellaciones llámase-y sistema d'unidaes. Nel Sistema Internacional d'Unidaes o SI, utilízase'l metro como unidá del espaciu y el segundu como unidá del tiempu.

Si un oxetu mover en llinia recta, solamente ye necesariu una exa pa describir el so movimientu. Cuando se mueve por un planu faen falta siquier dos exes. Pa movimientos nel espaciu utilicen trés exes. Les coordenaes más utilizaes son les coordenaes cartesianes, designaes (x,y,z), onde x ye la proyeición sobre'l "exa horizontal" (x ye positivu escontra la derecha y negativu escontra la esquierda); y ye la coordenada vertical, positivu escontra riba y negativu escontra baxo; y z mide la fondura, positivu cuando s'avera y negativu cuando s'alloñar. Cuando s'estudien movimientos al respective de la superficie de la Tierra, acostumar a faer pasar la exa y o la exa z pel centru de la Tierra, col orixe de coordenaes asitiáu na superficie.

Daos dos sistemes de referencia R₁ y R₂, con un orixe de tiempos y que se mueven con una velocidá constante unu respectu al otru, les coordenaes de dambos sistemes de coordenaes tán rellacionaos por aciu:

${\begin{pmatrix}x_{2}\\y_{2}\\z_{2}\end{pmatrix}}={\begin{bmatrix}r_{xx}&r_{xy}&r_{xz}\\r_{yx}&r_{yy}&r_{yz}\\r_{zx}&r_{zy}&r_{zz}\end{bmatrix}}{\begin{pmatrix}x_{1}-x_{0}-v_{x}t\\y_{1}-y_{0}-v_{y}t\\z_{1}-z_{0}-v_{z}t\end{pmatrix}}$

Onde:

r_{ij}\,

, son les componentes d'una matriz ortogonal que representa la rotación necesaria pa dar a los dos sistemes la mesma orientación.

v_{i}\,

, son les componentes de la velocidá del sistema 1 respectu al 2.

(x_{0},y_{0},z_{0})\,

, ye la posición del orixe de coordenaes 2 respectu al orixe de coordenaes de 1 nel intre t = 0.

Mecánica clásica lagrangiana

En mecánica clásica lagrangiana tamién ye interesante usar sistemes de referencia más complicaos, definíos por un conxuntu de coordenaes curvillinies nel espaciu. Les coordenaes de les magnitúes vectoriales o tensoriales nestos sistemes de referencia non cartesianos defínense al respective de los vectores tanxentes a les llinies coordenaes en cada puntu. Dau un conxuntu de coordenaes curvillinies $\scriptstyle \mathbf {q} =(q^{1},\dots ,q^{n})$ en cada'l sistema de "exes" vien dau por:

$Y=\left\{{\frac {\partial }{\partial q^{1}}},\dots ,{\frac {\partial }{\partial q^{n}}}\right\}$

Un sistema de cartesianu de referencia ye unu en que $\scriptstyle \mathbf {q} =(x,y,z)$ y l'orixe de referencia vien dau por $\scriptstyle \mathbf {q} =(0,0,0)$ .

Mecánica relativista

La definición de sistema de referencia en relatividá ye más complexa, yá que polo xeneral nun puede establecese un orixe de tiempos válidu pa cualquier observador con independencia del puntu del espaciu en que s'atope. En principiu un sistema de referencia queda definíu en relatividá especificando un conxuntu d'observadores partíos primeramente por una hipersuperficie del espaciu tiempu. Hai sistemes que llamaos sincronizables que si dexen establecer un orixe de tiempos común, pero esos sistemes namái pueden esistir nun espaciu-tiempu estacionariu. Los problemes acomuñaos a la "relatividá del tiempu" obliguen a que la definición de sistema de referencia en teoría de la relatividá xeneral sía notoriamente más complicada qu'en mecánica clásica.

En relatividá xeneral defínese un sistema de referencia como un conxuntu d'observadores locales, esto ye, un sistema de referencia ye un campu vectorial que les sos curves integrales son observadores locales, esto ye, curves temporales.

Sistema inercial

A les traces, ye un sistema de referencia nel que les lleis físiques adopten una forma simplificada, equivalente a les lleis de Newton pa pequeñes velocidaes. Dau un sistema inercial, cualesquier otru sistema de referencia que tea paráu o bien que se mueva en llinia recta a velocidá constante respectu al primeru, ye tamién un sistema inercial.

Formalmente, en mecánica clásica y teoría de la relatividá especial, un sistema inercial ye aquel nel que los símbolos de Christoffel llograos a partir de la función lagrangiana anúlense. Nun sistema inercial nun son necesaries fuercies ficticies pa describir el movimientu de les partícules reparaes por aciu el conxuntu de convenciones que describen el sistema de referencia.

Ver tamién

Referencies

Enllaces esternos

Wikimedia Commons tien conteníu multimedia tocante a Sistema de referencia.

Sistema de referencia
sistema conceptual ^(es) , puntu de vista, modelo conceptual ^(es) y physical concept ^(en)