Type a search term to find related articles by LIMS subject matter experts gathered from the most trusted and dynamic collaboration tools in the laboratory informatics industry.
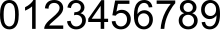
Le cifre indo-arabiche, talora note come numeri arabi o cifre arabe, sono la rappresentazione simbolica delle entità numeriche più comune al mondo. Sono considerati una pietra miliare nello sviluppo della matematica.
Si può distinguere tra il sistema posizionale utilizzato, conosciuto anche come sistema numerico indo-arabo, e il preciso glifo utilizzato. I glifi più comunemente usati in associazione all'alfabeto latino sin dai tempi dell'era moderna sono 1 2 3 4 5 6 7 8 9 0.
Un primo sistema numerico nacque in India tra il 400 a.C. ed il 400 d.C.[1][2] Furono trasmessi prima nell'Asia occidentale, dove trovano menzione nel IX secolo, ed in seguito in Europa nel X secolo.[1] Gli arabi assimilarono elementi di varie culture che conquistarono e forgiarono un sistema numerico arabo-indiano dal quale deriva quello arabo. La conoscenza di tali numeri raggiunse l'Europa attraverso il lavoro di matematici ed astronomi arabi, con un sistema numerico frutto dell'evoluzione del precedente e definito arabo o arabo occidentale. In Europa il sistema di numeri arabo occidentale venne chiamato a "numeri arabi".
In arabo, i numeri arabi orientali sono chiamati "numeri indiani" (in arabo أرقام هندية?, ’arqām hindiyya), e viene utilizzato lo stesso sistema, con glifi di forma diversa (٠١٢٣٤٥٦٧٨٩).
I simboli da 0 a 9 nel sistema numerico indo-arabico si evolsero dai numeri brahmi. Le iscrizioni buddiste intorno al 300 a.C. utilizzano i simboli che poi divennero 1, 4 e 6. Un secolo più tardi, fu registrato l'utilizzo dei simboli che poi divennero 2, 7 e 9.
L'iscrizione universalmente accettata come la prima contenente il glifo 0 è stata registrata per la prima volta nel IX secolo, a Gwalior risalente all'870. In ogni caso, prima di questa data, l'uso del glifo aveva già raggiunto la Persia, ed è menzionato nelle descrizioni di al-Khwārizmī sui numeri indiani. Documenti indiani su piatti di rame, con lo stesso simbolo per zero in essi, risalgono indietro fino al VI secolo d.C., in grande quantità.[3]
Del sistema numerico venne a conoscenza contemporaneamente il matematico persiano al-Khwārizmī (cui si deve il libro Sul calcolo con i numeri indù, scritto intorno all'825) e il matematico arabo al-Kindi, che scrisse quattro volumi Sull'utilizzo dei numeri indiani (Kitāb fī istiʿmāl al-ʿadad al-hindī) intorno all'830.
Questi scritti sono i principali responsabili della diffusione del sistema indiano di numerazione nel Vicino e Medio Oriente e nei Paesi occidentali.[2]
Nel X secolo, matematici vicino e medio-orientali estesero il sistema numerico decimale ad includere frazioni, così come registrato dal trattato del Kitāb al-Fuṣūl fī l-ḥisāb al-hindī, composto a Damasco nel 952/3 dal matematico Abū l-Ḥasan Aḥmad b. Ibrāhīm al-Uqlīdisī, rimasto inedito ma studiato da A. S. Saidan.
Nel mondo arabo, fino ai tempi moderni, il sistema numerico arabo era utilizzato solo dai matematici. Scienziati musulmani utilizzavano il sistema di numerazione babilonese, e i mercanti utilizzavano i numeri abjad. In Italia invece, con la diffusione delle opere di Leonardo Fibonacci, figlio del mercante pisano Guglielmo Bonacci, che aveva viaggiato sulle sponde del mediterraneo, il sistema numerico arabo cominciò a essere utilizzato da larghi strati della popolazione.
Una variante distintiva "araba occidentale" dei simboli incominciò ad emergere intorno al X secolo nel Maghreb e in al-Andalus. Essa chiamava i numeri ghubar ("tavola di sabbia" o "tavola di polvere").
Le prime menzioni dei numeri nei paesi occidentali sono trovate nel Codex Vigilanus del 976.[4] Nel decennio del 980, Gerberto di Aurillac (più tardi noto come Papa Silvestro II) iniziò a diffondere la conoscenza dei numeri in Europa. Gerberto aveva studiato nella sua giovinezza a Barcellona, ed è conosciuto per aver richiesto trattati matematici riguardanti l'utilizzo dell'astrolabio da Lupito di Barcellona dopo che ritornò in Francia.
Al-Khwārizmī, uno scienziato persiano della Transoxiana, scrisse nell'825 il trattato Sul calcolo con i numeri hindi, che fu tradotto in latino nel XII secolo. Del trattato sopravvivono soltanto alcuni riadattamenti in lingua latina[5], tra cui il celebre Algoritmi de numero Indorum, il cui titolo tradotto in italiano significa «Algoritmi sui numeri degli indiani»[6]. In latino “Algoritmi” era l'adattamento del nome dell'autore, ma i lettori per sbaglio lo intesero come il plurale latino dell'ipotetico termine Algoritmus: questo portò a coniare il termine algoritmo (dal latino algorithmus) che venne ad acquisire il significato di “metodo di calcolo”.
Leonardo Fibonacci, un matematico italiano che aveva studiato a Bijaya, in Algeria, promosse il sistema numerico arabo in Europa nel suo trattato Liber abbaci, che fu scritto nel 1202 e poi riedito nel 1228, e che ancora descriveva i numeri come "indiani" anziché "arabi":
«Quando mio padre, che era stato nominato dal suo paese pubblico notaio nelle dogane di Bugia facendo gli interessi dei mercanti pisani che andavano là, ivi vi lavorava, mi mandò a chiamare mentre ero ancora un fanciullo, e tenendo d'occhio l'utilità e la futura convenienza, espresse il desiderio di farmi restare e ricevere un'istruzione alla scuola di ragioneria. Là, dove fui introdotto all'arte dei nove simboli indiani attraverso un insegnamento ragguardevole, la conoscenza dell'arte ben presto mi piacque sopra ogni altra cosa ed io ebbi modo di comprenderla...»
I numeri sono disposti secondo l'uso arabo, con il loro più basso valore a destra, con le posizioni di valore più alte a sinistra. Questa disposizione fu adottata allo stesso modo anche dai numeri utilizzati in Europa. L'alfabeto latino scorrendo da sinistra verso destra, a differenza dell'alfabeto arabo, portò ad una disposizione invertita dei relativi piazzamenti di valore relativa alla direzione di lettura.
L'accettazione europea dei numeri fu accelerata dall'invenzione della stampa a caratteri mobili, e i numeri divennero comuni durante il XV secolo. Fra le prime attestazioni in Inghilterra si annoverano: un'iscrizione risalente al 1445 sulla torre della Chiesa di Heathfield, Sussex, un'iscrizione del 1448 su un cancello in legno della Chiesa di Bray Church, Berkshire, un'iscrizione del 1470 su una tomba del primo Conte di Huntly nella Cattedrale di Elgin e un'iscrizione del 1487 sulla porta campanaria della Chiesa di Piddletrenthide, nel Dorset. Nella metà del XVI secolo, erano comunemente usati nella maggior parte dell'Europa.[7]
I numeri romani rimasero in uso principalmente per la notazione degli anni dopo Cristo, e per i numeri dei quadranti di orologio. Alle volte, i numeri romani sono utilizzati per la numerazione di liste (come alternativa ad una numerazione alfabetica), in Italia per indicare la posizione ordinale (specialmente i secoli e i pontefici), in musica nella numerazione dei gradi della scala diatonica e nella numerazione delle pagine delle prefazione dei libri. I numeri XV e XIII sono altresì usati per indicare le nazionali di rugby (15 e 13 come i giocatori schierati in campo nelle versioni union e league rispettivamente), mentre è diffuso, soprattutto nei paesi anglofoni, indicare talvolta con l'XI gli schieramenti di calcio, dove i giocatori sono infatti 11.
Il sistema numerico arabo è una notazione decimale posizionale.
Vari gruppi di simboli sono utilizzati per rappresentare i numeri del sistema numerico arabo e tutti sono evoluti dai numeri brahmi. I simboli utilizzati per rappresentare il sistema si sono divisi in varie varianti tipografiche sin dal Medioevo:
| Europeo (dall'arabo occidentale) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Indoarabo | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Indoarabo orientale (persiano e urdu) | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Devanagari (hindi) | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Tamil | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
Qui di seguito viene invece mostrata l'evoluzione della scrittura dei numeri arabi in Europa su una tabella redatta dallo studioso francese J. E. Montucla nella sua opera Histoire de la Mathématique (Storia della matematica), pubblicata nel 1758:
|
|
|
I numeri arabi sono codificati in ASCII (e in Unicode) nelle posizioni comprese tra 48 e 57:
| BIN | ASCII | HEX | Glifo |
|---|---|---|---|
| 0011 0000 | 48 | 30 | 0 |
| 0011 0001 | 49 | 31 | 1 |
| 0011 0010 | 50 | 32 | 2 |
| 0011 0011 | 51 | 33 | 3 |
| 0011 0100 | 52 | 34 | 4 |
| 0011 0101 | 53 | 35 | 5 |
| 0011 0110 | 54 | 36 | 6 |
| 0011 0111 | 55 | 37 | 7 |
| 0011 1000 | 56 | 38 | 8 |
| 0011 1001 | 57 | 39 | 9 |
LIMS forum content by LIMS forum members is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Based on a work at www.limsforum.com.
